the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Development of the WRF-CO2 4D-Var assimilation system v1.0
Nancy H. F. French
Martin Baxter
Regional atmospheric CO2 inversions commonly use Lagrangian particle trajectory model simulations to calculate the required influence function, which quantifies the sensitivity of a receptor to flux sources. In this paper, an adjoint-based four-dimensional variational (4D-Var) assimilation system, WRF-CO2 4D-Var, is developed to provide an alternative approach. This system is developed based on the Weather Research and Forecasting (WRF) modeling system, including the system coupled to chemistry (WRF-Chem), with tangent linear and adjoint codes (WRFPLUS), and with data assimilation (WRFDA), all in version 3.6. In WRF-CO2 4D-Var, CO2 is modeled as a tracer and its feedback to meteorology is ignored. This configuration allows most WRF physical parameterizations to be used in the assimilation system without incurring a large amount of code development. WRF-CO2 4D-Var solves for the optimized CO2 flux scaling factors in a Bayesian framework. Two variational optimization schemes are implemented for the system: the first uses the limited memory Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization algorithm (L-BFGS-B) and the second uses the Lanczos conjugate gradient (CG) in an incremental approach. WRFPLUS forward, tangent linear, and adjoint models are modified to include the physical and dynamical processes involved in the atmospheric transport of CO2. The system is tested by simulations over a domain covering the continental United States at 48 km × 48 km grid spacing. The accuracy of the tangent linear and adjoint models is assessed by comparing against finite difference sensitivity. The system's effectiveness for CO2 inverse modeling is tested using pseudo-observation data. The results of the sensitivity and inverse modeling tests demonstrate the potential usefulness of WRF-CO2 4D-Var for regional CO2 inversions.
- Article
(2560 KB) -
Supplement
(7836 KB) - BibTeX
- EndNote
While rising atmospheric CO2 has been well documented by observations, major uncertainties still exist in attributing it to specific processes (Gurney et al., 2002; Peylin et al., 2013). Atmospheric CO2 inversions estimate surface carbon fluxes from atmospheric CO2 measurements. Since the early study by Enting et al. (1995), a large amount of effort has been devoted to developing and applying atmospheric CO2 inversion methods. Most of these inversions are based on a Bayesian framework, and a wide range of different approaches has been used, including synthesis inversion (Rayner et al., 1999; Bousquet et al., 1999; Peylin et al., 2002; Gurney et al., 2002), geostatistical estimation (Michalak et al., 2004; Gourdji et al., 2012), Kalman smoother (Bruhwiler et al., 2005), ensemble Kalman smoother (Peters et al., 2005), and 4-D variational inversion (Chevallier et al., 2005; Baker et al., 2010). All of these inversion approaches are optimization systems which yield an optimal estimate of CO2 fluxes by minimizing a Bayesian cost function. Within these optimization systems, the observation vector is formed by atmospheric CO2 measurements, and the state vector is formed by CO2 fluxes and lateral boundary conditions (only for regional inversion systems). The relationship between CO2 fluxes and atmospheric CO2 is described by the influence function, which is also called the footprint or adjoint sensitivity. Because all of the inversion approaches use a chemistry–transport model (CTM) to relate CO2 fluxes to atmospheric CO2, the influence function in theory can be calculated by the CTM using a finite difference method. However, the practical limits imposed by computational costs often necessitate the aggregation of flux to reduce the state vector size, which leads to aggregation errors (Bocquet, 2009; Kaminski et al., 2001; Turner and Jacob, 2015). In practice, different inversion systems use different approaches to determine the influence function. Some inversion systems, including synthesis inversion, geostatistical estimation, and Kalman smoother, require the influence function to be explicitly constructed before the inversion. In comparison, the ensemble Kalman smoother and 4D-Var inversion do not require precalculation of the influence function. Precalculation of the influence function is typically carried out using a finite difference approach with the CTM when the state vector is smaller than the observation vector, or by the adjoint model of the CTM when the observation vector is smaller than the state vector. While most of the Lagrangian CTM models have their adjoint developed together (Uliasz, 1993; Lin et al., 2003; Stohl et al., 2005; Stein et al., 2015), separate and considerable efforts were often needed to develop and maintain the adjoint for Eulerian CTM models (Hourdin et al., 2006; Meirink et al., 2008). An ensemble Kalman smoother requires neither an adjoint model nor precalculation of the influence function. Instead it creates an ensemble of CO2 flux fields and runs a CTM for each ensemble member. By sampling the ensemble flux fields and their corresponding atmospheric CO2, the ensemble Kalman smoother calculates the Kalman gain matrix without explicitly constructing the influence function (Peters et al., 2005), and it provides posterior flux error estimates. The main disadvantage of the ensemble Kalman smoother is that use of a small number of ensemble members is likely to lead to misrepresentation of the true prior error variance.
Like ensemble Kalman smoothers, 4D-Var inversions do not require precalculation of the influence function, but they do require the adjoint of a CTM to calculate the observation cost function. 4D-Var inversions use a CTM and prior CO2 fluxes to calculate the simulated CO2, which is compared with observations to obtain the innovative vector. The adjoint of the CTM is then used to calculate the cost function gradient based on the innovative vector. Through iterative minimization of the cost function, 4D-Var inversions estimate the optimal posterior fluxes. By avoiding calculation of the influence function, 4D-Var inversions enable CO2 fluxes to be estimated at much higher resolution provided that sufficient observations are available. The major disadvantages of 4D-Var inversions are that they do not explicitly provide posterior flux error estimates (additional computation is required), and their convergence is not always guaranteed.
4D-Var systems have been widely used for CO2 inversion at global and regional scales. Examples of global 4D-Var inversions include the following. The offline transport model parameterized chemistry and transport model (PCTM) (Kawa et al., 2004) and its adjoint have been used for CO2 inversions (Baker et al., 2010, 2006; Butler et al., 2010; Gurney et al., 2005). Chevallier et al. (2005) developed a 4D-Var system based on the LMDZ (Laboratoire de Météorologie Dynamique-Zoom) model (Hourdin et al., 2006) to assimilate CO2 observation data from the Television Infrared Observation Satellite Operational Vertical Sounder (TOVS). This system has also been used to invert surface CO2 observations (Chevallier, 2007; Chevallier et al., 2010). The global chemistry–transport model (TM5) 4D-Var system (Meirink et al., 2008), based on the TM5 global two-way nested transport model (Krol et al., 2005), is included in the TransCom satellite intercomparison experiment (Saito et al., 2011). TM5 4D-Var has also been used to investigate total column CO2 seasonal amplitude (Basu et al., 2011) and to assimilate the Greenhouse Gases Observing Satellite (GOSAT) observations (Basu et al., 2013). Another widely used inversion system is the GEOS-Chem 4D-Var (Henze et al., 2007; Kopacz et al., 2009) with its CO2 module updated by Nassar et al. (2010). GEOS-Chem 4D-Var has been used to estimate CO2 fluxes from the Tropospheric Emission Spectrometer (TES) and the GOSAT CO2 observations (Nassar et al., 2011; Deng et al., 2014), and it is also part of the JPL (Jet Propulsion Laboratory) Carbon Monitoring System (Liu et al., 2014).
Regional 4D-Var inversion studies have been driven in part by the need to resolve biosphere–atmosphere carbon exchange at smaller scales (Gerbig et al., 2009), and by the need to address policy-relevant objectives, such as assessing emission reduction effectiveness (Ciais et al., 2014) and the impact of regional-scale sources like wildland fire (French et al., 2011). For instance, Gerbig et al. (2003) used an analytical approach to minimize the cost function and the Stochastic Time-Inverted Lagrangian Transport (STILT) (Lin et al., 2003) model driven by meteorological analyses to calculate the influence function. In a later study, STILT, driven by the European Centre for Medium-Range Weather Forecasts (ECMWF) meteorological data, is used to calculate the influence function to investigate the impacts of vertical mixing error (Gerbig et al., 2008). More recently, Lauvaux et al. (2012) also used an analytical solution for cost function minimization and the Lagrangian particle dispersion model (LPDM) (Uliasz, 1993) to compute the influence function. In another study, Pillai et al. (2012) used STILT driven by meteorological data from WRF to calculate the influence function for comparing Lagrangian and Eulerian models for regional CO2 inversions. To improve accuracy, STILT has been coupled to WRF, in which the latter provides online meteorology to STILT to avoid interpolation error (Nehrkorn et al., 2010). More recently, Alden et al. (2016) investigated biospheric CO2 flux in the Amazon using an analytical inversion approach (Yadav and Michalak, 2013) with the influence function calculated by STILT and FLEXible PARTicle (FLEXPART) (Stohl et al., 2005) models. Also, Chan et al. (2016) applied a regional CO2 inversion in Canada with both analytical and Markov chain Monte Carlo (MCMC) LPDM-based approaches. The influence function is also calculated with the FLEXPART model in this study.
In this paper, a regional CO2 inversion system with online meteorology, WRF-CO2 4D-Var, was developed by modifying the WRFDA and WRFPLUS system (v3.6) in an approach similar to that used for black carbon emission inversion by Guerrette and Henze (2015, 2017) (hereafter GH15/17). WRFDA is a meteorology data assimilation system which includes a 4D-Var assimilation system (Barker et al., 2012; Huang et al., 2009) and related adjoint and tangent linear models (WRFPLUS) (Zhang et al., 2013). Designed to improve weather forecasts, WRFDA 4D-Var optimizes meteorological initial and boundary conditions by assimilating a variety of observational data. WRFPLUS was modified to include CO2 transport processes and the cost function was configured so that the state vector consists of CO2 fluxes instead of meteorological fields. In developing WRFDA-Chem for black carbon inversion, GH15/17 excluded radiation, cumulus, and microphysics parameterization schemes from the tangent linear and adjoint models because developing these procedures for black carbon would incur a large amount of new code development. In WRF-CO2 4D-Var, CO2 is a tracer, meaning its impacts on meteorology are ignored. This configuration allows inclusion of the full physics schemes in WRF-CO2 4D-Var's tangent linear and adjoint models with limited new code development (see Sect. 2.4.1). As transport model error is detrimental to 4D-Var inversion accuracy (Fowler and Lawless, 2016; Gerbig et al., 2009), it is beneficial to use the full physics schemes in the tangent linear and adjoint models for WRF-CO2 4D-Var. In addition, while GH15/17 excluded convective transport of chemistry species in WRFDA-Chem, the tangent linear and adjoint code for this process was developed for WRF-CO2 4D-Var to reduce the vertical mixing error (see Sect. 2.4.3). Two optimization schemes were developed for WRF-CO2 4D-Var: an incremental optimization with the Lanczos version of the conjugate gradient (Lanczos-CG) and a limited memory Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization algorithm (L-BFGS-B)-based optimization.
In the WRF system, CO2 mixing ratio variations could impact meteorology fields through the radiation scheme, which provides temperature tendency to the dynamical core (Iacono et al., 2008; Skamarock et al., 2008). None of the radiation schemes (as of version 3.6) use the simulated CO2 from the chemistry module but instead use climatological values. A sensitivity test was conducted to assess the short-term impacts of CO2 variation on meteorology. The results show that with the CO2 mixing ratio changed from 391 to 500 ppm, the mean differences in horizontal wind (U, V) and air temperature at the end of the 48 h simulations are 0.0794 ms−1, 0.0791 ms−1, and 0.0366 K, respectively. Although these differences grow with time, their magnitudes are considerably smaller compared with the contribution from other factors for the short assimilation window (days to weeks) that WRF-CO2 4D-Var is designed for. Based on the above analysis, the impact of CO2 on meteorology is ignored in WRF-CO2 4D-Var, and CO2 is modeled as a passive tracer. This simplification allows WRF-CO2 4D-Var to use the full version of most WRF physics schemes in its tangent linear and adjoint models to minimize the linearization error (Tremolet, 2004).
Compared with offline regional inversion systems, WRF-CO2 4D-Var has an advantage provided by the close one-way coupling between meteorological processes and chemistry transport. For example, adequately representing CO2 vertical transport and eddy turbulent mixing in high-resolution regional simulations is crucial, as vertical motions in the atmosphere exhibit significant temporal variability. Grell et al. (2004) shows that less than 40 % of the total vertical velocity variability in a 3 km resolution simulation is captured by a 1 h output interval. He estimated that the meteorological output interval must be less than 10 min in order to capture more than 85 % of the variability in cloud-resolving simulations. In WRF-CO2 4D-Var, CO2 transport runs at the same time step as the meteorology, avoiding the problems facing its offline counterparts.
The remainder of this paper is organized as follows: Sect. 2 details the implementation of the two variational optimization schemes for cost function minimization, and the modification to the tangent linear and adjoint models. Section 3 examines the accuracy of sensitivity calculated by the tangent linear and adjoint models, and the system's effectiveness in inverse modeling. Section 4 describes the treatment of CO2 lateral boundary conditions in the WRF-CO2 4D-Var system. Finally, a summary and outlook are presented in Sect. 5.
This section describes the WRF-CO2 4D-Var cost function configuration and the associated minimization schemes, followed by a description of the forward, tangent linear, and adjoint models.
2.1 Cost function configuration
WRF-CO2 4D-Var is designed to optimize the CO2 flux by assimilating CO2 observations into an atmospheric chemistry transport model. The CO2 flux is optimized through use of a linear scaling factor:
where is the CO2 flux read from flux files, kco2 is the flux scaling factor, and E is the effective CO2 flux. It is the effective flux E that is used in WRF-Chem's emission driver to update CO2 mixing ratio (qco2). The flux scaling factor kco2, its tangent linear variable g_kco2, and its adjoint variable a_kco2 are used in calculating model sensitivity and minimizing the cost function defined in Eq. (2).
The cost function J(x) of WRF-CO2 4D-Var follows the Bayes framework that is widely used in atmospheric chemistry and numerical weather prediction (NWP) data assimilations:
where the background cost function Jb(x) is defined as
and the observation cost function Jo(x) is defined as
In Eqs. (3)–(4), B is the background error covariance matrix, R is the observation error covariance matrix, M is the transport model, H is the observational operator, yk is the observation vector, and xb is the prior state vector. The superscript n indicates that xn is the optimized state vector at the nth iteration. For a full list of variables used in this paper, please refer to Table 1. Throughout the paper, boldface lowercase characters represent vectors and boldface uppercase characters represent matrices.
Like other data assimilation systems, WRF-CO2 4D-Var is an optimization scheme. Its state vector x consists of the flux scaling factors kco2 and lateral boundary condition scaling factors. The summation K in Eq. (4) indicates the entire assimilation time period is evenly split into K observation windows during which observational data are ingested into the assimilation system. Details about how observations are ingested in the variational optimization schemes are given in Sect. 2.2 and 2.3.
Two optimization schemes are implemented in WRF-CO2 4D-Var to minimize the cost function. The first scheme uses the L-BFGS-B algorithm (Byrd et al., 1995) and the second uses the Lanczos-CG (Lanczos, 1950) minimization algorithm. Both schemes are iterative processes, and they call on WRF-CO2 4D-Var model components (the forward, tangent linear, and adjoint models) to calculate the model sensitivity between the iterations. The two optimization schemes are described in Sect. 2.2 and 2.3, respectively, and the three model components are described in Sect. 2.4.
2.2 L-BFGS-B optimization
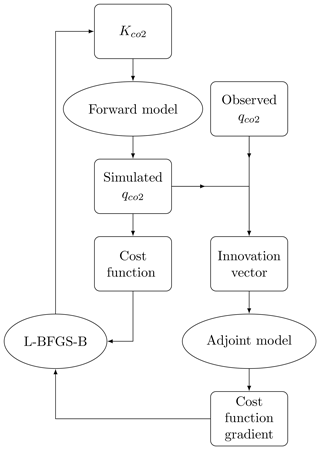
L-BFGS-B (Byrd et al., 1995) is a quasi-Newton method for nonlinear optimization with bound constraints. L-BFGS-B has been used in a number of atmospheric chemistry inverse modeling systems, including the GEOS-Chem adjoint model system (Henze et al., 2007) and the TM5 4D-Var system (Meirink et al., 2008). The diagram in Fig. 1 demonstrates the steps involved in the L-BFGS-B-based optimization scheme. The scheme is an iterative process which searches for the optimized kco2 by minimizing the cost function defined in Eq. (2)–(4). Between its iterations, the minimization algorithm L-BFGS-B requires the values of the cost function and its gradient, which are supplied by the forward model and the adjoint model as indicated in Fig. 1.
The calculation of the cost function is carried out based on Eqs. (2)–(4). Starting with the prior estimate of kco2, the forward model run generates the CO2 mixing ratio qco2, which is transformed from the WRF model space to the observation space by the forward observation operator H. This results in the H(M(xn)) term in Eq. (4), which is then paired with the observation vector yk to calculate the innovation vector . Next, the innovation vector and observation error covariance R are used to calculate the observation cost function Jo(x) as expressed in Eq. (4). Finally, the background cost function Jb(x) is calculated according to Eq. (3) and combined with the observation cost function Jo(x) to form the total cost function J(x) according to Eq. (2).
L-BFGS-B requires the values of the cost function J(x) and its gradient ∇ J(x) in searching for the optimized kco2. The gradient is calculated using Eq. (5).
The first term on the right-hand side of Eq. (5) is the observation gradient and the second is the background gradient. The observation gradient is calculated in two steps. (1) The innovation vector is scaled by R−1 and transformed to the WRF model space by the adjoint observation operator, resulting in , which is the adjoint forcing. (2) The adjoint forcing is then ingested by the WRF-CO2 adjoint model during its backward (in time) integration, which yields the observation gradient. Supplied with the values of the cost function and gradient, the L-BFGS-B algorithm finds a new value of kco2, which is used for the next iteration. The iterative optimization process continues until a given convergence criterion is met. The L-BFGS-B-based optimization in WRF-CO2 4D-Var is implemented based on the Fortran code of Algorithm 788 version Lbfgsb.2.1 (Zhu et al., 1997). Version Lbfgsb.3.0 (Luis Morales and Nocedal, 2011) will be implemented in the next model update.
2.3 Incremental optimization
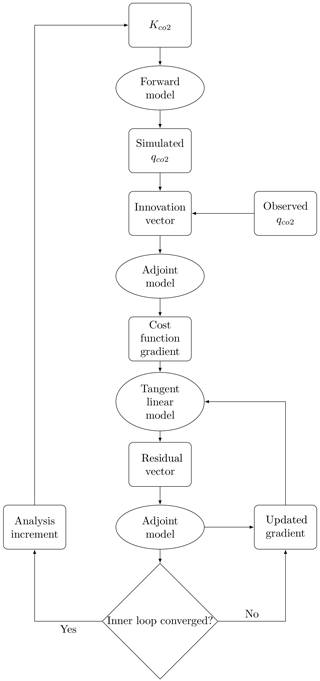
The second optimization scheme implemented for WRF-CO2 4D-Var is the incremental approach commonly used in NWP data assimilation systems, including ECMWF 4D-Var (Rabier et al., 2000) and WRFDA (Barker et al., 2012). A major difference between the L-BFGS-B-based optimization and the incremental optimization is that the former optimizes for the state vector while the latter optimizes for the state vector analysis increment. The incremental assimilation scheme uses a linear approximation to transform the observation cost function from what is defined in Eq. (4) to Eq. (6):
Compared to Eq. (4), Eq. (6) approximates the innovation vector by a sum of two parts. The first part, , is the innovation vector from the previous iteration. The second part, , is the state vector analysis increment transformed by the tangent linear model and tangent linear observation operator . With the linear approximation of the cost function the gradient is calculated by
In WRF-CO2 4D-Var, the incremental optimization is implemented as a double loop in which the outer loop calculates the first and second items on the right-hand side of Eq. (7), while the inner loop calculates the third and fourth items. The superscript n−1 indicates that xn−1 is the optimized state vector in the last outer loop, and superscript n indicates that xn is the optimized state vector in the inner loop. The outer loop first calls the forward model M and adjoint model to calculate and , which remain unchanged during the subsequent inner loop calculation. The analysis increment is optimized in the inner loop, which calls the tangent linear and adjoint models to calculate the third and fourth items of Eq. (7). Inner loop calculation is carried out by Lanczos-CG (Lanczos, 1950), which can optionally estimate eigenvalues of the cost function Hessian matrix (∇2 J(x)). The diagram in Fig. 2 shows the structure of the Lanczos-CG-based incremental optimization implemented in WRF-CO2 4D-Var.
2.4 Forward, tangent linear, and adjoint models
WRFPLUS consists of three model components: the WRF model, its tangent linear model, and its adjoint model (Barker et al., 2012; Huang et al., 2009). The three models are used by WRFDA to optimize the initial meteorological condition in order to improve numerical weather prediction. Unlike WRFDA, WRF-CO2 4D-Var is designed to optimize the CO2 flux, instead of the meteorological initial and boundary conditions. This difference means the physical and dynamical processes involved in the atmospheric CO2 transport are needed in WRF-CO2 4D-Var's model components. To include these processes, the chemistry module was added to the forward model. The chemistry module includes chemistry, deposition, photolysis, advection, diffusion, and convective transport of chemistry species (Grell et al., 2005). These processes are included in different modules of WRF-Chem: ARW (Advanced Research WRF) dynamical core, physics driver, and chemistry driver. The GHG (greenhouse gas) tracer option was removed and CO2 is treated as an inert tracer. In the emission driver, the CarbonTracker 2016 version (Peters et al., 2007) replaces the online biogenic CO2 model Vegetation Photosynthesis and Respiration Model (VPRM) (Mahadevan et al., 2008). This change is made because WRF-CO2 4D-Var optimizes the CO2 flux instead of online emission model parameters.
2.4.1 Variable dependence analysis
The tangent linear and adjoint models of WRFPLUS needed to be modified to include the physical and dynamical processes involved in the atmospheric transport of CO2, so that they will be consistent with the forward model. A thorough variable dependence analysis was conducted and the results are summarized in Table 2, which groups WRF-Chem processes into three categories regarding CO2 tracer transport. The first category includes the chemistry processes that do not apply to CO2, including gas- and aqueous-phase chemistry, dry and wet deposition, and photolysis. These processes are simply excluded from the forward, tangent linear, and adjoint models in WRF-CO2 4D-Var.
The second category is comprised of the physical parameterizations that do not provide CO2 tendency but provide meteorological tendency. This category includes radiation, surface, cumulus, and microphysics parameterizations. While the full physics schemes of surface, cumulus, planetary boundary layer (PBL), and microphysics are used in the forward model of WRFPLUS, simplified versions of these schemes are used in its tangent linear and adjoint models. In addition, WRFPLUS uses full radiation schemes (longwave and shortwave) in its forward model, but it excludes radiation schemes from its tangent linear and adjoint models. The difference in the physical parameterizations between the forward model and tangent linear/adjoint models in a 4D-Var system is a source of linearization error. For instance, Tremolet (2004) found linearization error in ECMWF 4D-Var larger than expected and recommended more accurate linear physics for higher resolution 4D-Var systems. Because WRF-CO2 4D-Var ignores the impacts of CO2 mixing ratio variation on the meteorological fields, no tangent linear and adjoint variables for meteorological fields are needed in its tangent linear and adjoint models. Since this second category of processes is not directly involved in CO2 transport, there is no need for their tangent linear and adjoint procedures in WRF-CO2 4D-Var. In WRFPLUS's tangent linear model, the tangent linear code of the simplified versions of the cumulus, surface, and microphysics schemes was removed and replaced with the code for the full schemes as used in the forward model. In WRFPLUS's adjoint model, the forward sweep updates the state variables and local variables just as in the forward model, but it also stores these variables' values for the subsequent backward sweep, which updates the adjoint variables of the state variables. The simplified versions of the cumulus, surface, and microphysics schemes used in the forward sweep of WRFPLUS's adjoint model were removed and replaced with the full schemes used in the forward model. Since these processes do not directly modify CO2 mixing ratio, their corresponding adjoint code was removed from the backward sweep of the adjoint model, as indicted by the “X” in Table 2.
Table 2Summary of variable dependence analysis for developing WRF-CO2 4D-Var component models on top of WRFPLUS. In the table, an “F” means a full physics scheme is used in the forward model, tangent linear model, or the forward sweep of the adjoint model. An “X” means a process is not needed for CO2 treatment. A “Dev” means a process does not exist in WRFPLUS and has been developed for WRF-CO2 4D-Var. An “Add” means a process for CO2 is simply added using the existing WRFPLUS code for other tracers.
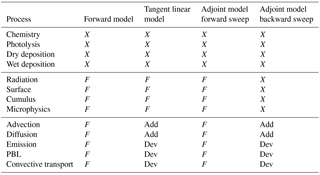
The third category includes advection, diffusion, emission, and turbulence mixing in the PBL, along with convective transport of CO2. Because these processes directly modify CO2 mixing ratio, their tangent linear code and adjoint code are needed for WRF-CO2 4D-Var. The modifications made for advection and diffusion are described in Sect. 2.4.2, and those for emission, turbulent mixing in the PBL, and convective transport of CO2 are detailed in Sect 2.4.3.
2.4.2 Advection and diffusion of CO2
WRF includes the advection and diffusion of inert tracers along with other scalars in its ARW dynamical core. The tangent linear and adjoint code for these processes has been implemented in WRFPLUS. It should be noted that the variables for these inert tracers are part of WRF, instead of WRF-Chem. WRF-Chem uses a separate array for its chemistry species. Since WRF-Chem is used as the forward model of WRF-CO2 4D-Var, the CO2 mixing ratios are included in the chemistry array. In the GHG option of WRF-Chem used for WRF-CO2 4D-Var, CO2 from different sources (anthropogenic, biogenic, biomass burning, and oceanic) is represented by separate variables in the chemistry array. Following the treatment for the inert tracers in WRFPLUS, subroutines solve_em_tl and solve_em_ad were modified to add the tangent linear and adjoint code for the advection and diffusion of the chemistry array. The modifications made include adding calls to the procedures that calculate advection and diffusion tendencies, updating the chemistry array with the tendencies and boundary conditions, and addressing the Message Passing Interface (MPI) communications. The new upgrade to WRFPLUS described in Zhang et al. (2013) greatly expedited this part of development for WRF-CO2 4D-Var. The “Add” in Table 2 for advection and diffusion emphasizes that their tangent linear and adjoint code is added to WRF-CO2 4D-Var based on the existing WRFPLUS code without substantial new code development.
2.4.3 Vertical mixing of CO2 in PBL and convective transport
An accurate representation of vertical mixing is important for inversion accuracy, because misrepresentation causes transport error, which manifests itself in the innovation vector and causes error in posterior estimation (Fowler and Lawless, 2016). For instance, Stephens et al. (2007) pointed out that global chemistry transport model error in vertical mixing and boundary layer thickness could cause significant overestimation of northern terrestrial carbon uptake. A comparison of four global models found that model transport uncertainty exceeds the target requirement for the A-SCOPE mission of 0.02 Pg C yr−1 per 106 km2 (Houweling et al., 2010). In addition, Jiang et al. (2008) reported that convective flux is likely underestimated in boreal winter and spring based on simulated upper tropospheric CO2 from 2000 to 2004 using three chemistry transport models.
In WRF-Chem, vertical mixing of chemical species is treated in three separate parts: in the vertical diffusion (subgrid-scale filter) in the dynamical core, in the PBL scheme in the physics driver, and in the convective transport in the chemistry driver. The subgrid-scale filter in the dynamical core treats both horizontal and vertical diffusion, but vertical diffusion is turned off if a PBL scheme is used.
For PBL parameterization, the asymmetrical convective model version 2 (ACM2) (Pleim, 2007) was chosen for WRF-CO2 4D-Var. ACM2 is a hybrid local–non-local closure PBL scheme, and it updated the non-local scheme, ACM1 (Pleim and Chang, 1992), by adding an eddy diffusion component. Because ACM2 explicitly defines local and non-local mass fluxes, it is particularly applicable for atmospheric chemistry simulations. In a one-dimensional model evaluation, ACM2 showed a very good agreement with large-eddy simulations for PBL heights with a very slight low bias (Pleim, 2007). In addition to WRF, ACM2 has been implemented in the fifth-generation Penn State/National Center for Atmospheric Research (NCAR) Mesoscale Model (MM5) and the Community Multiscale Air Quality (CMAQ) model. An evaluation using PBL heights derived from radar wind profiles showed that the MM5-ACM2 is capable of realistic simulation of PBL heights (Pleim, 2007). Hu et al. (2010) evaluated three WRF PBL schemes and found that ACM2 resulted in less bias than the local closure Mellor–Yamada–Janjić (MYJ) scheme when compared with surface and boundary layer observations. Furthermore, model evaluations also showed that ACM2 performed well with CMAQ for air pollution simulations (Nolte et al., 2015; Appel et al., 2017).
Convective transport of chemistry species in WRF-Chem is not treated by the cumulus scheme in the physics driver but by a separate convective transport module (module_ctrans_grell) in the chemistry driver (Grell et al., 2004). This convective transport module includes a deep convective process and a shallow convective process. The deep convective transport process requires the convective precipitation rate calculated by the cumulus scheme (in the physics module of WRF): it calculates the base mass flux based on the convective precipitation rate. Compared to the ensemble stochastic approach used in the Grell–Freitas cumulus scheme (Grell and Freitas, 2014), this is a rather crude representation of the vertical convective transport. The shallow convective process requires three parameters passed in from the cumulus scheme in the physics module: updraft originating level, cloud top level, and total base mass flux. Only two cumulus schemes in WRF provide these parameters: the Grell–Freitas (Grell and Freitas, 2014) and Grell 3D Ensemble (Grell and Devenyi, 2002).
Because the ACM2 PBL and chemistry convective transport are not included in WRFPLUS, their tangent linear and adjoint code was developed for WRF-CO2 4D-Var. First, the automatic differentiation tool Tapenade (Hascoet and Pascual, 2013) was used to generate the tangent linear and adjoint code based on the forward code: module_bl_acm for the ACM2 PBL and module_ctrans_grell for the chemistry convective transport. Then, the Tapenade-generated code was manually modified to remove redundancy and unnecessary loops. It should be pointed out that these code developments were made significantly simpler because the meteorological state variables are merely passive variables in the tangent linear and adjoint code. For instance, to calculate the moist static energy and environmental values on cloud levels, the chemistry convective transport code (module_ctrans_grell) in the chemistry driver calls a number of subroutines in the cumulus parameterization code in the physics driver. Because these subroutines in the cumulus parameterization only involve meteorology state variables and not the chemistry array, no tangent linear or adjoint code is needed for them in WRF-CO2 4D-Var.
This section presents an accuracy assessment of the newly developed WRF-CO2 4D-Var system. First, the simulation model setup is described; then, the sensitivity tests and inverse modeling experiments are presented.
3.1 Model setup
WRF-CO2 4D-Var is set up with a domain covering the continental United States with 48 km × 48 km grid spacing and 50 vertical levels (Fig. 3). The domain dimension is 110 points in the east–west and 66 points in the north–south directions. Model configuration includes the Rapid Radiative Transfer Model (RRTM) longwave radiation (Mlawer et al., 1997), Goddard shortwave radiation (Chou and Suarez, 1999), Pleim surface layer (Pleim, 2006), Pleim–Xiu land surface model (Pleim and Xiu, 2003), ACM2 PBL (Pleim, 2007), Grell–Freitas cumulus (Grell and Freitas, 2014), and Thompson microphysics (Thompson et al., 2008). Positive–definite transport is applied to the transport of scalars and CO2.
CO2 fluxes used for the simulations are from the CarbonTracker 2016 version (hereafter CT2016) (Peters et al., 2007). These fluxes are the optimized surface fluxes at a 3 h interval and at 1×1 degree spatial resolution. The four individual CO2 fluxes (biosphere, fossil fuel, fire, and ocean) are spatially interpolated to the WRF grid and saved in chemistry input files. In the following sensitivity tests and inverse experiments, the emission scaling factor kco2 is applied only to the biosphere flux. Daily mean biospheric fluxes are calculated as the arithmetic mean of the 3-hourly CT2016 fluxes at each surface grid cell, and the scaling factor kco2 is applied as in Eq. (1). The daily mean biospheric flux used for the 24 h simulation is shown in Fig. 4. The model configuration and emission data used are summarized in Table 3. Although the daily mean biospheric flux was used for the forward and inverse modeling in this paper, the WRF-CO2 4D-Var implementation allows flexibility in configuring the prior fluxes. For instance, fluxes from respiration and photosynthesis can be estimated independently and at higher temporal resolution (Gourdji et al., 2012). When using these options with real observations, the balance between the degrees of freedom in the state vector and the constraints provided by the observations needs to be carefully considered.
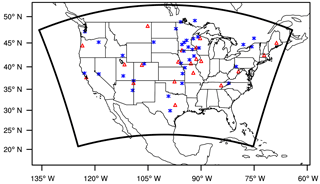
Figure 3WRF 4D-Var simulation domain covering the continental United States with 48 km × 48 km grid spacing. The domain boundary is marked by the bold dark outline. Grid cells used for evaluating sensitivities are marked: red triangles are the 20 CO2 tower sites used as receptor locations; blue stars are source locations. While receptors are placed at the first, fifth, and tenth vertical levels at each site; all sources are at the first level only.
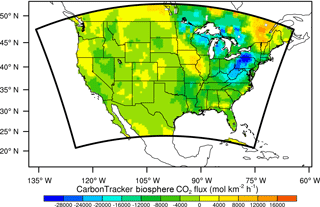
Figure 4Daily mean CarbonTracker biosphere CO2 flux, calculated as the arithmetic mean of the 3-hourly flux between 2 June 2011 at 00:00:00 UTC and 3 June 2011 at 00:00:00 UTC.
Model simulations span 24 h from 00:00 UTC on 2 June to 00:00 UTC on 3 June 2011. Meteorological initial and lateral boundary conditions are prepared using the National Centers for Environmental Prediction (NCEP) Climate Forecast System version 2 (CFSv2) 1×1 degree 6-hourly products (Saha et al., 2014). CO2 initial and lateral boundary conditions are from the CT2016 global 3×2∘ CO2 mole fraction. A method similar to PREP-CHEM-SRC (Freitas et al., 2010) was used to horizontally and vertically interpolate CT2016 mole fraction data to the WRF grid.
Table 3WRF-CO2 4D-Var model configuration and CO2 flux used in sensitivity and inverse modeling tests.

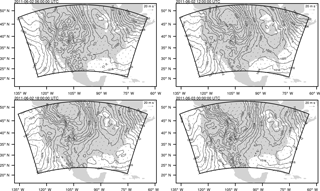
Figure 5Sea level pressure (hPa) and horizontal wind (m s−1) at the model's lowest vertical level plotted at 6 h intervals during the 24 h simulation starting on 2 June 2011 at 00:00 UTC.
First, the forward model (WRF-Chem) was run for 24 h with the CO2 emission as described in the last section. Trajectory files that contain model state variables including both meteorology and CO2 mixing ratio are saved at model dynamical time step intervals (120 s). These files are required for the subsequent tangent linear and adjoint model runs. Figure 5 shows the instantaneous values of sea level pressure (SLP) and horizontal wind at the model's lowest vertical level at every 6 h. The figure shows that a high pressure system was located off the west coast, causing a northerly surface wind off southern California, and a westerly wind for most of the Pacific Northwest. A low pressure system intensified over Montana and North Dakota during the 24 h, causing a strong southerly wind over the Midwest. In the northeast, as a low pressure system moved eastward out of the domain, the surface wind shifted from southwesterly to westerly.
In the model setup, the initial and boundary meteorological conditions are generated by downscaling the CFSv2 data. Downscaling coarse-resolution global reanalysis data could lead to poor WRF performance. Although this potential problem is not a concern for the present pseudo-observation-based inversion experiments, it must be properly treated in future applications with real observations. Error in the initial condition will lead to erroneous flux attribution, especially for inversions with a short assimilation window.
In order to be useful for applications which employ real observational data, WRF-CO2 4D-Var requires accurate simulations of the meteorological fields by the forward model. Because transport error can only be partially accounted for in the 4D-Var system through the observation error covariance matrix, it is imperative to minimize errors due to inaccurate simulation of meteorological processes as much as possible. Although the present paper uses pseudo-observation data (which have zero transport error by definition) in its inversion experiments, future applications with real observations will require vigorous evaluation of the model-simulated meteorology and associated transport error. In the following, the forward-model-simulated horizontal winds at the surface and 500 hPa constant pressure surface are evaluated using in situ measurements from weather stations and radiosondes.
For the surface level, WRF-simulated 10 m winds are compared against surface weather station measurements archived in the National Oceanic and Atmospheric Administration (NOAA) Integrated Surface Database (Smith et al., 2011). Hourly surface wind measurements from more than 2000 stations within the WRF domain are used for the evaluation. Comparisons of wind speed and wind direction are carried out at the top of each hour during the 24 h simulation period starting at 00:00 UTC on 2 June 2011. Excluding missing observations, this results in 31 745 valid data pairs, which are summarized in the histograms of Fig. 6. RMSE for the hourly wind speed is 2.16 m s−1 and the mean difference in the hourly wind direction is 29.4∘.
For the upper level, WRF-simulated 500 hPa horizontal winds were compared against radiosonde measurements from 90 stations obtained from the NOAA Earth System Research Laboratory (ESRL) radiosonde database (https://ruc.noaa.gov/raobs/, last access: 27 April 2018). Since most stations release balloons at 00:00 and 12:00 UTC, WRF winds were compared against the radiosonde measurements at a 12 h interval during the 24 h simulation period. The results are shown in Fig. 7: RMSEs of wind speed are 2.54, 4.0, and 5.11 m s−1, on 2 June at 00:00 UTC, 2 June at 12:00 UTC, and 3 June at 00:00 UTC, respectively. Wind direction differences between WRF and radiosonde are 11.5, 16.4, and 19.1∘ at the three times. Locations of the weather stations and radiosonde sites used in the evaluations can be found in the Supplement.
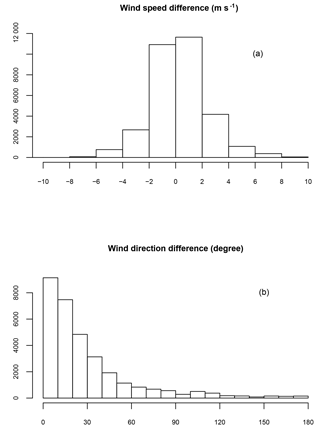
Figure 6Histograms of the 10 m wind speed difference (a) and wind direction difference (b) between the WRF simulation and surface meteorological station measurements.
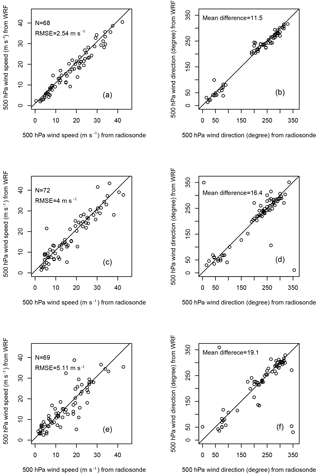
Figure 7Comparison of 500 hPa wind speed and wind direction between WRF simulation and radiosonde measurements. Panels (a) and (b) are the comparison on 2 June 2011 at 00:00 UTC; panels (c) and (d) are on 2 June 2011 at 12:00 UTC; and panels (e) and (f) are on 3 June 2011 at 00:00 UTC. RMSE and relative error (RE) for wind speed and mean difference in wind direction are shown in each figure.
The above-described evaluations using in situ measurements indicate that the meteorological simulation is of adequate accuracy for the pseudo-observation-based inverse modeling tests conducted in this paper. When the 4D-Var system is applied with real observations, the error and bias must be considered. In WRF 4D-Var's cost function configuration, the observation error matrix R is a combination of three error sources: measurement error, aggregation error, and transport model error. The uncertainty of the CO2 measurements is about 0.05 %, while the transport and aggregation errors are typically an order of magnitude larger (Bruhwiler et al., 2005). For real observation applications, the variance and covariance in R need to represent the transport error. Furthermore, Fig. 6 shows that WRF-simulated 10 m wind speed is biased high, which is likely to result in bias in the simulated atmospheric CO2 mixing ratio. Because Bayes inversion framework assumes unbiased observation error, it may be imperative to correct the error for inversions. One approach is to nudge the meteorology fields toward the observations. For instance, Gupta et al. (1997) found that nudging the model-simulated winds in the boundary layer to the radar wind profile observations substantially improved estimates of plume dispersion. An alternative approach is to use a combined 4D-Var inversion of meteorology and CO2 fluxes. For instance, Bocquet et al. (2015) discussed data assimilation using coupled chemistry meteorology models (CCMMs). If the CO2 impact on meteorology is not considered, the current implementation of WRF-CO2 4D-Var can be extended to a joint meteorology and CO2 assimilation system. Since the adjoint code for meteorology has been developed and tested in WRFPLUS and WRFDA (Zhang et al., 2013; Barker et al., 2012), the major modification would be in the optimization schemes where the combined state vector of meteorology and CO2 is optimized. It should be noted that in such a joint assimilation framework, optimization of meteorology is an initial condition problem, whereas the CO2 flux optimization is a boundary condition problem (bottom and lateral boundaries).
3.2 Accuracy of tangent linear and adjoint sensitivities
Next, the accuracy of the newly developed tangent linear and adjoint models was evaluated by comparing their sensitivity calculations against finite difference sensitivity calculated by the forward model. Grid cells involved in the sensitivity calculations are shown in Fig. 3, in which the 35 blue stars are the source cells, and the 20 red triangles are 20 tower sites where the receptors are placed (Table 4). All the 35 sources are placed at the grid's bottom vertical level. Receptors are placed at the first, fifth, and tenth vertical levels at each of the 20 tower sites, resulting in 60 receptor cells.
A tangent linear model run for a grid cell will calculate the tangent linear sensitivity , which approximates a column vector of the forward model's Jacobian matrix and quantifies the influence of the cell's flux change on CO2 mixing ratio of its receptor cells downwind. In comparison, an adjoint model run for a grid cell will calculate adjoint sensitivity , which approximates a row vector of the forward model's Jacobian matrix and quantifies the influence on the cell's CO2 mixing ratio by its source cells upwind. Because kco2 multiplies emission in Eq. (1), the magnitude of the sensitivity is determined by both the magnitude of emission and meteorological transport.
To calculate tangent linear sensitivity at a grid cell, g_kco2 is set to unity at the cell and zero at all other cells at the start of a tangent linear model run. Upon completion, the values of g_qco2 are the tangent linear sensitivities . To calculate adjoint sensitivity at a cell, an adjoint model run starts with a_qco2 set to unity at the cell and zero at all others, and the values of a_kco2 at the end of the simulation are the adjoint sensitivities. The adjoint model running in this mode is analogous to using a Lagrangian particle transport model in backward trajectory mode to compute the footprint of a receptor, as shown in Fig. 4 of Gerbig et al. (2008).
The tangent linear sensitivity is first compared against the finite difference sensitivity. After confirming the accuracy of the tangent linear model, the adjoint sensitivity is compared against the tangent linear sensitivity. Finite difference sensitivities are calculated using the two-sided formula (Eq. 8).
The magnitude of Δx used in Eq. (8) is determined by comparing the result from a range of different values. The finite sensitivities were calculated at the 35 sites using Δx set to 0.01, 0.1, and 1.0, and the results show that the magnitude of all differences is less than 10−10 (results not shown) because WRF-CO2 is largely linear. For all subsequent calculations, Δx=0.1 is used for Eq. (8).
Since both finite difference and tangent linear sensitivities form columns of the Jacobian matrix, their values can be compared cell by cell for all receptor cells for a given site. Figure 8 shows the comparison between the finite difference and tangent linear sensitivities at 9 of the 35 source cells. The dark straight lines in the figures are the 1 : 1 line. The maximum and minimum of the difference between finite difference and tangent linear sensitivities are given for each source cell. Results at the rest of the sources are similar (not shown). All differences are less than 10−10, confirming that the tangent linear model is accurate.

Figure 8Comparison between calculated by finite difference (x axis) and tangent linear models (y axis) for nine source cell locations (see Fig. 3 for source locations).
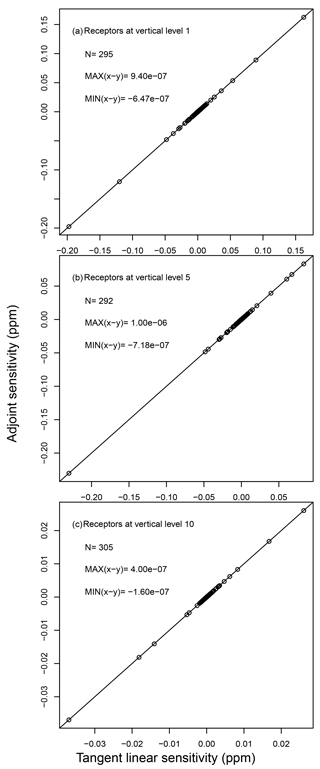
The adjoint model is next evaluated by comparing adjoint sensitivities against the tangent linear sensitivities. Because finite difference sensitivities form columns of the Jacobian matrix while adjoint sensitivities form rows of the Jacobian matrix, they can only be compared at the intersections of the rows and columns of the Jacobian matrix, meaning there are 2160 (35×60) pairs of comparison. We organized these 2160 pairs into three groups based on the vertical levels a receptor is placed at and the result is shown in Fig. 9. The minimum and maximum value of the difference between tangent linear and adjoint sensitivities in all three groups are no greater than 10−6, which is comparable to the accuracy tests from other adjoint model developments (Meirink, 2008; Henze, 2007), indicating that the adjoint model has been correctly implemented.
3.3 Spatial patterns of adjoint sensitivities
Adjoint sensitivity qco2∕kco2 quantifies how qco2 of a given receptor is impacted by the flux scaling factor of all surface cells. It is similar to the receptor footprint typically calculated using LPDM, such as Fig. 4 of Gerbig et al. (2008) and Fig. 1 of Alden et al. (2016). But qco2∕kco2 differs from footprint in that the former contains the combined impact of tracer transport and flux magnitude, while the latter is determined by tracer transport alone. The spatial patterns of the adjoint sensitivity were examined to discern the impacts of tracer transport. Figure 10 shows qco2∕kco2 of Centerville, Iowa (top row), and WLEF (tower at Park Fall), Wisconsin (bottom row). At each tower site, qco2∕kco2 of the receptor placed at the first and tenth vertical levels is plotted.
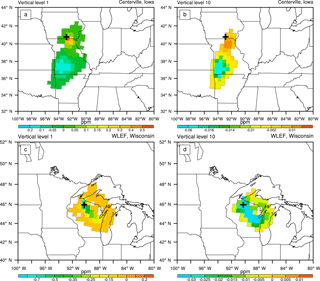
Figure 10Adjoint sensitivities calculated by the WRF-CO2 adjoint model. The top panels show adjoint sensitivity of receptors placed at the first (a) and tenth (d) vertical levels at Centerville, Iowa. The bottom panels show adjoint sensitivity of receptors placed at the first (c) and tenth (d) vertical levels at WLEF, Wisconsin. The black cross in each figure marks the corresponding tower site.
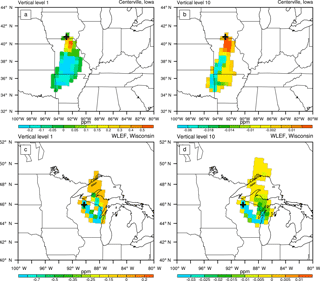
Figure 11Footprints calculated using Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) backward trajectories and CarbonTracker biospheric fluxes for the tower sites at Centerville, Iowa, and WLEF, Wisconsin. The receptor locations are the same as in Fig. 10. Each HYSPLIT footprint is plotted in the same color scale as its counterpart in Fig. 10 for comparison.
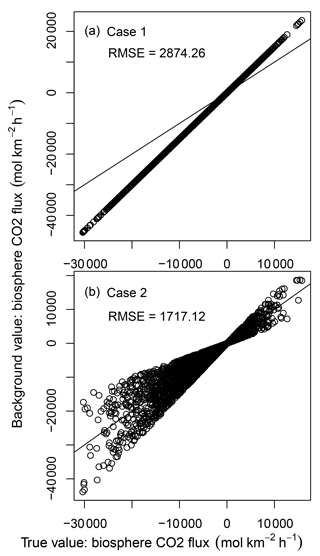
Figure 12The first-guess biosphere CO2 fluxes used in the two inverse modeling experiments. The x axis is the true daily mean CarbonTracker biosphere CO2 value (as shown in Fig. 4), and the y axis is the first guess (background value). The solid line in each figure is the 1 : 1 line.
The adjoint sensitivities of the Centerville tower site indicate its qco2 results primarily from surface flux located immediately south of the site. This pattern agrees with the fact that low-level wind during the simulation period is predominantly southerly, transporting tracers northward. There is also a marked difference in the adjoint sensitivity of the same tower site when the receptor is placed at a different height. The figure in the top left panel of Fig. 10 shows that the highest magnitude of qco2∕kco2 is closest to the tower itself, indicating a large impact from local fluxes. In comparison, when the receptor is placed at the tenth vertical level, the peak magnitude of its adjoint sensitivity is located further south of the tower site. Results from the WLEF site show the adjoint sensitivity is located to the southeast of the site, matching the southeasterly wind patterns around Wisconsin during the simulation period. There are also clear difference between the receptors at the different vertical levels. Results from other sites all show a similar pattern of impacts of transport and receptor placement height (not shown).
To provide a comparative view of the source–receptor relations, backward trajectories of particles released from the Centerville and WLEF sites were also calculated using the Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) model (Stein et al., 2015). WRF-CO2 forward-model-simulated meteorology saved at 1 h intervals was used to drive the HYSPLIT trajectory calculations. To compare with the adjoint model result, two sets of simulations were carried out for each of the two tower sites. For each simulation, 30 000 particles were released from the location of the corresponding WRF grid box used in the adjoint sensitivity calculations. The starting locations of the particles were randomly distributed within the grid box. The resulting backward trajectories were combined with the biospheric CO2 flux to calculate the footprint for the receptor locations. The HYSPLIT footprints were calculated on the same grid as used in the WRF-CO2 simulations to facilitate the comparisons between the two models.
Figure 11 shows the HYSPLIT-calculated footprints for the Centerville and WLEF sites at the two different vertical levels. The four figures in Fig. 11 are the HYSPLIT counterparts of the adjoint sensitivity figures in Fig. 10. A comparison between Figs. 10 and 11 shows that the results from HYSPLIT and the WRF-CO2 adjoint model compare well spatially. For instance, for the receptor placed at the first vertical level at Centerville, Iowa (Figs. 10a and 11a), the footprints from both models are primarily located in Missouri and northwestern Arkansas. Based on the horizontal wind fields at the first level, these areas were upwind of the receptor location during the simulation period. Overall, the WRF-CO2 adjoint sensitivities contain larger surface areas compared to their HYSPLIT footprint counterparts. This difference is likely caused by the more diffusive nature of tracer transport in WRF-CO2: its finite difference scheme for tracer advection contains numerical diffusion, and it also includes an explicit horizontal diffusion term in the tracer transport (Skamarock et al., 2008). A further comparison at individual grid points reveals magnitude differences between the footprints from HYSPLIT and the WRF-CO2 adjoint model. This is mainly caused by the different treatments of turbulent vertical mixing by the two models. In WRF-CO2, the PBL and convective schemes parameterize tracer vertical mixing (see Sect. 2.4.3). For vertical mixing, HYSPLIT either uses the PBL heights calculated by WRF or it calculates PBL heights independently by analyzing temperature profiles. The footprints shown in Fig. 11 were simulated by HYSPLIT using PBL heights from the WRF-CO2 ACM2 PBL scheme. In a separate set of HYSPLIT simulations with PBL heights calculated from the temperature profiles, only minor differences are observed in the resulting footprints (not shown).
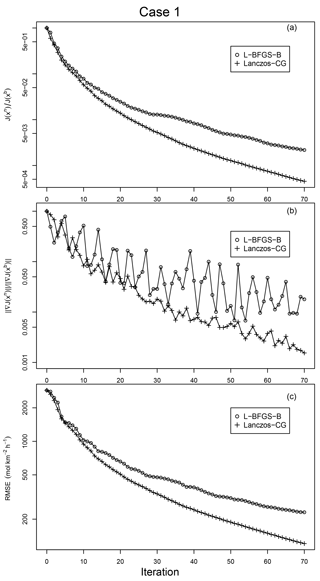
Figure 13Results of the inverse modeling experiment (Case 1). Panel (a) shows the reduction of the cost function, represented by J(xn)∕J(xb). Panel (b) shows the reduction of the gradient norm, represented by . Panel (c) shows the reduction of biospheric CO2 flux RMSE.
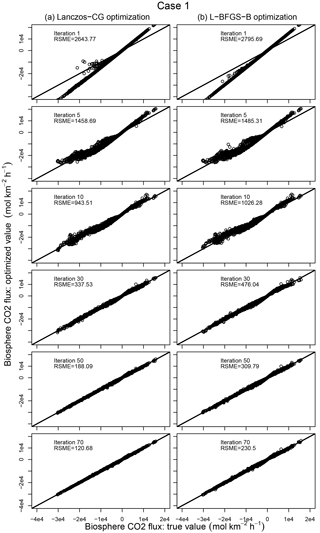
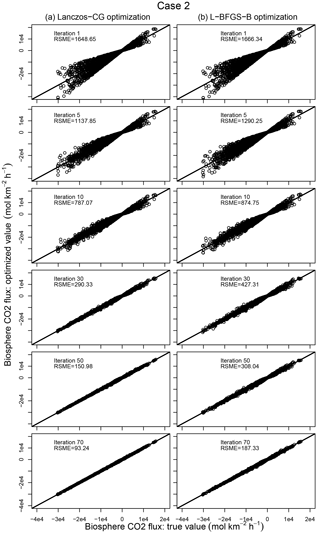
Figure 14Comparison between the true and optimized CO2 fluxes by Lanczos-CG (left column) and L-BFGS-B (right column) in the inverse modeling experiment (Case 1). The comparison and RMSE after the 1st, 5th, 10th, 30th, 50th, and 70th iterations are shown in the figure. All iterations of Lanczos-CG are from one outer loop.
3.4 Inverse modeling tests
3.4.1 Inverse modeling setup
The sensitivity tests in Sect. 3.2 have confirmed that the tangent linear and adjoint models of WRF-CO2 4D-Var are correctly implemented. In this section, inverse modeling tests are conducted to confirm that the two optimization schemes described in Sect. 2.2 and 2.3 are also correctly implemented. The inverse modeling tests here are designed following the approach used in Henze et al. (2007). To confirm that the GEOS-Chem 4D-Var code was correctly developed, Henze et al. (2007) set and R=I (the identity matrix) and constrained the optimizations with error-free pseudo-observations. Because , analysis deviations from the first guess cause no increase in the cost function (see Eq. 3). This means that if the 4D-Var code is correctly implemented, the optimization will converge to the true solution used to generate the pseudo-observations. Such a configuration of B and R, although highly ideal and unrealistic for real applications, is an effective way to test the code accuracy in isolation from external errors. If the code is correctly implemented, the optimization will converge to the true solution used to generate the pseudo-observations. Because the background error is set to infinity (), the optimization should converge to the true solution with any first guess. A different first guess will impact the process of the convergence but not the result: the optimization should eventually converge to the true solution. Following Henze et al. (2007), inverse modeling tests here involve the following steps:
-
Run the WRF-CO2 forward model for 24 h using the daily mean biospheric CO2 flux (Fig. 4) as the true biospheric CO2 fluxes.
-
Generate pseudo-observations by saving the model-simulated atmospheric CO2 at all grid points of the bottom 30 vertical levels every 4 h. This creates a set of six pseudo-observation files, which contain no error with respect to the true biospheric CO2 flux used in Step 1.
-
Generate a set of first-guess biospheric CO2 fluxes.
-
Set the background error to infinity () and the observation error to the identity matrix ().
-
Run the L-BFGS-B and incremental optimizations with the first-guess biospheric CO2 flux (Step 3), constrained by the pseudo-observations (Step 2), until the optimized biospheric flux converges to the true biospheric CO2 flux (Step 1).
Repeat Steps 3–5 twice for two different sets of first-guess biospheric CO2 fluxes:
-
Case 1: set flux scaling factor kco2=1.5 at all surface grid point.
-
Case 2: set flux scaling factor kco2 randomly distributed between 0.5 and 1.5.
Figure 12 shows the two sets of first-guess biospheric CO2 as compared with the true biospheric CO2 fluxes. Each point in the figures represents a surface grid point. It should be noted that because the Case 1 first guess overestimates the true fluxes by 50 % at all surface grid points, the background error is perfectly correlated, implying that all off-diagonal elements in B should be set to unity. However, since the inverse modeling tests are designed to be driven solely by the pseudo-observations (by setting ), the detailed content of B becomes irrelevant. It should also be noted that the same set of pseudo-observations (Step 1) is used for both of the two cases of first guesses, and the pseudo-observations were not perturbed with errors; it is appropriate to set R=I for both cases. This simply assigns all the observations equal weight in calculating the observation cost function using Eq. (4). In these inverse modeling tests, because the pseudo-observations are of qco2 at the forward model's grid points, the mapping between model space and observation space is trivial: the observation operator (H), tangent linear observation operator (), and adjoint observation operator () are all simply the identity matrix. For application with real observations, however, each type of CO2 observations will need its own set of H, , and to map between the model space and observation space.
A very simple error configuration (, and R=I) was used in the inverse modeling tests here, but such a setting is only appropriate to confirm code accuracy using error-free observations. For real data applications, an appropriate specification of background (B) and observation error (R) is a critical and challenging task. Ideally, the variance and covariance in B should be specified based on comparisons between prior fluxes and accurate flux measurements (Chevallier et al., 2006; Gerbig et al., 2006). But available flux measurements are often of insufficient amount, thus necessitating assumptions regarding the form of the background error matrix. For instance, prior flux errors were treated as uncorrelated in Gockede et al. (2010), and Rodenbeck et al. (2003) used an exponential decaying spatial correlation for the prior flux error. In another study, Peylin et al. (2005) found that significantly different flux estimation resulted from varying the prior flux error correlation scale from 500 to 2000 km. For the observation error covariance matrix R, the spatial and temporal error correlations were often neglected in earlier inversion studies (Gurney et al., 2002; Pillai et al., 2016). With more recent inversion studies using continuous observation at towers (Law et al., 2008), airborne observations (Lauvaux et al., 2008), and satellite observations (Chevallier et al., 2005), attempts have been made to represent the spatial and temporal correlations of observation errors. For instance, Kountouris et al. (2015) found the temporal autocorrelation time for observation data using the VPRM model is around 30 days.
3.4.2 Inverse modeling results
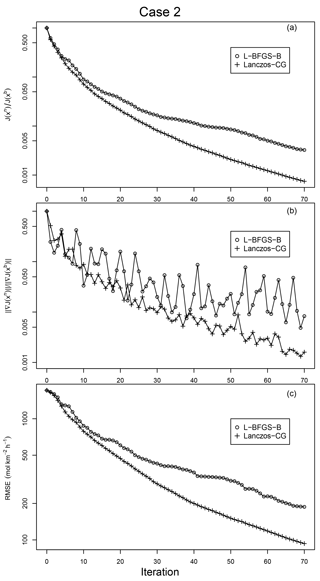
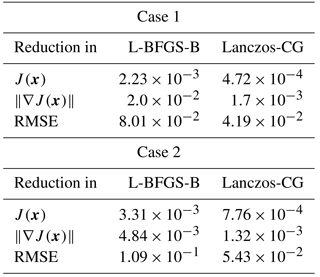
The results from inverse modeling experiments with Case 1 prior are shown in Figs. 13 and 14. Figure 13 shows the iterative reduction of the cost function J(x), gradient norm , and RMSE. The iteration number for Lanczos-CG is all from its inner loop, and only one outer loop is used. The figures show both L-BFGS-B and Lanczos-CG reduce the cost function monotonically. In about the first 10 iterations, the cost function reduction is more or less similar for the two optimization schemes, but Lanczos-CG starts to gradually outperform L-BFGS-B after. In gradient norm reduction, both schemes feature periodic oscillations embedded in the large-scale downward trend. By comparison, Lanczos-CG has a smaller magnitude oscillation and steeper downward trend than L-BFGS-B. It should be noted that while L-BFGS-B calculates cost function and its gradient in each iteration, Lanczos-CG only approximates these values in its inner loop. The cost function and gradient norm from Lanczos-CG shown in Fig. 13 are calculated by extra calls to the forward and adjoint models in each inner iteration, which doubles the computation cost and is not needed in actual inversion applications. Figure 13c shows that both optimization schemes reduce RMSE of daily biosphere flux monotonically, and Lanczos-CG achieves better reduction after about the first 10 iterations. Figure 14 shows the snapshots of the optimized daily mean biosphere flux (obtained as the product of the prior flux and the optimized scaling factor) at a selected set of iterations. These figures depict the iterative process of priors converging to the true solution.
The results of inverse modeling experiments using Case 2 prior are shown in Figs. 15 and 16. The reductions of J(x), , and RMSE are similar to Case 1 in that Lanczos-CG substantially outperforms L-BFGS-G after about the first 10 iterations. Table 5 summarizes the results from all four inverse modeling experiments described above. It must be pointed out that these inverse modeling results are obtained from a highly unphysical setup, and they are not the expected level of performance (in terms of cost function and RMSE reduction) that would be obtained in a inversion with real observations.
The lateral tracer boundary condition is necessary to connect regional tracer simulations to the global background tracer distribution (Gerbig et al., 2003). A number of regional inversion studies have explored the sensitivity of the estimated posterior flux to the lateral boundary condition. For instance, Schuh et al. (2010) found a 30 % magnitude difference in the retrieved North American biospheric flux when boundary conditions from two different global models were used (CarbonTracker and PCTM). In an inversion study over the state of Oregon, Gockede et al. (2010) found the estimated biospheric CO2 fluxes were highly sensitive to systematic changes in the advected background CO2 through the lateral boundaries. To address the lateral boundary uncertainty, Lauvaux et al. (2008) used LPDM backward trajectories to calculate the atmospheric CO2 sensitivity to the lateral boundary conditions, and optimized lateral boundary conditions along with surface fluxes in a synthesis inversion approach. An alternative is to use part of the observations to correct the lateral boundary error before the inversion, which then only includes surface fluxes in its state vector (Lauvaux et al., 2012). In the pseudo-observation-based inverse modeling tests described in Sect. 3 of this work, CO2 lateral boundary conditions do not contain error, and they were not included in the state vector for optimization. When WRF-CO2 4D-Var is applied with real observations, uncertainties of lateral boundary conditions need to be appropriately treated. To use either approach used in Lauvaux et al. (2008) or in Lauvaux et al. (2012), the adjoint code for tracer lateral boundary conditions would need to be developed for the WRF-CO2 4D-Var system.
Table 4Summary of CO2 tower sites. Sensitivity as calculated by WRF-CO2 4D-Var's tangent linear and adjoint models is compared against finite difference sensitivity at these sites.

Table 5Summary of inverse modeling experiment results. The reductions of cost function J(x), gradient norm , and RMSE are given as the ratio to their respective starting values. Results of the two experiment cases are the values after 70 iterations.
In the WRF-Chem dynamical core, chemistry mixing ratios are updated at each time step by the advection and diffusion tendencies. Then, chemistry mixing ratios at the lateral boundaries are updated with the chemistry boundary condition using the flow-dependent method, which uses the horizontal wind direction to determine whether the chemistry mixing ratio at a boundary grid point should be updated by the lateral boundary. If the horizontal wind direction indicates tracer inflow at a boundary grid, Eq. (9) will be applied to the grid point:
where qco2 represents CO2 mixing ratio at a lateral boundary grid, qb and qb,t are the CO2 mixing ratio and tendency at the corresponding lateral boundary. To develop the lateral-boundary-related tangent linear and adjoint code, Eq. (9) is replaced by Eq. (10) in WRF-CO2 4D-Var:
where kco2 represents the CO2 lateral boundary scaling factor. Please note that in Eqs. (9) and (10), the time dependence has been dropped for the sake of simplicity. The corresponding tangent linear and adjoint variables of Eq. (10) are given in Eqs. (11) and (12):
where g_qco2 and a_qco2 are the tangent linear and adjoint variables of qco2, and g_kco2 and a_kco2 are the tangent linear and adjoint variables of kco2.
Most code development for tracer lateral boundary conditions is in the input_chem_data module of the chemistry directory, along with some additional code modification to enable the lateral boundary condition variables to be passed forward (kco2 and g_kco2) and backward (a_kco2) in time. The two optimization schemes of WRF-CO2 4D-Var have also been implemented to allow for flexibilities in state vector specification. The user can choose to include lateral boundary conditions in the state vector to be optimized, which is a similar approach to that in Lauvaux et al. (2008) (but using a 4D-Var optimization). Alternatively, the user can choose to correct the lateral boundary (using the adjoint model) before the inversion and not to include lateral boundary in the state vector (Lauvaux et al., 2012).
When applied with real observations, whether and how to aggregate lateral boundary scaling factors is not trivial (Lauvaux et al., 2008, 2012). On the one hand, including lateral boundary scaling factors without spatial aggregation will greatly increase the state vector size, likely causing the inversion to be underconstrained. On the other hand, aggregating lateral boundary scaling factors may cause aggregation error (Kaminski et al., 2001). While the actual treatment of lateral boundary scaling factor aggregation is beyond the scope of this work, a mapping mechanism has been implemented in WRF-CO2 4D-Var to facilitate the aggregation. In WRF-CO2 4D-Var, qco2, g_qco2, and a_qco2 are defined on the model grid, but kco2, g_kco2, and a_kco2 are defined as 1-D variables in the state vector. The mapping mechanism implemented in procedure da_cv_to_wrf and its adjoint counterpart allows for many-to-one mappings from the 3-D grid variables to the 1-D state vector. This mapping mechanism allows the user flexibility in determining whether and how to aggregate the lateral boundary condition.
WRF-CO2 4D-Var was developed as a data assimilation system designed to constrain surface CO2 fluxes by combining an online atmospheric chemistry transport model and observation data in a Bayesian framework. Two optimization schemes were implemented for cost function minimization. The first is based on L-BFGS-B, and the second is an incremental optimization using Lanczos-CG. The cost function and its gradient required by the optimization schemes are calculated by WRF-CO2 4D-Var's three component models: forward, tangent linear, and adjoint models, all developed on top of the WRFPLUS system. While WRFPLUS's forward model is WRF, WRF-Chem was used as WRF-CO2 4D-Var's forward model to include CO2 in the system, and the tangent linear and adjoint models were modified to keep their consistency with the forward model. Like most other CO2 inverse modeling systems, WRF 4D-Var ignores the possible impacts of atmospheric CO2 variation on the meteorology. This simplification enables the use of the same full physical parameterizations in the forward, tangent linear, and adjoint models. This configuration reduces linearization error while allowing the WRF system's large number of physical parameterizations to be used in WRF-CO2 4D-Var without requiring a large amount of new code development.
WRF-CO2 4D-Var's tangent linear and adjoint models were tested by comparing their sensitivities' spatial patterns with the dominant wind patterns. The results make physical sense given the meteorological transport. The accuracy of tangent linear and adjoint models was evaluated by comparing their sensitivity against finite difference sensitivity calculated by the forward model. The results show that both tangent linear and adjoint sensitivities agree well with finite difference sensitivity. Finally, the system was tested in inverse modeling with pseudo-observations, and the results show that both optimization schemes successfully recovered the true values with reasonable accuracy and computation cost.
While Lanczos-CG performs better than L-BFGS-B in the inverse modeling tests, it must be pointed out that the tests are very limited. Although a comprehensive comparison between the two optimization schemes is beyond the scope of the present paper, it is important to point out some of their differences as implemented in WRF-CO2 4D-Var. First, the Lanczos-CG calls the tangent linear model in each inner loop iteration, while L-BFGS-B calls the forward model. For a tracer transport system like WRF-CO2 4D-Var, the tangent linear model can skip some of the costly physics parameterizations, such as the radiation scheme. This difference means that typically the tangent linear model is faster than the forward model, and as a result Lanczos-CG runs faster than L-BFGS-B. In our inversion modeling experiments (24 h simulation with Δt=120 s, 30-processor core), it takes about 10 min wall time to complete one inner loop of Lanczos-CG. L-BFGS-B takes about 10 % more wall time to complete one iteration.
Second, provided with the cost function and its gradient, each iteration of L-BFGS-B calculates an updated state vector from its previous iteration. In WRF-CO2 4D-Var, this calculation is carried out on only the root core and broadcasted to the other process cores. In comparison, Lanczos-CG calculates the state vector increment based on the cost function gradient alone (without the need for J(x)). The calculation is carried out on each processor core. The above difference has implications for memory requirements. The main memory allocation for L-BFGS-B is its workspace array, which is about , where n is the size of the state vector (x), and k is the number of corrections used in the limited memory matrix. This memory allocation is only needed on the root core. The value of k is set by the user, and the recommended value is between 3 and 20. In comparison, Lanczos-CG requires a memory size of about m×n on each processor core, where m is the maximal inner loop iteration allowed. Although it is possible to reduce the per processor core a memory allocation from m×n to n by deactivating the modified Gram–Schmidt orthonormalization step, it is typically not recommended.
Another consideration for memory requirements is related to I/O time cost. WRFPLUS saves its entire trajectory in memory to avoid expensive I/O operations. This is not a practical solution for WRF-CO2 4D-Var, which is designed to run a longer simulation than the typical 6 h run intended for WRFDA. GH15/17 implemented a second-order checkpoint mechanism to overcome the memory limit. This approach breaks the whole simulation period into sections and saves restart files at the end of each section by the forward model. This approach requires extra calls of the forward model to recalculate the trajectory for each section during backward integration (see Fig. 3 of GH15). In WRF-CO2 4D-Var, a different approach was implemented to overcome this memory limit: the forward model saves the trajectory at each time step in memory, as WRFPLUS does. After a number of integration steps, the memory on each task processor core is dumped to an external file, and the memory is then reused. Each external file is marked with its starting time stamp and the processor core it belongs to. For instance, a 24 h simulation with 120 s time step will have a total of 720 steps. If the system saves its trajectory to external files each 30 time steps, memory allocation on each task processor core is only needed for 30 steps instead of 720 steps. This will result in 24 (720/30) trajectory files on each task processor core, and the total number of trajectory files depends on the number of processor cores used. These trajectory files are read by both tangent linear and adjoint models in a similar way to standard WRF auxiliary files. In the above example, they are read in at each 30 time steps, substantially reducing I/O time compared with reading in at each step. These trajectory files are different from standard WRF auxiliary files in that each file belongs to an individual processor core, rather than being shared among all processor cores. This means all model runs in an inverse experiment must use the same domain patch configuration, which is the most common practice.
In future development, we plan to implement observation operators for real observations, including those from towers, satellites, and airborne instruments. This is required for applying WRF-CO2 4D-Var with real observations. As a regional inverse system, the correct treatment of tracer lateral boundary conditions is important. We plan to test the lateral boundary condition adjoint code (Sect. 4) in a follow-up study. In addition, future applications of WRF-CO2 4D-Var with real observations must use proper treatment of observation and background error covariance, which was not tackled in the pseudo-observation tests in the present paper.
In addition, we also plan to periodically update the WRF-CO2 4D-Var system to keep up with WRF system updates. Such updates will mainly consist of replacing the forward model with the updated WRF code and developing the tangent linear and adjoint code for the relevant updated procedures. As the variable dependence analysis (Sect. 2.4.1) indicates that the tangent linear and adjoint code is only needed for a portion of WRF procedures, the amount of work required for updating WRF-CO2 4D-Var is manageable. In addition, future development of WRF-CO2 4D-Var will also be dependent on updates to WRFPLUS, which has always been updated along with WRF.
WRF-CO2 4D-Var source code can be retrieved via https://doi.org/10.5281/zenodo.1220407 (Zheng et al., 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-1725-2018-supplement.
The authors declare that they have no conflict of interest.
The authors express their appreciation for the WRF/WRF-Chem/WRFDA/WRFPLUS
development teams for making their code available in the public domain.
Discussion with Joel LeBlanc of Michigan Tech Research Institute
(MTRI) improved the optimization schemes' implementation and presentation in
this paper. The insightful and detailed comments from the three reviewers
greatly improved both the model and the paper. This work was partially
supported by a Central Michigan University CST research incentive fund. This
is contribution 98 of the Central Michigan University Institute for Great
Lakes Research.
Edited by: Tomomichi Kato
Reviewed by: three anonymous referees
Alden, C. B., Miller, J. B., Gatti, L. V., Gloor, M. M., Guan, K., Michalak, A. M., van der Laan-Luijkx, I. T., Touma, D., Andrews, A., Basso, L. S., Correia, C. S. C., Domingues, L. G., Joiner, J., Krol, M. C., Lyapustin, A. I., Peters, W., Shiga, Y. P., Thoning, K., van der Velde, I. R., van Leeuwen, T. T., Yadav, V., and Diffenbaugh, N. S.: Regional atmospheric CO2 inversion reveals seasonal and geographic differences in Amazon net biome exchange, Global Change Biol., 22, 3427–3443, 2016. a, b
Appel, K. W., Napelenok, S. L., Foley, K. M., Pye, H. O. T., Hogrefe, C., Luecken, D. J., Bash, J. O., Roselle, S. J., Pleim, J. E., Foroutan, H., Hutzell, W. T., Pouliot, G. A., Sarwar, G., Fahey, K. M., Gantt, B., Gilliam, R. C., Heath, N. K., Kang, D., Mathur, R., Schwede, D. B., Spero, T. L., Wong, D. C., and Young, J. O.: Description and evaluation of the Community Multiscale Air Quality (CMAQ) modeling system version 5.1, Geosci. Model Dev., 10, 1703–1732, https://doi.org/10.5194/gmd-10-1703-2017, 2017. a
Baker, D. F., Doney, S. C., and Schimel, D. S.: Variational data assimilation for atmospheric CO2, Tellus B, 58, 359–365, 2006. a
Baker, D. F., Bösch, H., Doney, S. C., O'Brien, D., and Schimel, D. S.: Carbon source/sink information provided by column CO2 measurements from the Orbiting Carbon Observatory, Atmos. Chem. Phys., 10, 4145–4165, https://doi.org/10.5194/acp-10-4145-2010, 2010. a, b
Barker, D., Huang, X.-Y., Liu, Z., Auligne, T., Zhang, X., Rugg, S., Ajjaji, R., Bourgeois, A., Bray, J., Chen, Y., Demirtas, M., Guo, Y.-R., Henderson, T., Huang, W., Lin, H.-C., Michalakes, J., Rizvi, S., and Zhang, X.: The Weather Research and Forecasting Model's Community Variational/Ensemble Data Assimilation System WRFDA, B. Am. Meteorol. Soc., 93, 831–843, 2012. a, b, c, d
Basu, S., Houweling, S., Peters, W., Sweeney, C., Machida, T., Maksyutov, S., Patra, P. K., Saito, R., Chevallier, F., Niwa, Y., Matsueda, H., and Sawa, Y.: The seasonal cycle amplitude of total column CO2: Factors behind the model-observation mismatch, J. Geophys. Res, 116, d23306, https://doi.org/10.1029/2011JD016124, 2011. a
Basu, S., Guerlet, S., Butz, A., Houweling, S., Hasekamp, O., Aben, I., Krummel, P., Steele, P., Langenfelds, R., Torn, M., Biraud, S., Stephens, B., Andrews, A., and Worthy, D.: Global CO2 fluxes estimated from GOSAT retrievals of total column CO2, Atmos. Chem. Phys., 13, 8695–8717, https://doi.org/10.5194/acp-13-8695-2013, 2013. a
Bocquet, M.: Toward Optimal Choices of Control Space Representation for Geophysical Data Assimilation, Mon. Weather Rev., 137, 2331–2348, 2009. a
Bocquet, M., Elbern, H., Eskes, H., Hirtl, M., Žabkar, R., Carmichael, G. R., Flemming, J., Inness, A., Pagowski, M., Pérez Camaño, J. L., Saide, P. E., San Jose, R., Sofiev, M., Vira, J., Baklanov, A., Carnevale, C., Grell, G., and Seigneur, C.: Data assimilation in atmospheric chemistry models: current status and future prospects for coupled chemistry meteorology models, Atmos. Chem. Phys., 15, 5325–5358, https://doi.org/10.5194/acp-15-5325-2015, 2015. a
Bousquet, P., Ciais, P., Peylin, P., Ramonet, M., and Monfray, P.: Inverse modeling of annual atmospheric CO2 sources and sinks 1. Method and control inversion, J. Geophys. Res, 104, 26161–26178, 1999. a
Bruhwiler, L. M. P., Michalak, A. M., Peters, W., Baker, D. F., and Tans, P.: An improved Kalman Smoother for atmospheric inversions, Atmos. Chem. Phys., 5, 2691–2702, https://doi.org/10.5194/acp-5-2691-2005, 2005. a, b
Butler, M. P., Davis, K. J., Denning, A. S., and Kawa, S. R.: Using continental observations in global atmospheric inversions of CO2: North American carbon sources and sinks, Tellus B, 62, 550–572, 2010. a
Byrd, R. H., Lu, P., and Nocedal, J.: A limited memory algorithm for bound constrained optimization, SIAM J. Sci. Stat. Comp., 16, 1190–1208, 1995. a, b
Chan, E., Chan, D., Ishizawa, M., Vogel, F., Brioude, J., Delcloo, A., Wu, Y., and Jin, B.: Description and evaluation of REFIST v1.0: a regional greenhouse gas flux inversion system in Canada, Geosci. Model Dev. Discuss., https://doi.org/10.5194/gmd-2016-213, 2016. a
Chevallier, F.: Impact of correlated observation errors on inverted CO2 surface fluxes from OCO measurements, Geophys. Res. Lett., 34, https://doi.org/10.1029/2007GL030463, 2007. a
Chevallier, F., Fisher, M., Peylin, P., Serrar, S., Bousquet, P., Breon, F. M., Chedin, A., and Ciais, P.: Inferring CO2 sources and sinks from satellite observations: Method and application to TOVS data, J. Geophys. Res., 110, d24309, https://doi.org/10.1029/2005JD006390, 2005. a, b, c
Chevallier, F., Ciais, P., Conway, T. J., Aalto, T., Anderson, B. E., Bousquet, P., Brunke, E. G., Ciattaglia, L., Esaki, Y., Froehlich, M., Gomez, A., Gomez-Pelaez, A. J., Haszpra, L., Krummel, P. B., Langenfelds, R. L., Leuenberger, M., Machida, T., Maignan, F., Matsueda, H., Morgui, J. A., Mukai, H., Nakazawa, T., Peylin, P., Ramonet, M., Rivier, L., Sawa, Y., Schmidt, M., Steele, L. P., Vay, S. A., Vermeulen, A. T., Wofsy, S., and Worthy, D.: CO2 surface fluxes at grid point scale estimated from a global 21 year reanalysis of atmospheric measurements, J. Geophys. Res., 115, d21307, https://doi.org/10.1029/2010JD013887, 2010. a
Chevallier, F., Viovy, N., Reichstein, M., and Ciais, P.: On the assignment of prior errors in Bayesian inversions of CO2 surface fluxes, Geophys. Res. Lett., 33, https://doi.org/10.1029/2006GL026496, 2006. a
Chou, M. D. and Suarez, M.: A solar radiation parameterization for atmospheric studies, Tech. Rep. NASA/TM-1999-10460, Vol. 15, 38 pp., NASA, 1999. a
Ciais, P., Dolman, A. J., Bombelli, A., Duren, R., Peregon, A., Rayner, P. J., Miller, C., Gobron, N., Kinderman, G., Marland, G., Gruber, N., Chevallier, F., Andres, R. J., Balsamo, G., Bopp, L., Bréon, F.-M., Broquet, G., Dargaville, R., Battin, T. J., Borges, A., Bovensmann, H., Buchwitz, M., Butler, J., Canadell, J. G., Cook, R. B., DeFries, R., Engelen, R., Gurney, K. R., Heinze, C., Heimann, M., Held, A., Henry, M., Law, B., Luyssaert, S., Miller, J., Moriyama, T., Moulin, C., Myneni, R. B., Nussli, C., Obersteiner, M., Ojima, D., Pan, Y., Paris, J.-D., Piao, S. L., Poulter, B., Plummer, S., Quegan, S., Raymond, P., Reichstein, M., Rivier, L., Sabine, C., Schimel, D., Tarasova, O., Valentini, R., Wang, R., van der Werf, G., Wickland, D., Williams, M., and Zehner, C.: Current systematic carbon-cycle observations and the need for implementing a policy-relevant carbon observing system, Biogeosciences, 11, 3547–3602, https://doi.org/10.5194/bg-11-3547-2014, 2014. a
Deng, F., Jones, D. B. A., Henze, D. K., Bousserez, N., Bowman, K. W., Fisher, J. B., Nassar, R., O'Dell, C., Wunch, D., Wennberg, P. O., Kort, E. A., Wofsy, S. C., Blumenstock, T., Deutscher, N. M., Griffith, D. W. T., Hase, F., Heikkinen, P., Sherlock, V., Strong, K., Sussmann, R., and Warneke, T.: Inferring regional sources and sinks of atmospheric CO2 from GOSAT XCO2 data, Atmos. Chem. Phys., 14, 3703–3727, https://doi.org/10.5194/acp-14-3703-2014, 2014. a
Enting, I. G., Trudinger, C. M., and Francey, R. J.: A Synthesis Inversion of the Concentration and Delta-C-13 of Atmospheric CO2, Tellus B, 47, 35–52, 1995. a
Fowler, A. M. and Lawless, A. S.: An Idealized Study of Coupled Atmosphere–Ocean 4D-Var in the presence of model error, Mon. Weather Rev., 144, 4007–4029, 2016. a, b
Freitas, S. R., Longo, K. M., Alonso, M. F., Pirre, M., Marecal, V., Grell, G., Stockler, R., Mello, R. F., and Sánchez Gácita, M.: PREP-CHEM-SRC – 1.0: a preprocessor of trace gas and aerosol emission fields for regional and global atmospheric chemistry models, Geosci. Model Dev., 4, 419–433, https://doi.org/10.5194/gmd-4-419-2011, 2011. a
French, N. H. F., de Groot, W. J., Jenkins, L. K., Rogers, B. M., Alvarado, E., Amiro, B., de Jong, B., Goetz, S., Hoy, E., Hyer, E., Keane, R., Law, B. E., McKenzie, D., McNulty, S. G., Ottmar, R., Perez-Salicrup, D. R., Randerson, J., Robertson, K. M., and Turetsky, M.: Model comparisons for estimating carbon emissions from North American wildland fire, J. Geophys. Res., 116, https://doi.org/10.1029/2010JG001469, 2011. a
Gerbig, C., Lin, J. C., Wofsy, S. C., Daube, B. C., Andrews, A. E., Stephens, B. B., Bakwin, P. S., and Grainger, C. A.: Toward constraining regional-scale fluxes of CO2 with atmospheric observations over a continent: 1. Observed spatial variability from airborne platforms, J. Geophys. Res, 108, 4756, https://doi.org/10.1029/2002JD003018, 2003. a, b
Gerbig, C., Lin, J. C., Munger, J. W., and Wofsy, S. C.: What can tracer observations in the continental boundary layer tell us about surface-atmosphere fluxes?, Atmos. Chem. Phys., 6, 539–554, https://doi.org/10.5194/acp-6-539-2006, 2006. a
Gerbig, C., Körner, S., and Lin, J. C.: Vertical mixing in atmospheric tracer transport models: error characterization and propagation, Atmos. Chem. Phys., 8, 591–602, https://doi.org/10.5194/acp-8-591-2008, 2008. a, b, c
Gerbig, C., Dolman, A. J., and Heimann, M.: On observational and modelling strategies targeted at regional carbon exchange over continents, Biogeosciences, 6, 1949–1959, https://doi.org/10.5194/bg-6-1949-2009, 2009. a, b
Gockede, M., Turner, D. P., Michalak, A. M., Vickers, D., and Law, B. E.: Sensitivity of a subregional scale atmospheric inverse CO2 modeling framework to boundary conditions, J. Geophys. Res., 115, https://doi.org/10.1029/2010JD014443, 2010. a, b
Gourdji, S. M., Mueller, K. L., Yadav, V., Huntzinger, D. N., Andrews, A. E., Trudeau, M., Petron, G., Nehrkorn, T., Eluszkiewicz, J., Henderson, J., Wen, D., Lin, J., Fischer, M., Sweeney, C., and Michalak, A. M.: North American CO2 exchange: inter-comparison of modeled estimates with results from a fine-scale atmospheric inversion, Biogeosciences, 9, 457–475, https://doi.org/10.5194/bg-9-457-2012, 2012. a, b
Grell, G. and Devenyi, D.: A generalized approach to parameterizing convection combining ensemble and data assimilation techniques, Geophys. Res. Lett., 29, https://doi.org/10.1029/2002GL015311, 2002. a
Grell, G. A. and Freitas, S. R.: A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling, Atmos. Chem. Phys., 14, 5233–5250, https://doi.org/10.5194/acp-14-5233-2014, 2014. a, b, c
Grell, G. A., Knoche, R., Peckham, S. E., and McKeen, S. A.: Online versus offline air quality modeling on cloud-resolving scales, Geophys. Res. Lett., 31, L16117, https://doi.org/10.1029/2004GL020175 2004. a, b
Grell, G. A., Peckham, S. E., Schmitz, R., McKeen, S. A., Frost, G., Skamarock, W. C., and Eder, B.: Fully coupled online chemistry within the WRF model, Atmos. Environ., 39, 6957–6975, 2005. a
Guerrette, J. J. and Henze, D. K.: Development and application of the WRFPLUS-Chem online chemistry adjoint and WRFDA-Chem assimilation system, Geosci. Model Dev., 8, 1857–1876, https://doi.org/10.5194/gmd-8-1857-2015, 2015. a
Guerrette, J. J. and Henze, D. K.: Four-dimensional variational inversion of black carbon emissions during ARCTAS-CARB with WRFDA-Chem, Atmos. Chem. Phys., 17, 7605–7633, https://doi.org/10.5194/acp-17-7605-2017, 2017. a
Gupta, S., McNider, R., Trainer, M., Zamora, R., Knupp, K., and Singh, M.: Nocturnal wind structure and plume growth rates due to inertial oscillations, J. Appl. Meteorol. Climatol., 36, 1050–1063, 1997. a
Gurney, K. R., Law, R. M., Denning, A. S., Rayner, P. J., Baker, D., Bousquet, P., Bruhwiler, L., Chen, Y. H., Ciais, P., Fan, S., Fung, I. Y., Gloor, M., Heimann, M., Higuchi, K., John, J., Maki, T., Maksyutov, S., Masarie, K., Peylin, P., Prather, M., Pak, B. C., Randerson, J., Sarmiento, J., Taguchi, S., Takahashi, T., and Yuen, C. W.: Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models, Nature, 415, 626–630, 2002. a, b, c
Gurney, K. R., Chen, Y. H., Maki, T., Kawa, S. R., Andrews, A., and Zhu, Z. X.: Sensitivity of atmospheric CO2 inversions to seasonal and interannual variations in fossil fuel emissions, J. Geophys. Res., 110, d10308, https://doi.org/10.1029/2004JD005373, 2005. a
Hascoet, L. and Pascual, V.: The Tapenade Automatic Differentiation Tool: Principles, Model, and Specification, ACM Trans. Math. Software, 39, 20, https://doi.org/10.1145/2450153.2450158, 2013. a
Henze, D. K., Hakami, A., and Seinfeld, J. H.: Development of the adjoint of GEOS-Chem, Atmos. Chem. Phys., 7, 2413–2433, https://doi.org/10.5194/acp-7-2413-2007, 2007. a, b, c, d, e
Hourdin, F., Musat, I., Bony, S., Braconnot, P., Codron, F., Dufresne, J. L., Fairhead, L., Filiberti, M. A., Friedlingstein, P., Grandpeix, J. Y., Krinner, G., Levan, P., Li, Z. X., and Lott, F.: The LMDZ4 general circulation model: climate performance and sensitivity to parametrized physics with emphasis on tropical convection, Climate Dyn., 27, 787–813, 2006. a, b
Houweling, S., Aben, I., Breon, F.-M., Chevallier, F., Deutscher, N., Engelen, R., Gerbig, C., Griffith, D., Hungershoefer, K., Macatangay, R., Marshall, J., Notholt, J., Peters, W., and Serrar, S.: The importance of transport model uncertainties for the estimation of CO2 sources and sinks using satellite measurements, Atmos. Chem. Phys., 10, 9981–9992, https://doi.org/10.5194/acp-10-9981-2010, 2010. a
Hu, X.-M., Nielsen-Gammon, J. W., and Zhang, F.: Evaluation of Three Planetary Boundary Layer Schemes in the WRF Model, J. Appl. Meteorol. Climatol., 49, 1831–1844, 2010. a
Huang, X.-Y., Xiao, Q., Barker, D. M., Zhang, X., Michalakes, J., Huang, W., Henderson, T., Bray, J., Chen, Y., Ma, Z., Dudhia, J., Guo, Y., Zhang, X., Won, D.-J., Lin, H.-C., and Kuo, Y.-H.: Four-Dimensional Variational Data Assimilation for WRF: Formulation and Preliminary Results, Mon. Weather Rev., 137, 299–314, 2009. a, b
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res., D13103, https://doi.org/10.1029/2008JD009944, 113, 2008. a
Jiang, X., Li, Q. B., Liang, M. C., Shia, R. L., Chahine, M. T., Olsen, E. T., Chen, L. L., and Yung, Y. L.: Simulation of upper tropospheric CO2 from chemistry and transport models, Global Biogeochem. Cy., 22, gB4025, https://doi.org/10.1029/2007GB003049, 2008. a
Kaminski, T., Rayner, P. J., Heimann, M., and Enting, I. G.: On aggregation errors in atmospheric transport inversions, J. Geophys. Res., 106, 4703–4715, 2001. a, b
Kawa, S. R., Erickson, D. J., Pawson, S., and Zhu, Z.: Global CO2 transport simulations using meteorological data from the NASA data assimilation system, J. Geophys. Res., 109, d18312, https://doi.org/10.1029/2004JD004554, 2004. a
Kopacz, M., Jacob, D. J., Henze, D. K., Heald, C. L., Streets, D. G., and Zhang, Q.: Comparison of adjoint and analytical Bayesian inversion methods for constraining Asian sources of carbon monoxide using satellite (MOPITT) measurements of CO columns, J. Geophys. Res., 114, d04305, https://doi.org/10.1029/2007JD009264, 2009. a
Kountouris, P., Gerbig, C., Totsche, K.-U., Dolman, A. J., Meesters, A. G. C. A., Broquet, G., Maignan, F., Gioli, B., Montagnani, L., and Helfter, C.: An objective prior error quantification for regional atmospheric inverse applications, Biogeosciences, 12, 7403–7421, https://doi.org/10.5194/bg-12-7403-2015, 2015. a
Krol, M., Houweling, S., Bregman, B., van den Broek, M., Segers, A., van Velthoven, P., Peters, W., Dentener, F., and Bergamaschi, P.: The two-way nested global chemistry-transport zoom model TM5: algorithm and applications, Atmos. Chem. Phys., 5, 417–432, https://doi.org/10.5194/acp-5-417-2005, 2005. a
Lanczos, C.: An Iteration Method for the Solution of the Eigenvalue Problem of Linear Differential and Integral Operators, J. Res. Nat. Bur. Stand., 45, 255–282, 1950. a, b
Lauvaux, T., Schuh, A. E., Uliasz, M., Richardson, S., Miles, N., Andrews, A. E., Sweeney, C., Diaz, L. I., Martins, D., Shepson, P. B., and Davis, K. J.: Constraining the CO2 budget of the corn belt: exploring uncertainties from the assumptions in a mesoscale inverse system, Atmos. Chem. Phys., 12, 337–354, https://doi.org/10.5194/acp-12-337-2012, 2012. a, b, c, d, e
Lauvaux, T., Uliasz, M., Sarrat, C., Chevallier, F., Bousquet, P., Lac, C., Davis, K. J., Ciais, P., Denning, A. S., and Rayner, P. J.: Mesoscale inversion: first results from the CERES campaign with synthetic data, Atmos. Chem. Phys., 8, 3459–3471, https://doi.org/10.5194/acp-8-3459-2008, 2008. a, b, c, d, e
Law, R. M., Peters, W., Roedenbeck, C., Aulagnier, C., Baker, I., Bergmann, D. J., Bousquet, P., Brandt, J., Bruhwiler, L., Cameron-Smith, P. J., Christensen, J. H., Delage, F., Denning, A. S., Fan, S., Geels, C., Houweling, S., Imasu, R., Karstens, U., Kawa, S. R., Kleist, J., Krol, M. C., Lin, S. J., Lokupitiya, R., Maki, T., Maksyutov, S., Niwa, Y., Onishi, R., Parazoo, N., Patra, P. K., Pieterse, G., Rivier, L., Satoh, M., Serrar, S., Taguchi, S., Takigawa, M., Vautard, R., Vermeulen, A. T., and Zhu, Z.: TransCom model simulations of hourly atmospheric CO2: Experimental overview and diurnal cycle results for 2002, Global Biogeochem. Cy., 22, gB3009, https://doi.org/10.1029/2007GB003050, 2008. a
Lin, J. C., Gerbig, C., Wofsy, S. C., Andrews, A. E., Daube, B. C., Davis, K. J., and Grainger, C. A.: A near-field tool for simulating the upstream influence of atmospheric observations: The Stochastic Time-Inverted Lagrangian Transport (STILT) model, J. Geophys. Res., 108, 4493, https://doi.org/10.1029/2002JD003161, 2003. a, b
Liu, J., Bowman, K. W., Lee, M., Henze, D. K., Bousserez, N., Brix, H., Collatz, G. J., Menemenlis, D., Ott, L., Pawson, S., Jones, D., and Nassar, R.: Carbon monitoring system flux estimation and attribution: impact of ACOS-GOSAT X-CO2 sampling on the inference of terrestrial biospheric sources and sinks, Tellus B, 66, 22486, https://doi.org/10.3402/tellusb.v66.22486, 2014. a
Luis Morales, J. and Nocedal, J.: Remark on “Algorithm 778: L-BFGS-B: Fortran Subroutines for Large-Scale Bound Constrained Optimization”, ACM Trans. Math. Software, 38, 7:1–7:4, 2011. a
Mahadevan, P., Wofsy, S. C., Matross, D. M., Xiao, X. M., Dunn, A. L., Lin, J. C., Gerbig, C., Munger, J. W., Chow, V. Y., and Gottlieb, E. W.: A satellite-based biosphere parameterization for net ecosystem CO2 exchange: Vegetation Photosynthesis and Respiration Model (VPRM), Global Biogeochem. Cy., 22, gB2005, https://doi.org/10.1029/2006GB002735, 2008. a
Meirink, J. F., Bergamaschi, P., Frankenberg, C., d'Amelio, M. T. S., Dlugokencky, E. J., Gatti, L. V., Houweling, S., Miller, J. B., Roeckmann, T., Villani, M. G., and Krol, M. C.: Four-dimensional variational data assimilation for inverse modeling of atmospheric methane emissions: Analysis of SCIAMACHY observations, J. Geophys. Res., 113, d17301, https://doi.org/10.1029/2007JD009740, 2008. a, b, c
Michalak, A. M., Bruhwiler, L., and Tans, P. P.: A geostatistical approach to surface flux estimation of atmospheric trace gases, J. Geophys. Res., 109, d14109, https://doi.org/10.1029/2003JD004422, 2004. a
Mlawer, E., Taubman, S., Brown, P., Iacono, M., and Clough, S.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res., 102, 16663–16682, 1997. a
Nassar, R., Jones, D. B. A., Suntharalingam, P., Chen, J. M., Andres, R. J., Wecht, K. J., Yantosca, R. M., Kulawik, S. S., Bowman, K. W., Worden, J. R., Machida, T., and Matsueda, H.: Modeling global atmospheric CO2 with improved emission inventories and CO2 production from the oxidation of other carbon species, Geosci. Model Dev., 3, 689–716, https://doi.org/10.5194/gmd-3-689-2010, 2010 a
Nassar, R., Jones, D. B. A., Kulawik, S. S., Worden, J. R., Bowman, K. W., Andres, R. J., Suntharalingam, P., Chen, J. M., Brenninkmeijer, C. A. M., Schuck, T. J., Conway, T. J., and Worthy, D. E.: Inverse modeling of CO2 sources and sinks using satellite observations of CO2 from TES and surface flask measurements, Atmos. Chem. Phys., 11, 6029–6047, https://doi.org/10.5194/acp-11-6029-2011, 2011. a
Nehrkorn, T., Eluszkiewicz, J., Wofsy, S. C., Lin, J. C., Gerbig, C., Longo, M., and Freitas, S.: Coupled weather research and forecasting-stochastic time-inverted lagrangian transport (WRF-STILT) model, Meteorol. Atmos. Phys., 107, 51–64, 2010. a
Nolte, C. G., Appel, K. W., Kelly, J. T., Bhave, P. V., Fahey, K. M., Collett Jr., J. L., Zhang, L., and Young, J. O.: Evaluation of the Community Multiscale Air Quality (CMAQ) model v5.0 against size-resolved measurements of inorganic particle composition across sites in North America, Geosci. Model Dev., 8, 2877–2892, https://doi.org/10.5194/gmd-8-2877-2015, 2015. a
Peters, W., Jacobson, A. R., Sweeney, C., Andrews, A. E., Conway, T. J., Masarie, K., Miller, J. B., Bruhwiler, L. M. P., Petron, G., Hirsch, A. I., Worthy, D. E. J., van der Werf, G. R., Randerson, J. T., Wennberg, P. O., Krol, M. C., and Tans, P. P.: An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker, P. Natl. Acad. Sci. USA, 104, 18925–18930, 2007. a, b
Peters, W., Miller, J., Whitaker, J., Denning, A., Hirsch, A., Krol, M., Zupanski, D., Bruhwiler, L., and Tans, P.: An ensemble data assimilation system to estimate CO2 surface fluxes from atmospheric trace gas observations, J. Geophys. Res., 110, D34304, https://doi.org/10.1029/2005JD006157, 2005. a, b
Peylin, P., Baker, D., Sarmiento, J., Ciais, P., and Bousquet, P.: Influence of transport uncertainty on annual mean and seasonal inversions of atmospheric CO2 data, J. Geophys. Res., 107, 4385, https://doi.org/10.1029/2001JD000857, 2002. a
Peylin, P., Rayner, P. J., Bousquet, P., Carouge, C., Hourdin, F., Heinrich, P., Ciais, P., and AEROCARB contributors: Daily CO2 flux estimates over Europe from continuous atmospheric measurements: 1, inverse methodology, Atmos. Chem. Phys., 5, 3173–3186, https://doi.org/10.5194/acp-5-3173-2005, 2005. a
Peylin, P., Law, R. M., Gurney, K. R., Chevallier, F., Jacobson, A. R., Maki, T., Niwa, Y., Patra, P. K., Peters, W., Rayner, P. J., Rödenbeck, C., van der Laan-Luijkx, I. T., and Zhang, X.: Global atmospheric carbon budget: results from an ensemble of atmospheric CO2 inversions, Biogeosciences, 10, 6699–6720, https://doi.org/10.5194/bg-10-6699-2013, 2013. a
Pillai, D., Gerbig, C., Kretschmer, R., Beck, V., Karstens, U., Neininger, B., and Heimann, M.: Comparing Lagrangian and Eulerian models for CO2 transport – a step towards Bayesian inverse modeling using WRF/STILT-VPRM, Atmos. Chem. Phys., 12, 8979–8991, https://doi.org/10.5194/acp-12-8979-2012, 2012. a
Pillai, D., Buchwitz, M., Gerbig, C., Koch, T., Reuter, M., Bovensmann, H., Marshall, J., and Burrows, J. P.: Tracking city CO2 emissions from space using a high-resolution inverse modelling approach: a case study for Berlin, Germany, Atmos. Chem. Phys., 16, 9591–9610, https://doi.org/10.5194/acp-16-9591-2016, 2016. a
Pleim, J. and Chang, J.: A nonlocal closure model for vertical mixing in the convective boundary layer, Atmos. Environ., 26, 965–981, 1992. a
Pleim, J. E.: A simple, efficient solution of flux-profile relationships in the atmospheric surface layer, J. Appl. Meteorol. Climatol., 45, 341–347, 2006. a
Pleim, J. E.: A combined local and nonlocal closure model for the atmospheric boundary layer. Part I: Model description and testing, J. Appl. Meteorol. Climatol., 46, 1383–1395, 2007. a, b, c
Pleim, J. E.: A combined local and nonlocal closure model for the atmospheric boundary layer. Part II: Application and evaluation in a mesoscale meteorological model, J. Appl. Meteorol. Climatol., 46, 1396–1409, 2007. a
Pleim, J. E. and Xiu, A. J.: Development of a land surface model. Part II: Data assimilation, J. Appl. Meteorol. Climatol., 42, 1811–1822, 2003. a
Rabier, F., Jarvinen, H., Klinker, E., Mahfouf, J. F., and Simmons, A.: The ECMWF operational implementation of four-dimensional variational assimilation. I: Experimental results with simplified physics, Q. J. Roy. Meteorol. Soc., 126, 1143–1170, 2000. a
Rayner, P., Enting, I., Francey, R., and Langenfelds, R.: Reconstructing the recent carbon cycle from atmospheric CO2, delta C-13 and O-2/N-2 observations, Tellus B, 51, 213–232, 1999. a
Rödenbeck, C., Houweling, S., Gloor, M., and Heimann, M.: CO2 flux history 1982–2001 inferred from atmospheric data using a global inversion of atmospheric transport, Atmos. Chem. Phys., 3, 1919–1964, https://doi.org/10.5194/acp-3-1919-2003, 2003. a
Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., Behringer, D., Hou, Y.-T., Chuang, H.-Y., Iredell, M., Ek, M., Meng, J., Yang, R., Mendez, M. P., Van Den Dool, H., Zhang, Q., Wang, W., Chen, M., and Becker, E.: The NCEP Climate Forecast System Version 2, J. Climate, 27, 2185–2208, 2014. a
Saito, R., Houweling, S., Patra, P. K., Belikov, D., Lokupitiya, R., Niwa, Y., Chevallier, F., Saeki, T., and Maksyutov, S.: TransCom satellite intercomparison experiment: Construction of a bias corrected atmospheric CO2 climatology, J. Geophys. Res., 116, d21120, https://doi.org/10.1029/2011JD016033, 2011. a
Schuh, A. E., Denning, A. S., Corbin, K. D., Baker, I. T., Uliasz, M., Parazoo, N., Andrews, A. E., and Worthy, D. E. J.: A regional high-resolution carbon flux inversion of North America for 2004, Biogeosciences, 7, 1625–1644, https://doi.org/10.5194/bg-7-1625-2010, 2010. a
Skamarock, W., Klemp, J., Dudhia, J., Gill, D., Barker, D., Duda, M., Huang, X., Wang, W., and Powers, J.: A description of the Advanced Research WRF version 3, NCAR Tech Note NCAR/TN-475+STR, https://doi.org/10.5065/D68S4MVH 2008. a, b
Smith, A., Lott, N., and Vose, R.: The Integrated Surface Database Recent Developments and Partnerships, B. Am. Meteorol. Soc., 92, 704–708, 2011. a
Stein, A. F., Draxler, R. R., Rolph, G. D., Stunder, B. J. B., Cohen, M. D., and Ngan, F.: NOAA'S HYSPLIT atmospheric transport and dispersion modeling system, B. Am. Meteorol. Soc., 96, 2059–2077, 2015. a, b
Stephens, B. B., Gurney, K. R., Tans, P. P., Sweeney, C., Peters, W., Bruhwiler, L., Ciais, P., Ramonet, M., Bousquet, P., Nakazawa, T., Aoki, S., Machida, T., Inoue, G., Vinnichenko, N., Lloyd, J., Jordan, A., Heimann, M., Shibistova, O., Langenfelds, R. L., Steele, L. P., Francey, R. J., and Denning, A. S.: Weak northern and strong tropical land carbon uptake from vertical profiles of atmospheric CO2, Science, 316, 1732–1735, 2007. a
Stohl, A., Forster, C., Frank, A., Seibert, P., and Wotawa, G.: Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2, Atmos. Chem. Phys., 5, 2461–2474, https://doi.org/10.5194/acp-5-2461-2005, 2005. a, b
Thompson, G., Field, P. R., Rasmussen, R. M., and Hall, W. D.: Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: implementation of a new snow parameterization, Mon. Weather Rev., 136, 5095–5115, 2008. a
Tremolet, Y.: Diagnostics of linear and incremental approximations in 4D-Var, Quart. J. Roy. Meteorol. Soc., 130, 2233–2251, 2004. a, b
Turner, A. J. and Jacob, D. J.: Balancing aggregation and smoothing errors in inverse models, Atmos. Chem. Phys., 15, 7039–7048, https://doi.org/10.5194/acp-15-7039-2015, 2015. a
Uliasz, M.: The Atmospheric Mesoscale Dispersion Modeling System, J. Appl. Meteorol., 32, 139–149, 1993. a, b
Yadav, V. and Michalak, A. M.: Improving computational efficiency in large linear inverse problems: an example from carbon dioxide flux estimation, Geosci. Model Dev., 6, 583–590, https://doi.org/10.5194/gmd-6-583-2013, 2013. a
Zhang, X., Huang, X.-Y., and Pan, N.: Development of the Upgraded Tangent Linear and Adjoint of the Weather Research and Forecasting (WRF) Model, J. Atmos. Oceanic Technol., 30, 1180–1188, 2013. a, b, c
Zheng, T., French, N., and Baxter, M.: WRF-CO2 4DVar assimilation system v1.0, https://doi.org/10.5281/zenodo.1220407, last access: 27 April 2018.
Zhu, C., Byrd, R., Lu, P., and Nocedal, J.: Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization, ACM Trans. Math. Software, 23, 550–560, 1997. a