the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
OMEN-SED 1.0: a novel, numerically efficient organic matter sediment diagenesis module for coupling to Earth system models
Sandra Arndt
Stuart Daines
Pierre Regnier
Andy Ridgwell
We present the first version of OMEN-SED (Organic Matter ENabled SEDiment model), a new, one-dimensional analytical early diagenetic model resolving organic matter cycling and the associated biogeochemical dynamics in marine sediments designed to be coupled to Earth system models. OMEN-SED explicitly describes organic matter (OM) cycling and the associated dynamics of the most important terminal electron acceptors (i.e. O2 , NO3, SO4) and methane (CH4), related reduced substances (NH4, H2S), macronutrients (PO4) and associated pore water quantities (ALK, DIC). Its reaction network accounts for the most important primary and secondary redox reactions, equilibrium reactions, mineral dissolution and precipitation, as well as adsorption and desorption processes associated with OM dynamics that affect the dissolved and solid species explicitly resolved in the model. To represent a redox-dependent sedimentary P cycle we also include a representation of the formation and burial of Fe-bound P and authigenic Ca–P minerals. Thus, OMEN-SED is able to capture the main features of diagenetic dynamics in marine sediments and therefore offers similar predictive abilities as a complex, numerical diagenetic model. Yet, its computational efficiency allows for its coupling to global Earth system models and therefore the investigation of coupled global biogeochemical dynamics over a wide range of climate-relevant timescales. This paper provides a detailed description of the new sediment model, an extensive sensitivity analysis and an evaluation of OMEN-SED's performance through comprehensive comparisons with observations and results from a more complex numerical model. We find that solid-phase and dissolved pore water profiles for different ocean depths are reproduced with good accuracy and simulated terminal electron acceptor fluxes fall well within the range of globally observed fluxes. Finally, we illustrate its application in an Earth system model framework by coupling OMEN-SED to the Earth system model cGENIE and tune the OM degradation rate constants to optimise the fit of simulated benthic OM contents to global observations. We find that the simulated sediment characteristics of the coupled model framework, such as OM degradation rates, oxygen penetration depths and sediment–water interface fluxes, are generally in good agreement with observations and in line with what one would expect on a global scale. Coupled to an Earth system model, OMEN-SED is thus a powerful tool that will not only help elucidate the role of benthic–pelagic exchange processes in the evolution and the termination of a wide range of climate events, but will also allow for a direct comparison of model output with the sedimentary record – the most important climate archive on Earth.
- Article
(12921 KB) -
Supplement
(126 KB) - BibTeX
- EndNote
Marine surface sediments are key components in the Earth system. They host the largest carbon reservoir within the surficial Earth system, provide the primary long-term sink for atmospheric CO2, recycle nutrients and represent the most important geochemical archive used for deciphering past changes in biogeochemical cycles and climate (e.g. Berner, 1991; Archer and Maier-Reimer, 1994; Ridgwell and Zeebe, 2005; Arndt et al., 2013). Physical and chemical processes in sediments (i.e. diagenetic processes) depend on the water column and vice versa: diagenesis is controlled by the external supply of solid material (e.g. organic matter, calcium carbonate, opal) from the water column and is affected by overlying bottom water concentrations of solutes. At the same time, sediments impact the water column directly either through the short- and long-term storage of deposited material or the diagenetic processing of deposited material and the transport of terminal electron acceptors (e.g. O2, SO4) into the sediments, as well as metabolic products (e.g. nutrients, DIC) to the overlying bottom waters. This so-called benthic–pelagic coupling is essential for understanding global biogeochemical cycles and climate (e.g. Archer and Maier-Reimer, 1994; Archer et al., 2000; Soetaert et al., 2000; Mackenzie, 2005).
The biological primary production of organic matter (OM, generally represented in its simple form CH2O in Reaction R1) and the reverse process of degradation can be written in a greatly simplified reaction as
On geological timescales, production of OM is generally greater than degradation, which results in some organic matter being buried in marine sediments and oxygen accumulating in the atmosphere. Thus, the burial of OM deep into the sediment leads to net oxygen input to and CO2 removal from the atmosphere (Berner, 2004). On shorter timescales, the upper few metres of the sediments where early diagenesis occurs are specifically important, as this zone controls whether a substance is recycled to the water column or buried for a longer period of time in the deeper sediments (Hensen et al., 2006). Most biogeochemical cycles and reactions in this part of marine sediments can be related either directly or indirectly to the degradation of organic matter (Middelburg et al., 1993; Arndt et al., 2013). Oxygen and nitrate, for instance, the highest energy-yielding electron acceptors, are preferentially consumed in the course of the degradation of organic matter, resulting in the release of ammonium and phosphorus to the pore water. As such, the degradation of OM in the sediments can profoundly affect the oxygen and nutrient inventory of the ocean and thus primary productivity (Van Cappellen and Ingall, 1994; Lenton and Watson, 2000). Furthermore, organic matter degradation releases metabolic CO2 to the pore water, causing it to have a lower pH and carbonate ion concentration, thus provoking the dissolution of calcium carbonate CaCO3 (Emerson and Bender, 1981).
Benthic nutrient recycling from marine sediments has been suggested to play a key role for climate and ocean biogeochemistry throughout Earth history. For example, feedbacks between phosphorus storage and erosion from shelf sediments and marine productivity have been hypothesised to play an important role for glacial–interglacial atmospheric CO2 changes (Broecker, 1982; Ruttenberg, 1993). Furthermore, benthic nutrient recycling from anoxic sediments has been invoked to explain the occurrence of more extreme events in Earth history, for instance oceanic anoxic events (OAEs; e.g. Van Cappellen and Ingall, 1994; Mort et al., 2007; Tsandev and Slomp, 2009). OAEs represent severe disturbances of the global carbon, oxygen and nutrient cycles of the ocean and are usually characterised by widespread bottom water anoxia and photic zone euxinia (Jenkyns, 2010). One way to explain the genesis and persistence of OAEs is increased oxygen demand due to enhanced primary productivity. Increased nutrient inputs to fuel primary productivity may in turn have come from marine sediments as the burial efficiency of phosphorus declines when bottom waters become anoxic (Ingall and Jahnke, 1994; Van Cappellen and Ingall, 1994). The recovery from OAE-like conditions is thought to involve the permanent removal of excess CO2 from the atmosphere and ocean by burying carbon in the form of organic matter in marine sediments (e.g. Arthur et al., 1988; Jarvis et al., 2011), which is consistent with the geological record of widespread black shale formation (Stein et al., 1986). Models capable of simulating not only the expansion and intensification of oxygen minimum zones, but also of predicting how the underlying sediments interact are hence needed.
Quantifications of diagenetic processes in the sediments are possible through the application of idealised mathematical representations, or so-called diagenetic models (see e.g. Berner, 1980; Boudreau, 1997). A plethora of different approaches have been developed, mainly following two distinct directions (see Arndt et al., 2013, for an overview). The first involves state-of-the-art vertically resolved numerical models simulating the entire suite of essential coupled redox and equilibrium reactions within marine sediments (e.g. BRNS, Aguilera et al., 2005; CANDI, Boudreau, 1996; MEDIA, Meysman et al., 2003; MUDS, Archer et al., 2002; STEADYSED, Van Cappellen and Wang, 1996). These “complete”, multi-component steady-state or non-steady-state models thus resolve the resulting characteristic redox zonation of marine sediments by explicitly accounting for oxic OM degradation, denitrification, oxidation by manganese and iron (hydr)oxides, sulfate reduction and methanogenesis as well as the reoxidation of reduced byproducts (i.e. NH4, Mn2+, Fe2+, H2S, CH4; see e.g. Regnier et al., 2011). Furthermore, they incorporate various mineral dissolution and precipitation reactions, as well as fast equilibrium sorption processes, for example of NH4, PO4 and metal ions (i.e. Mn2+, Fe2+ and Mg2+; compare Van Cappellen and Wang, 1996; Meysman et al., 2003). Modelled, depth-dependent transport processes usually comprise advection, diffusion, bioturbation and bio-irrigation. This group of diagenetic models generally describes OM degradation via a so-called multi-G approach (Jørgensen, 1978; Berner, 1980), thus dividing the bulk organic matter pool into a number of compound classes that are characterised by different degradabilities ki. Alternative approaches, so-called continuum models (Middelburg, 1989; Boudreau and Ruddick, 1991), assume a continuous distribution of reactive types but, although conceptually superior, are much less popular (Arndt et al., 2013). These complex, multi-component models have great potential for quantifying diagenetic dynamics at sites where comprehensive observational datasets are available to constrain its model parameters (see e.g. Boudreau et al., 1998; Wang and Van Cappellen, 1996; Thullner et al., 2009, for applications). However, due to the high degree of coupled processes and depth-varying parameters, the diagenetic equation needs to be solved numerically, thus resulting in a very high computational demand and consequently rendering their application in an Earth system model (ESM) framework with a large number of grid points prohibitive. Additionally, their global applicability is seriously compromised by the restricted transferability of model parameters from one site to the global scale (Arndt et al., 2013).
The second group of diagenetic models emerged during the early days of diagenetic modelling when computing power was severely restricted (e.g. Berner, 1964). These models solve the diagenetic equation analytically, thus providing an alternative and computationally more efficient approach. Finding an analytical solution, especially when complex reaction networks are to be considered, is not straightforward and analytical models are thus usually less sophisticated and comprehensive than numerical models and generally require the assumption of steady-state conditions. It has been shown that the complexity of the reaction network can be reduced by dividing the sediment column into distinct zones and accounting for the most pertinent biogeochemical processes within each zone, thus increasing the likelihood of finding an analytical solution without oversimplifying the problem. Analytical approaches with distinct biogeochemical zones were implemented and used in the 1970s and 1980s to describe observed pore water profiles (e.g. Vanderborght and Billen, 1975; Vanderborght et al., 1977; Billen, 1982; Goloway and Bender, 1982; Boudreau and Westrich, 1984) and later for inclusion into multi-box ecosystem models (e.g. Ruardij and Van Raaphorst, 1995; Gypens et al., 2008) and global Earth system models (Tromp et al., 1995). However, in addition to the oxic zone these models generally only describe one anoxic zone explicitly, either a denitrification (Vanderborght and Billen, 1975; Billen, 1982; Goloway and Bender, 1982; Ruardij and Van Raaphorst, 1995; Gypens et al., 2008) or a sulfate reduction zone (Boudreau and Westrich, 1984; Tromp et al., 1995). Furthermore, the approaches of Vanderborght and Billen (1975), Goloway and Bender (1982) and Tromp et al. (1995) do not explicitly account for reduced species (i.e. NH4 and H2S).
In most current ESMs sediment–water dynamics are either neglected or treated in a very simplistic way (Soetaert et al., 2000; Hülse et al., 2017). Most Earth system models of intermediate complexity (EMICs) and also some of the higher-resolution Earth system–climate models represent the sediment–water interface either as a reflective or a conservative–semi-reflective boundary (Hülse et al., 2017). Thus, all particulate material deposited on the sea floor is either instantaneously consumed (reflective boundary), or a fixed fraction is buried in the sediments (conservative–semi-reflective boundary). Both highly simplified approaches furthermore completely neglect the exchange of solute species through the sediment–water interface and therefore cannot resolve the complex benthic–pelagic coupling. However, due to their computational efficiency, both representations are often used in global biogeochemical models (e.g. Najjar et al., 2007; Ridgwell et al., 2007; Goosse et al., 2010). Analytical diagenetic models represent the most complex description of diagenetic dynamics in Earth system models. Examples of global ESMs employing a vertically resolved diagenetic model are NorESM (Tjiputra et al., 2013) and HAMOCC (Palastanga et al., 2011; Ilyina et al., 2013), both using a version of Heinze et al. (1999). None of the EMICs reviewed by Hülse et al. (2017) use such a sediment representation. DCESS (Shaffer et al., 2008) and MBM (Munhoven, 2007) are box models employing a vertically resolved diagenetic model. These analytic models account for the most important transport processes (i.e. advection, bioturbation and molecular diffusion) through basic parameterisations and include fewer biogeochemical reactions, which are generally restricted to the upper, bioturbated 10 cm of the sediments. Pore water species explicitly represented in DCESS (Shaffer et al., 2008) and the HAMOCC model of Heinze et al. (1999) and Palastanga et al. (2011) are restricted to DIC, TA, PO4 and O2. The MEDUSA model (Munhoven, 2007) considers CO2, , and O2. Other species produced or consumed during OM degradation are neglected. Thus, with oxygen being the only TEA explicitly modelled, the influence of reduced species is only implicitly included in the boundary conditions for O2. A newer version of the HAMOCC model is a notable exception, as Ilyina et al. (2013) include NO3 and denitrification explicitly. Furthermore, the version of Palastanga et al. (2011) represents a redox-dependent explicit sedimentary phosphorus cycle. Yet, the reoxidation of reduced byproducts, so-called secondary redox reactions (e.g. oxidation of NH4, H2S or CH4), or sorption processes are not included in any of the discussed models. Furthermore, these global models assume that the sedimentary organic matter pool is composed of just a single compound class which is either degraded with a globally invariant degradation rate constant (Munhoven, 2007) or a fixed rate constant depending on local oxygen concentrations (Shaffer et al., 2008; Palastanga et al., 2011).
Obviously, such a simplification of the OM pool can neither account for the observed vast structural complexity in natural organic matter and its resulting different degradation rates nor for the rapid decrease in OM degradability in the uppermost centimetres of the sediments (Arndt et al., 2013). It has been suggested that at least a 3G approach is necessary to accurately represent organic matter dynamics in this part of the sediments where most OM is degraded (e.g. Soetaert et al., 1996). Even more restrictive is the use of O2 as the only TEA and the complete absence of reduced substances and related secondary redox reactions. For the majority of the modern sediments (i.e. in the deep ocean) O2 is the primary electron acceptor; however, recent model and data studies have reported that sulfate reduction is the dominant degradation pathway on a global average (with contributions of 55–76 % Canfield et al., 2005; Jørgensen and Kasten, 2006; Thullner et al., 2009). Oxygen becomes progressively less important as TEA with decreasing sea-floor depth and sulfate reduction has been shown to account for 83 % of OM degradation in coastal sediments (Krumins et al., 2013). In these environments most O2 is used to reoxidise reduced substances produced during anaerobic degradation (Canfield et al., 2005; Thullner et al., 2009). Thus, the in situ production of e.g. NO3 and SO4 through the oxidation of NH4 and H2S forms an important sink for O2 which is entirely neglected in current sediment representations in global models. In addition, the lack of anoxic degradation pathways in these models limits their application to oxic oceans. Currently no analytical sediment model exists that can be used under anoxic conditions. Due to the lack of an appropriate sedimentary P cycle (with the exception of the HAMOCC version of Palastanga et al., 2011), no current global ESM is able to model the redox-dependent P release from marine sediments and its implications for primary productivity, global biogeochemical cycles and climate. A sediment model suitable for coupling to an ESM and enabling a wide range of paleo-questions to be addressed has to provide a robust quantification of organic (and inorganic) carbon burial fluxes, benthic uptake and return fluxes of oxygen, growth-limiting nutrients and reduced species, as well as anoxic degradation pathways. As a consequence, the reaction network must account for the most important primary and secondary redox reactions, equilibrium reactions, mineral precipitation and dissolution, and adsorption and desorption, resulting in a complex set of coupled reaction–transport equations.
Therefore, we developed the Organic Matter ENabled SEDiment model (OMEN-SED), a new, one-dimensional, numerically efficient diagenetic model. OMEN-SED builds upon and stands in the tradition of earlier stand-alone, analytical diagenetic models (Vanderborght et al., 1977; Billen, 1982; Goloway and Bender, 1982; Boudreau, 1991) and analytical diagenetic models developed for coupling to regional-scale ecosystem or global Earth system models (Ruardij and Van Raaphorst, 1995; Tromp et al., 1995; Heinze et al., 1999; Gypens et al., 2008).
OMEN-SED is the first analytical model to explicitly describe OM cycling and the associated dynamics of the most important TEAs (i.e. O2, NO3, SO4), related reduced substances (NH4, H2S), the full suite of secondary redox reactions, macronutrients (PO4) and the associated pore water quantities (ALK, DIC). To represent a redox-dependent sedimentary P cycle we consider the formation and burial of Fe-bound P and authigenic Ca–P minerals. Thus, while OMEN-SED captures most of the features of a complex, numerical diagenetic model, its computational efficiency allows for coupling to global Earth system models and therefore the investigation of coupled global biogeochemical dynamics over different timescales. Here, the model is presented as a 2G approach; however, OMEN-SED can be easily extended to a multi-G approach. The first part of the paper provides a detailed description of OMEN-SED (Sect. 2). This includes descriptions of the general model approach (Sect. 2.1), the conservation equations for all explicitly represented biogeochemical tracers (Sect. 2.2) and a summary of global relationships used to constrain reaction and transport parameters in OMEN-SED (Sect. 2.4). In addition, a generic algorithm is described which is used to match internal boundary conditions and to determine the integration constants for the analytical solutions (Sect. 2.3). In order to validate the stand-alone version of OMEN-SED, the second part of the paper performs an extensive sensitivity analysis for the most important model parameters, and resulting sediment–water interface fluxes are compared with a global database (Sect. 3.1). In addition, the results of the stand-alone model are compared with observed pore water profiles from different ocean depths (Sect. 3.2), and OMEN-SED simulations of TEA fluxes along a typical ocean transect are compared with observations and results from a complete, numerical diagenetic model (Sect. 3.3). Thereafter, OMEN-SED is coupled to the carbon-centric version of the GENIE Earth system model (cGENIE; Ridgwell et al., 2007, Sect. 4.1). Sensitivity studies are carried out using this coupled model and modelled organic matter concentrations in the surface sediments are compared to a global database (Seiter et al., 2004, Sect. 4.2). We finally discuss potential applicabilities of OMEN-SED and critically analyse model limitations (Sect. 5).
OMEN-SED is implemented as a FORTRAN version that can be easily coupled to any pelagic, biogeochemical model via the coupling routine OMEN_SED_main. In addition, OMEN-SED exists as a stand-alone version implemented in MATLAB and the entire model can be executed on a standard personal computer in less than 0.1 s. The source code of both the FORTRAN and the MATLAB stand-alone version and instructions for executing OMEN-SED and for plotting model results are available as a Supplement to this paper.
The following section provides a detailed description of OMEN-SED and the fundamental equations underlying the model are highlighted. Tables 1 and A1 summarise the biogeochemical reaction network and Tables 9 and 10 provide a glossary of model parameters along with their respective units.
2.1 General model approach
In OMEN-SED, the calculation of benthic uptake, recycling and burial fluxes is based on the vertically resolved conservation equation for solid and dissolved species in porous media (e.g. Berner, 1980; Boudreau, 1997):
where Ci is the concentration of biogeochemical species i, and ξ equals the porosity ϕ for solute species and (1−ϕ) for solid species. The term z is the sediment depth, t denotes the time, Di is the apparent diffusion coefficient of species i, w is the advection rate and represents the sum of all biogeochemical rates j affecting species i.
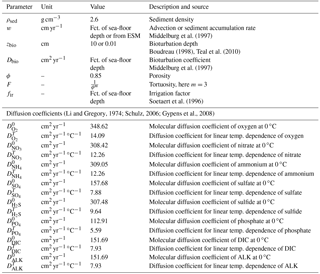
OMEN-SED accounts for both the advective and the diffusive transport of solid and dissolved species. They are buried in the sediment according to a constant advection rate w, thus neglecting the effect of sediment compaction (i.e. ) due to mathematical constraints. The molecular diffusion of dissolved species is described by Fick's law applying a species-specific apparent diffusion coefficient, Dmol,i. In addition, the activity of infaunal organisms in the bioturbated zone is simulated using a diffusive term (e.g. Boudreau, 1986), with a constant bioturbation coefficient Dbio in the bioturbated zone, while Dbio is set to zero below the maximum bioturbation depth, zbio. The pumping activity by burrow-dwelling animals and the resulting ventilation of tubes, the so-called bio-irrigation, is encapsulated in a factor fir that enhances the molecular diffusion coefficient (hence, ; Soetaert et al., 1996). The reaction network of OMEN-SED accounts for the most important primary and secondary redox reactions, equilibrium reactions, mineral dissolution and precipitation, and the adsorption and desorption processes associated with OM dynamics that affect the dissolved and solid species explicitly resolved in the model. Tables 1 and A1 provide a summary of the reactions and biogeochemical tracers considered in OMEN-SED together with their respective reaction stoichiometries.
Table 1Reactions and biogeochemical tracers implemented in the reaction network of OMEN-SED. The primary and secondary redox reactions are listed in the sequence they occur with increasing sediment depth.

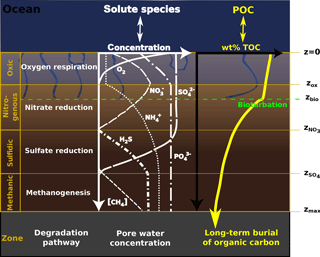
All parameters in Eq. (1), apart from porosity and burial rate, may vary with sediment depth and many reaction rate expressions depend on the concentration of other species. Expressing Eq. (1) for a set of chemical species thus results in a non-linear, coupled set of equations that can only be solved numerically. However, OMEN-SED is designed for coupling to Earth system models and therefore cannot afford a computationally expensive numerical solution. Instead, similar to early analytical diagenetic models, a computationally efficient analytical solution to Eq. (1) can be derived by (1) assuming steady-state conditions (i.e.) and (2) reducing the vertical variability in parameters and reaction rate expressions by dividing the sediment column into a number of functional biogeochemical zones (Fig. 1; compare e.g. Billen, 1982; Goloway and Bender, 1982; Ruardij and Van Raaphorst, 1995; Tromp et al., 1995; Gypens et al., 2008, for similar solutions). More specifically, OMEN-SED follows Berner (1980) by dividing the sediment column into (I) a bioturbated and (II) a non-bioturbated zone defined by an imposed, constant bioturbation depth zbio (Fig. 1). Furthermore, it resolves the dynamic redox stratification of marine sediments by dividing the sediment into (1) an oxic zone delineated by the oxygen penetration depth zox; (2) a denitrification (or nitrogenous) zone situated between zox and the nitrate penetration depth ; (3) a sulfate reduction zone situated between and the sulfate penetration depth ; and (4) a methanogenic zone situated below (Fig. 1). Although in each of these zones Eq. (1) is applied with depth invariant parameters, parameter values may differ across zones. The biogeochemical zones are linked by stating continuity in both concentrations and fluxes at the dynamic, internal boundaries (; compare e.g. Billen, 1982; Ruardij and Van Raaphorst, 1995). Note that these boundaries are dynamic because their depth varies in response to changing ocean boundary conditions and forcings (see Sect. 2.3.1 for details). Furthermore, the maximum bioturbation depth is not restricted to a specific biogeochemical zone, and hence OMEN-SED allows bioturbation to occur in the anoxic zones of the sediment (here all zones z>zox combined).
The formulation of the reaction term in Eq. (1) varies between zones and encapsulates the most pertinent reaction processes within the respective zone (see Sect. 2.2), thus simplifying the mathematical description of the reaction network while retaining most of its biogeochemical complexity. One such simplification is that solid-phase iron and manganese oxidants and their reductants are not considered in the reaction network. All consumption and production processes of dissolved species related to the degradation of organic matter are a function of the organic matter concentration. Because organic matter degradation is described as a first-order degradation, these processes can be expressed as a series of exponential terms (; see Eq. 2). In addition, slow adsorption and desorption and mineral precipitation processes can be expressed as zero- or first-order (reversible) reactions (Qm or kl⋅Ci in Eq. 2). Fast adsorption is described as an instantaneous equilibrium reaction using a constant adsorption coefficient Ki. The reoxidation of reduced substances is accounted for implicitly by adding a (consumption and production) flux to the internal boundary conditions (see Sect. 2.2.2, 2.2.3 and 2.2.4). This simplification has been used previously by Gypens et al. (2008) for nitrate and ammonium and can be justified as it has been shown that reoxidation mainly occurs within a thin layer at the oxic–anoxic interface (Soetaert et al., 1996). The general reaction–transport equation underlying OMEN-SED is thus given by
where 1∕βj can be interpreted as the length scale and αj as
the relative importance (or the magnitude at z=0) of reaction j
(Boudreau, 1997);
kl represents generic first-order reaction rate constants and Qm represents zero-order (or constant) reaction rates.
The analytical solution to Eq. (2) is of the general form
with
where A and B are integration constants that can be determined by applying a set of internal boundary conditions (see Sect. 2.3) and .
Based on Eq. (2) and its analytical solution Eq. (3), OMEN-SED returns the fraction of particulate organic carbon (POC) buried in the sediment, fPOC, and the benthic uptake and return fluxes of dissolved species Ci (in mol cm−2 yr−1) in response to the dynamic interplay of transport and reaction processes under changing boundary conditions and forcings:
where w is the deposition rate, Di is the diffusion coefficient and POC(0), POC(zmax) and Ci(0) denote the concentration of POC and dissolved species i at the sediment–water interface (SWI) and at the lower sediment boundary, respectively.
2.2 Conservation equations and analytical solution
The following sections provide a detailed description of the conservation equations and analytical solutions for each chemical species that is resolved in this version of OMEN-SED.
2.2.1 Organic matter or particulate organic carbon (POC)
In marine sediments, organic matter (or in the following called particulate organic carbon, POC) is degraded by heterotrophic activity coupled to the sequential utilisation of terminal electron acceptors (TEAs) according to the free energy gain of the half-reaction (; e.g. Stumm and Morgan, 2012). Once all TEAs are depleted, organic matter is degraded via methanogenesis. Here, organic matter degradation is described via a multi-G model approach (Jørgensen, 1978), dividing the bulk OM into a number i of discrete compound classes POCi characterised by class-specific first-order degradation rate constants ki. The conservation equation for organic matter dynamics is thus given by
with for z≤zbio and for z>zbio. Integration of Eq. (7) yields the following general solutions for the bioturbated and non-bioturbated layers.
In the above equations,
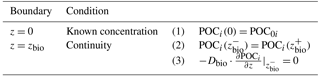
Determining the integration constants () requires the definition of a set of boundary conditions (Table 2). For organic matter, OMEN-SED applies a known concentration at the sediment–water interface and assumes continuity across the bottom of the bioturbated zone, zbio. When OMEN-SED is coupled to an ESM, the POC depositional flux from the coupled ocean model is converted to a concentration by solving the flux divergence Eq. (51). The integration constants () are thus given by the following.
See Sect. 2.3.1 for further details on how to find the analytical solution.
2.2.2 Oxygen
OMEN-SED explicitly accounts for oxygen consumption by the aerobic degradation of organic matter within the oxic zone and the oxidation of reduced species (i.e. NH4, H2S) produced in the anoxic zones of the sediment. In the oxic zone (z<zox), aerobic degradation consumes oxygen with a fixed O2:C ratio (O2C, Table 10). A predefined fraction, , of the ammonium produced during the aerobic degradation of OM is nitrified to nitrate, consuming 2 moles of oxygen per mole of ammonium produced. In addition, OMEN-SED implicitly accounts for oxygen consumption due to the oxidation of reduced species (NH4, H2S) produced below the oxic zone through the flux boundary condition at the dynamically calculated oxygen penetration depth zox (see Sect. 2.4.2 for details). All oxygen consumption processes can thus be formulated as a function of organic matter degradation. The conservation equation for oxygen is given by
For illustrative purposes, we here substitute the analytical solution for the POC depth profile and provide the analytical solution. The remaining paragraphs only outline the general equation, whose analytical solution can be derived in an identical manner. Substituting Eqs. (8) and (9) for POCi(z) and Eq. (11) for B1i gives the following.
and denote the O2 diffusion coefficient for the bioturbated and non-bioturbated zone, respectively. The term accounts for the volume conversion from solid to dissolved phase and NCi is the nitrogen to carbon ratio in POC. Integration yields the following analytical solution for each zone.
with
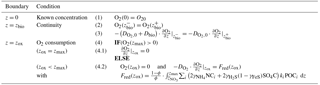
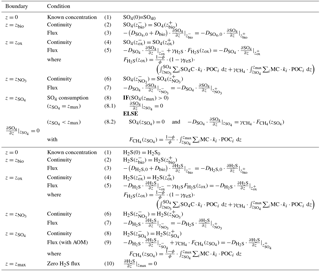
Determining the four integration constants (; see Sect. 2.3 for details) and the a priori unknown oxygen penetration depth requires the definition of five boundary conditions (see Table 3). At the sediment–water interface, OMEN-SED applies a Dirichlet condition (i.e. known concentration) and assumes concentration and flux continuity across the bottom of the bioturbated zone, zbio. The oxygen penetration depth zox marks the lower boundary and is dynamically calculated as the depth at which O2(z)=0. Therefore, OMEN-SED applies a Dirichlet boundary condition O2(zox)=0. In addition, a flux boundary is applied that implicitly accounts for the oxygen consumption by the partial oxidation of NH4 and H2S diffusing into the oxic zone from below (BC 4.2; Table 3). It is assumed that respective fractions ( and ) are directly reoxidised at the oxic–anoxic interface and the remaining fraction escapes reoxidation (or is precipitated as pyrite, γFeS). OMEN-SED iteratively solves for zox by first testing if there is oxygen left at zmax (i.e. O2(zmax)>0). If that is not the case, it determines the root for the flux boundary condition 4.2 (Table 3). If zox=zmax, a zero diffusive flux boundary condition is applied as a lower boundary condition.
2.2.3 Nitrate and ammonium
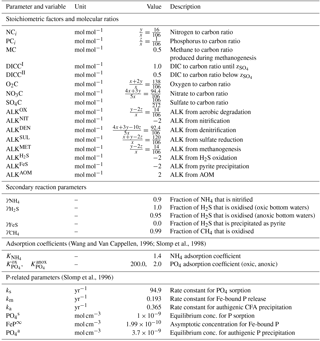
Nitrogen dynamics in OMEN-SED are controlled by the metabolic production of ammonium, nitrification, denitrification and ammonium adsorption. Ammonium is produced by organic matter degradation in both the oxic and anoxic zones, while denitrification consumes nitrate in the denitrification zone with a fixed NO3:C ratio (NO3C; Table 10). Anaerobic ammonium oxidation (anammox) is implicitly included in the model. The organic nitrogen released during denitrification is assumed to be directly oxidised with nitrite to N2 through a coupling between denitrification and anammox.
The adsorption of ammonium to sediment particles is formulated as an equilibrium process with a constant equilibrium adsorption coefficient , thus assuming that the adsorption is fast compared to the characteristic timescales of transport processes (Wang and Van Cappellen, 1996). In addition, a defined fraction, , of metabolically produced ammonium is directly nitrified to nitrate in the oxic zone, while the nitrification of upward-diffusing ammonium produced in the sulfidic and methanic zones is implicitly accounted for in the boundary conditions. The conservation equations for ammonium and nitrate are thus given by the following.
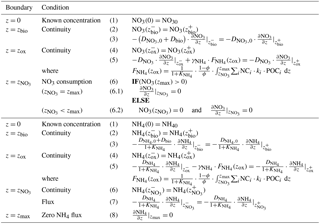
and denote the diffusion coefficients for NO3 and NH4, which depend on the bioturbation status of the respective geochemical zone (compare to Sect. 2.3.1). Integration of Eqs. (15)–(19) yields the analytical solutions, which are not further developed here but follow the procedure outlined in Sect. 2.2.2 for oxygen (also see Sect. 2.3.1 for more details on how to find the analytical solution). Table 4 summarises the boundary conditions applied in OMEN-SED to solve Eqs. (15)–(19) and to find the a priori unknown nitrate penetration depth, . The model assumes known bottom water concentrations for both NO3 and NH4, the complete consumption of nitrate at the nitrate penetration depth (in the case ) and no change in ammonium flux at zmax. In addition, concentration and diffusive flux continuity across zbio and zox is considered for NO3 and NH4. Furthermore, the reoxidation of upward-diffusing reduced ammonium is accounted for in the oxic–anoxic boundary condition for nitrate and ammonium. OMEN-SED iteratively solves for by first testing if there is nitrate left at zmax (i.e. NO3(zmax)>0) and otherwise by finding the root for the flux boundary condition 6.2 (Table 4).
2.2.4 Sulfate and sulfide
Below the denitrification zone (), organic matter degradation is coupled to sulfate reduction, consuming sulfate and producing hydrogen sulfide with a fixed SO4:C ratio (SO4C; Table 10). In addition, the anaerobic oxidation of upward-diffusing methane (AOM) produced below the sulfate penetration and the associated consumption of sulfate and production of sulfide, as well as the production of sulfate and consumption of sulfide through sulfide oxidation, are implicitly accounted for through the boundary conditions (Table 5). In the sulfidic zone a defined fraction of sulfide, γFeS, can be precipitated as pyrite (in the presented simulations γFeS=0.0 as we do not want to make any assumptions about pyrite precipitation). It can be safely assumed that almost all CH4 is oxidised anaerobically in the sediments (e.g. Reeburgh, 2007, suggests up to 90 %), except for active (very localised) sites and slope failure, which can, in theory, be accounted for through the term. The conservation equations for sulfate and sulfide are thus given by the following.
and denote the diffusion coefficients for SO4 and H2S, which depend on the bioturbation status of the respective geochemical zone (compare to Sect. 2.3.1). Integration of Eqs. (20)–(24) yields the analytical solution and Table 5 summarises the boundary conditions applied. OMEN-SED assumes known concentrations at the sediment–water interface and continuity across the bioturbation depth and the nitrate penetration depth. The reoxidation of reduced H2S to SO4 is accounted for implicitly via the oxic–anoxic boundary condition for both species, while the reduction of SO4 and the associated production of H2S via AOM is accounted for through the respective boundary conditions at . In the case , OMEN-SED assumes zero sulfate concentration at and its diffusive flux must equal the amount of methane produced below (with a methane to carbon ratio of MC); in the case , a zero diffusive flux condition for sulfate is considered. OMEN-SED iteratively solves for by first testing if there is sulfate left at zmax (i.e. SO4(zmax)>0) and otherwise by finding the root for the flux boundary condition 8.2 (Table 5). At the lower boundary zmax zero diffusive flux of H2S is considered.
2.2.5 Phosphate
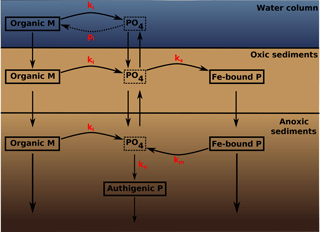
Figure 2A schematic of the sedimentary P cycle in OMEN-SED. Red numbers represent kinetic rate constants for phosphorus dynamics (compare to Table 10; pi represents the uptake rate of PO4 via primary production in shallow environments). Adapted from Slomp et al. (1996).
The biogeochemical description of phosphorus (P) dynamics builds on earlier models developed by Slomp et al. (1996) and accounts for phosphorus recycling through organic matter degradation, adsorption onto sediments and iron(III) hydroxides (Fe-bound P), as well as carbonate fluorapatite (CFA or authigenic P) formation (see Fig. 2 for a schematic overview of the sedimentary P cycle). In the oxic zone of the sediment, PO4 liberated through organic matter degradation can adsorb to iron(III) hydroxides forming Fe-bound P (or FeP; Slomp et al., 1998). Below the oxic zone, PO4 is not only produced via organic matter degradation but can also be released from the Fe-bound P pool due to the reduction of iron(III) hydroxides under anoxic conditions. Furthermore, in these zones phosphate concentrations build up and pore waters can thus become supersaturated with respect to carbonate fluorapatite, thus triggering the authigenic formation of CFA (Van Cappellen and Berner, 1988). Phosphorus bound in these authigenic minerals represents a permanent sink for reactive phosphorus (Slomp et al., 1996). As for ammonium, the adsorption of P to the sediment matrix is treated as an equilibrium process parameterised with dimensionless adsorption coefficients for the oxic and anoxic zone, respectively (, ; Slomp et al., 1998). The adsorption and desorption of P to iron(III) hydroxides and authigenic fluorapatite formation are described as first-order reactions with rate constants ks, km and ka, respectively (Table 10). The rate of the respective process is calculated as the product of the rate constant and the difference between the current concentration (of PO4 and FeP) and an equilibrium or asymptotic concentration (Slomp et al., 1996). The asymptotic Fe-bound P concentration is FeP∞ and the equilibrium concentrations for P sorption and authigenic fluorapatite formation are and , respectively (Table 10). The last term in Eqs. (25) and (26) represents the sorption of PO4 to FeP in the oxic zone, the last term in Eqs. (27) and (28) is the release of PO4 from the FeP pool and the fourth term in Eq. (28) represents the permanent loss of PO4 to authigenic fluorapatite formation. The conservation equations for phosphate and Fe-bound P are thus given by the following.
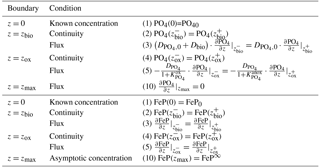
denotes the diffusion coefficient for PO4, which depends on the bioturbation status of the respective geochemical zone, and DFeP=Dbio for z≤zbio and DFeP=0 for z>zbio (compare to Sect. 2.3.1). Integration of Eqs. (25)–(28) yields the analytical solution and Table 6 summarises the boundary conditions applied in OMEN-SED. The model assumes known bottom water concentrations and equal concentrations and diffusive fluxes at zbio and zox for both species. Additionally, OMEN-SED considers no change in phosphate flux and an asymptotic Fe-bound P concentration at zmax.
2.2.6 Dissolved inorganic carbon (DIC)
OMEN-SED accounts for the production of dissolved inorganic carbon (DIC) through organic matter degradation and methane oxidation. Organic matter degradation produces dissolved inorganic carbon with a stoichiometric DIC:C ratio of 1:2 in the methanic zone and 1:1 in the rest of the sediment column (DICCII and DICCI, respectively). DIC production through methane oxidation is implicitly taken into account through the boundary condition at . A mechanistic description of DIC production from CaCO3 dissolution would lead to significant mathematical problems and is therefore not included in the current version of OMEN-SED. The conservation equations for DIC are thus given by the following.
DDIC denotes the diffusion coefficient for DIC (taking the values for from Schulz, 2006), which depends on the bioturbation status of the respective geochemical zone. Integration of Eqs. (29) and (30) yields the analytical solution and Table 7 summarises the boundary conditions applied in OMEN-SED. A Dirichlet condition is applied at the sediment–water interface. In addition, the model assumes a zero diffusive flux through the lower boundary zmax and continuity across the bottom of the bioturbated zone and the sulfate penetration depth. An additional flux boundary condition at implicitly accounts for DIC production through the anaerobic oxidation of methane (Table 7 Eq. 5).
2.2.7 Alkalinity
Organic matter degradation and secondary redox reactions exert a complex influence on alkalinity (e.g. Jourabchi et al., 2005; Wolf-Gladrow et al., 2007; Krumins et al., 2013). To model alkalinity, OMEN-SED divides the sediment column into four geochemical zones in which different equations describe the biogeochemical processes using variable stoichiometric coefficients (compare values in Table 10). Above zox, the combined effects of NH4 and P release due to aerobic OM degradation increases alkalinity according to ALKOX, whereas nitrification decreases alkalinity with stoichiometry ALKNIT. In the remaining three zones anaerobic OM degradation generally results in an increase in alkalinity, with the exact magnitude depending on the nature of the terminal electron acceptor used (i.e. ALKDEN, ALKSUL, ALKMET). In addition, the effect of secondary redox reactions, such as nitrification, sulfide and methane oxidation, and pyrite precipitation are implicitly accounted for in the boundary conditions. Note that the alkalinity description in the current version of OMEN-SED does not account for CaCO3 dissolution and precipitation due to the mathematical complexity of the problem. In OMEN-SED, the conservation equations for alkalinity are thus given by the following.
DALK denotes the diffusion coefficient for alkalinity (taking the values for from Schulz, 2006), which depends on the bioturbation status of the respective geochemical zone. Integration of Eqs. (31)–(34) yields the analytical solution and Table 8 summarises the boundary conditions applied in OMEN-SED. A Dirichlet boundary condition is applied at the sediment–water interface. The decrease in alkalinity due to the oxidation of reduced species produced in the anoxic zones and due to the precipitation of pyrite (with stoichiometry ALKNIT, and ALKFeS) is implicitly taken into account through the flux boundary condition at zox (Table 8 Eq. 5). Furthermore, the oxidation of methane by sulfate reduction increases alkalinity with stoichiometry ALKAOM, which is accounted for through the flux boundary condition at (Table 8 Eq. 9). At the lower boundary zmax a zero diffusive flux condition is applied.
2.3 Determination of integration constants
The integration constants of all general analytical solutions derived above change in response to changing boundary conditions. Thus, OMEN-SED has to redetermine integration constants for each dynamic zone (i.e. and ) at every time step for all biogeochemical species. The bioturbation boundary poses a particular challenge as it can theoretically occur in any of the dynamic geochemical zones (Fig. 3). Therefore, in order to generalise and simplify this recurring boundary matching problem, an independent, generic algorithm (generic boundary condition matching) is implemented (rather than using multiple fully-worked-out algebraic solutions for each possible case and every biogeochemical species). As a consequence, the algorithm only has to solve a two-simultaneous-equation problem.
2.3.1 Generic boundary condition matching (GBCM)
As discussed in Sect. 2.1, the solution to the general steady-state transport-reaction equation (Eq. 2) for a generic species C is of the general form
and can therefore be expressed as
where E(z) and F(z) are the homogeneous solutions to the ODE, G(z) the particular integral (collectively called the basis functions), and A and B are the integration constants that must be determined using the boundary conditions (shown in Fig. 3 for the whole sediment column).
Each internal boundary matching problem (i.e. excluding z=0 and z=zmax) involves matching continuity and flux for the two solutions to the respective reaction–transport equation above (CU(z) “upper”) and below (CL(z) “lower”) the dynamic boundary at z=zb.
OMEN-SED generally applies concentration continuity and flux boundary conditions at its internal dynamic boundaries.
Continuity (where for generality we allow a discontinuity Vb):
where w is advection, D represents the diffusion coefficients and Fb is any flux discontinuity (e.g. resulting from secondary redox reactions). Considering that the advective flux above and below the boundary is equal (i.e. wCU(zb)=wCL(zb)) and substituting the general ODE solutions (37) and (38), the boundary conditions can be represented as two equations connecting the four integration constants:
where the ODE solutions E, F and G are all evaluated at zb. Equation (41) can now be solved to give AU and BU as a function of the integration constants from the layer below (AL and BL), thereby constructing a piecewise solution for both layers with just two integration constants (this is implemented in the function benthic_utils.matchsoln of OMEN-SED):
Using Eq. (42), CU(z) in Eq. (37) can now be rewritten as a function of AL and BL (implemented in benthic_utils.xformsoln):
and hence the “transformed” basis functions and can be defined such that
where

Figure 3Schematic of the generic boundary condition matching (GBCM) problem. Shown are the resulting integration constants (Ai, Bi) and ODE solutions () for the different sediment layers and the bioturbation boundary (possible locations are indicated by the green vertical arrow).
Equations (42), (44) and (45) can now be consecutively applied for each of the dynamic biogeochemical zone boundaries (Fig. 3) starting at the bottom of the sediment column. The net result is a piecewise solution for the whole sediment column with just two integration constants (coming from the lowest layer), which can then be solved for by applying the boundary conditions at the sediment–water interface and the bottom of the sediments.
2.3.2 Abstracting out the bioturbation boundary
The bioturbation boundary affects the diffusion coefficient of the modelled solutes and the conservation equation of organic matter (and thereby the exact form of each reaction–transport equation). This boundary is particularly inconvenient as it can in principle occur in the middle of any of the dynamically shifting biogeochemical zones and therefore generate multiple cases (Fig. 3). The GBCM algorithm described above is thus not only used to construct a piecewise solution for the whole sediment column, but also to abstract out the bioturbation boundary. For each biogeochemical zone the “bioturbation status” is initially tested (i.e. fully bioturbated, fully non-bioturbated or crossing the bioturbation boundary). Therefore, the upper and lower boundaries for the different zones (e.g. for the nitrogenous zone zU=zox, ) and the respective reactive terms and diffusion coefficients (bioturbated and non-bioturbated) are passed over to the routine zTOC.prepfg_l12 in which the bioturbation status is determined. In the case that the bioturbation depth is located within this zone (i.e. ) a piecewise solution for this layer is constructed. Therefore, the reactive terms and diffusion coefficients are handed over to the routines zTOC.calcfg_l1 and zTOC.calcfg_l2, which calculate the basis functions ( and ) and their derivatives for the bioturbated and the non-bioturbated part of this specific geochemical zone. The concentration and flux for both solutions at zbio are matched and the coefficients and d2 (as in Eq. 42) are calculated by the routine benthic_utils.matchsoln. These coefficients and the “bioturbation status” of the layer are passed back to the main GBCM algorithm in which they can be used by the routine benthic_utils.xformsoln to calculate the “transformed” basis functions () such that both layers are expressed in the same basis (compare Eqs. 43–45).
For instance, in the case of sulfate, zTOC.prepfg_l12 is called three times before the actual profile is calculated (once per zone: oxic, nitrogenous, sulfidic) and hands back the information about the “bioturbation status” of the three layers and the coefficients and d2 for the biogeochemical zone including the bioturbation depth. When calculating the complete piecewise solution for the sediment column, this information is passed to the function zTOC.calcfg_l12, which sorts out the correct solution type to use. The main GBCM algorithm therefore never needs to know whether it is dealing with a piecewise solution (i.e. matched across the bioturbation boundary) or a “simple” solution (i.e. the layer is fully bioturbated or fully non-bioturbated).
2.4 Model parameters
The following section provides a summary of global relationships used to constrain reaction and transport parameters in OMEN-SED. Table 9 synthesises sediment and transport parameters, while Table 10 provides an overview of all biogeochemical parameters used in OMEN-SED.
2.4.1 Transport parameters
The burial of sediments and pore water is directly related to the accumulation of new material on the sea floor (i.e. sedimentation, Burdige, 2006). This results in a downward advective flux of older sediment material and pore water in relation to the sediment–water interface. When coupled to an ocean model, its sedimentation flux can be readily used in OMEN-SED. The stand-alone version of OMEN-SED uses the empirical global relationship between the sediment accumulation rate (w in cm yr−1) and sea-floor depth (z in m) of Burwicz et al. (2011):
with parameter values as found in the original study (i.e. w1=0.117 cm yr−1, w2=0.006 cm yr−1, z1=200 m, z2=4000 m, c1=3, c2=10). As an option we include the parameterisation of Middelburg et al. (1997):
As mentioned before (Sect. 2.1), the diffusion coefficient of species i is calculated as for dissolved species and Di=Dbio for solid species. The bioturbation coefficient Dbio (cm2 yr−1) is constant in the bioturbated zone and also follows the empirical relationship by Middelburg et al. (1997):
Observations indicate that bioturbation is largely restricted to the upper 10 cm of the sediments and is only marginally related to sea-floor depth (e.g. Boudreau, 1998; Teal et al., 2010). Therefore, OMEN-SED imposes a globally invariant bioturbation depth zbio of 10 cm. In the case that the bottom water oxygen concentration is low (here < 4.5 nmol cm−3, which is often used to define suboxic waters; e.g. Morrison et al., 1999; Karstensen et al., 2008) infaunal activity is assumed to cease and zbio=0.01 cm. We choose a low value unequal to zero in order to simplify the implementation of the model. This approach ensures that the sediment column always consists of a bioturbated (even though very small for the low oxygen condition) and a non-bioturbated zone, and thus the same GBCM algorithm can be used to solve the conservation equations. Furthermore, when OMEN-SED is coupled to an Earth system model the same method can be used to convert the POC depositional flux into an SWI concentration (i.e. the flux needs to be converted assuming bioturbation; see Sect. 4.1).
Bio-irrigation (i.e. the pumping activity by burrow-dwelling animals) exchanges burrow water with overlying water and may enhance the SWI flux of solutes (Aller, 1984, 1988). Several approaches exist to incorporate this into a 1-D diagenetic model, for instance as a non-local transport–exchange process (Boudreau, 1984; Emerson et al., 1984) or as an enhancement factor of the molecular diffusion coefficient (Devol and Christensen, 1993; Soetaert et al., 1996). In OMEN-SED the latter approach is applied and the apparent “bio-diffusion” coefficient is calculated as . Soetaert et al. (1996) derived an empirical relationship between fir and sea-floor depth () based on observations from Archer and Devol (1992) and Devol and Christensen (1993), which is used in OMEN-SED. The specific molecular diffusion coefficients Dmol,i are corrected for sediment porosity ϕ and tortuosity F and are linearly interpolated for an ambient temperature T (in ∘C) using zero-degree coefficients and temperature-dependent diffusion coefficients (Soetaert et al., 1996):
Tortuosity can be expressed in terms of porosity as (Ullman and Aller, 1982) with the exponent m varying according to the type of sediment (here m=3 is used representing muddy sediments with high porosity). Values for and are summarised in Table 9 and are adapted from Li and Gregory (1974), Schulz (2006) and Gypens et al. (2008).
Middelburg et al. (1997)Boudreau (1998)Teal et al. (2010)Middelburg et al. (1997)Soetaert et al. (1996)(Li and Gregory, 1974; Schulz, 2006; Gypens et al., 2008)2.4.2 Stoichiometries and reaction parameters
The first-order organic matter degradation constants of compound class i, ki (yr−1), are assumed invariant along the sediment column and therefore independent of the nature of the terminal electron acceptor. The rate constants can be altered manually to fit observed sediment profiles (compare modelled profiles in Sect. 3.2) or related to a master variable provided by a coupled Earth system model (e.g. sedimentation rate; see Sect. 4.2). The partitioning of the bulk OM pool into reactivity classes (fi) needs to be specified manually in the stand-alone version or can be provided by the ESM. Organic matter degradation releases N, P and DIC to the pore water using Redfield molar ratios (Redfield, 1963) and consumes TEA with specific stoichiometries (O2C, NO3C, SO4C) as summarised in Table 10. Table A1 in the Appendix provides a list of reactions and their stoichiometries as implemented in OMEN-SED. The effect of OM degradation, secondary redox reactions and pyrite precipitation on total alkalinity is also accounted for via reaction-specific stoichiometries representing the release of NH4, H2S and P and is based on Jourabchi et al. (2005). In reality, the reoxidation of reduced substances produced during OM degradation may be incomplete. Yet, in OMEN-SED we have to assume their complete, instantaneous reoxidation at zox to allow for an analytical solution. In order to relax this assumption for cases in which it can be justified, we include a “switch” to allow part of the NH4, H2S and CH4 flux to escape reoxidation. The secondary redox parameters (i.e. , , ) therefore account for the fraction of reduced substances that are reoxidised and would ideally be parameterised, for instance, in relation to bottom water oxygen concentration or oxygen penetration depth (zox). Gypens et al. (2008), for example, expressed as a function of oxygen penetration depth () based on a fitting exercise to a numerical model and showed that the fraction varies between 0.2 for zox=0.1 cm and 1.0 for zox>3 cm. Due to mathematical constraints in OMEN-SED for finding an analytical solution to the model equations these fractions take constant values generally representing oxygenated deep sea conditions. However, when coupled to an ESM, becomes dependent on the bottom water oxygenation state. That is, for oxic bottom waters and a user-defined value for anoxic bottom waters. The parameter γFeS represents the fraction of sulfide that is precipitated as pyrite in the sulfidic zone. The majority of H2S produced by sulfate reduction is reoxidised, but it is estimated that ∼10–25 % is eventually buried as pyrite (Bottrell and Newton, 2006). However, this fraction can vary significantly over geological timescales (Berner, 1984). If a user does not want to make any assumptions about pyrite precipitation, it can be set to zero (as in the results presented here). The instantaneous equilibrium adsorption coefficients of NH4 and PO4 (, , ) are based on Wang and Van Cappellen (1996) and Slomp et al. (1998), respectively. The first-order rate constants for the sorption of PO4 to Fe oxides (ks), the release of PO4 from Fe-bound P due to Fe-oxide reduction (km) and authigenic CFA precipitation (ka), as well as the pore water equilibrium concentrations for P sorption and CFA precipitation (, ) and the asymptotic concentration for Fe-bound P (FeP∞) are taken from Slomp et al. (1996). See Table 10 for a complete summary of the parameters and their values.
(Wang and Van Cappellen, 1996; Slomp et al., 1998)(Slomp et al., 1996)3.1 Sensitivity analysis
3.1.1 Methodology
Model parameters implicitly account for processes that are not explicitly resolved. They are notoriously difficult to constrain and thus a primary source of uncertainty for numerical and analytical models, in particular on the global scale and/or in data-poor areas. A comprehensive sensitivity analysis can help quantify this uncertainty and identify the most sensitive parameters. More specifically, sensitivity analysis is used to investigate how the variations in the outputs () of a model can be attributed to variations in the different input parameters (; Pianosi et al., 2016). Different types of sensitivity indices, which quantify the relative influence of parameter xi on output yj with a scalar Si,j (for and ), can be calculated, ranging from simple one-at-a-time methods to statistical evaluations of the output distribution (e.g. variance-based or density-based approaches; Pianosi et al., 2016). The latter indices take values between zero and one (), where zero indicates a non-influential parameter and a higher value a more influential parameter. Here, sensitivity analysis is used mainly to identify which parameters have the largest impact on the different model outputs and therefore require more careful calibration. As the probability density functions of our model outputs (i.e. the resulting SWI fluxes) are generally highly skewed towards extreme organic matter degradation rates (not shown), variance-based sensitivity indices may not be a suitable proxy for output uncertainty (Pianosi et al., 2016). Hence, instead the density-based PAWN method by Pianosi and Wagener (2015) is employed which considers the entire conditional and unconditional cumulative distribution function (CDF) of the model output rather than its variance only. The unconditional CDF, Fy(y), of output y is obtained when all uncertain parameters () are varied simultaneously, and the conditional CDFs, , are obtained when all inputs but the ith parameter are varied (i.e. xi is fixed to a so-called conditioning value). The sensitivity index of parameter i is measured by the distance between the two CDFs using the Kolmogorov–Smirnov statistic (Kolmogorov, 1933; Smirnov, 1939), i.e.
Since accounts for what happens when the variability due to xi is removed, the distance between the two CDFs provides a measure of the effects of xi on the output y. Due to the model complexity it is impossible to compute the sensitivity indices analytically. Therefore, they are approximated from a Latin hypercube sampling of parameter inputs and calculated outputs. For a brief description of the methodology, see Fig. 4. For more details, we refer the interested reader to Pianosi and Wagener (2015).
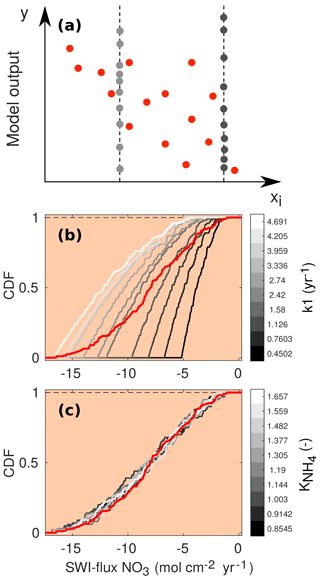
Figure 4(a) Schematic of the PAWN method, plotting an uncertain parameter (xi) against a generic model output (y). Red dots represent points for calculating the unconditional CDF (NU, here 15), and grey dots are points for calculating each conditional CDF (NC, here 10) with n=2 conditioning points as an example. The user can change the values of NU, NC and n. The number of model evaluations equals Neval= NU + n⋅ NC ⋅ M, where M is the number of uncertain input parameters. (b, c) Two examples of CDFs for the model-calculated SWI flux of NO3 using NU = 200, NC = 100 and n=10. The red lines are the unconditional distribution functions Fy(NO3) and the grey lines are the conditional distribution functions at different fixed values of the input parameters k1 (b) and (c). As the maximal distance between conditional CDFs and unconditional CDF is greater for k1, this parameter is more influential for the model output (here the SWI flux of NO3; compare to Fig. 5).
Table 11Range of model parameters used for the sensitivity analysis of model-predicted output.
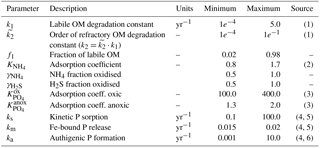
Sources: (1) Arndt et al. (2013); (2) Van Cappellen and Wang (1996); (3) Krom and Berner (1980); (4) Gypens et al. (2008); (5) Slomp et al. (1996); (6) Van Cappellen and Berner (1988).
The PAWN method, as implemented within the Sensitivity Analysis for Everyone (SAFE) MATLAB toolbox (Pianosi et al., 2015), is used to investigate M=11 model parameters for ranges as specified in Table 11. Sensitivity indices for all resulting SWI fluxes for two idealised sediment conditions (i.e. anoxic at 400 m and oxic at 4000 m; see Table 12) are calculated. We use NU = 200 samples to estimate the unconditional CDF, NC = 100 samples to estimate the conditional CDFs and n=10 conditioning points. Thus, as , 11 200 model evaluations are performed for each sediment condition. The resulting indices are then translated into a colour code and summarised in a pattern plot to simplify comparison (Fig. 5).
3.1.2 Results
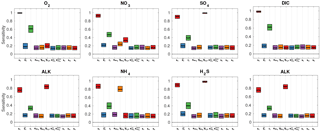
Figure 5 summarises the results of the sensitivity analysis as a colour map. Results indicate that generally the most significant parameters for all model outputs are the degradation rate constant for the labile OM pool (k1) and the fraction of this pool to the total OM stock (f1). Other parameters play a minor role for the SWI fluxes, with the exception of the secondary redox parameters (i.e. ) in the oxic scenario. Here, NH4, SO4 and H2S fluxes are very sensitive to changes in and , as these parameters determine how much of the respective TEA is produced in situ via reoxidation, thus affecting the resulting SWI fluxes. For the oxic scenario, the reoxidation of H2S produced in the sulfidic layer has also a strong influence on alkalinity (; Table 8, Eq. 5) as it decreases alkalinity by 2 moles per mole of S oxidised (; Table 10). However, these high sensitivities are partially caused by the wide range of allowed values (, ). Yet, for oxic deep sea conditions it is more likely that reduced substances are almost completely reoxidised (e.g. Hensen et al., 2006). For the anoxic scenario the secondary redox parameters are essentially non-influential as no O2 is available for the reoxidation of reduced substances. Especially for the oxic condition the PO4 SWI flux appears to be insensitive to P-related parameters (i.e. , , ks, km, ka) as the majority is absorbed to Fe oxides. The sensitivities change if other PO4-related equilibrium concentrations , and FeP∞ are used (not shown). Overall the results of the sensitivity analysis are in line with what one would expect from a diagenetic model and thus provide grounds to confirm that OMEN-SED provides sensible results. The parameterisation of the organic matter pools (f1) and their degradation rate constants (k1, k2) is critical, especially when the model is used in a global Earth system model framework, as these parameters, as well as the γ parameters, can have a very important influence on the flux of dissolved species through the SWI. At the same time these are the weakest constrained parameters. Thus, one should rather choose γ values close to 1 and consider carefully where a relaxation of the “all reoxidised” assumption is appropriate. In contrast, the importance of the OM degradation rate constants cannot be overemphasised. Therefore, much care should be given to how these are parameterised in coupled simulations and a range of different plausible scenarios should be tested to quantify uncertainty.

Figure 5Pattern plot showing the output sensitivity for each SWI flux (i.e. the chemical compounds on the vertical axis) and each input factor (i.e. the model parameters on the horizontal axis) for two idealised sediment cores. White patterns are assigned where the SWI flux is independent of the specific parameter.
Because of the strong sensitivity of model results to OM degradation rate parameters, we further explore the sensitivity of simulated sediment–water exchange fluxes to variations in organic matter degradation parameters by varying k1, f1 and while all other model parameters are set to their default values (Tables 9 and 10). Minimum and maximum values for k1, and f1 in the shallow ocean are as in Table 11. For the deep sea condition we account for the presence of more refractory OM by sampling , whereas the variation of k1 and is as in the shallow ocean. The parameter space is sampled using another Latin hypercube approach with sample sizes of N=3500 for each idealised sediment condition. Figure 6 summarises the results of the sensitivity study, and the ranges of observed O2 and NO3 sediment–water interface fluxes extracted from a global database (Stolpovsky et al., 2015) are indicated on the colour scale. The colour patterns in Fig. 6a and b reveal the complex interplay between the amount of labile OM f1 and its degradation rate k1 for the resulting SWI fluxes of NO3 in anoxic sediments and O2 in aerobic sediments. In general, a higher degradation rate in combination with more labile OM available leads to a higher SWI flux. However, higher fluxes extend over a larger range of k1 values when the amount of labile OM f1 is high. The absence of a colour pattern in Fig. 6c highlights the limited interaction of the two model parameters for NO3 SWI fluxes under oxic conditions. Figure 6 shows that SWI fluxes can vary widely over the range of plausible organic matter degradation parameters and that simulated fluxes generally fall within the range of observed SWI fluxes. However, a large number of different k−f combinations can result in SWI fluxes that fall within the observed ranges reported by Stolpovsky et al. (2015), further emphasising the care that should be devoted to constraining OM degradation parameters.
3.2 Case study: simulations of sediment cores
3.2.1 Methodology
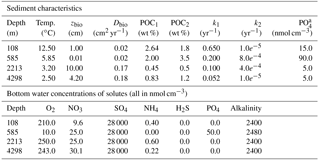
In order to illustrate the capabilities of OMEN-SED, comprehensive datasets from the Santa Barbara Basin (Reimers et al., 1996), the Iberian margin and the Nazaré Canyon (Epping et al., 2002) are modelled. Modelled profiles are compared with measured pore water data from different depths including the continental shelf (108 m) and the lower slope (2213 m) located at the Iberian margin, the upper slope (585 m) from the Santa Barbara Basin and a deep sea site (4298 m) in the Nazaré Canyon. The Santa Barbara Basin is characterised by anoxic bottom waters, high POC concentrations and varved sediments (Reimers et al., 1990), and therefore the depth of bioturbation in OMEN-SED is restricted to the upper 0.01 cm. In the uppermost sediments iron(III) hydroxides are reduced, releasing Fe2+, which reacts with sulfide to form iron sulfides. Thus, the Fe cycle exerts a strong control on sulfide concentrations in the sediments of this basin (Reimers et al., 1996). In addition, the sediments are generally supersaturated with respect to carbonate fluorapatite by and below 2 cm (Reimers et al., 1996). The Iberian margin, situated in the north-eastern Atlantic, generally belongs to the more productive regions of the global ocean (Longhurst et al., 1995); however, seasonal changes in upwelling creates a strong temporal variability in primary productivity and organic carbon deposition. Submarine canyons in this area (like the Nazaré Canyon) may deliver organic carbon from the shelf to the ocean interior (van Weering et al., 2002; Epping et al., 2002). For a more detailed description of the study areas and the experimental work, the interested reader is referred to the publications by Reimers et al. (1996) and Epping et al. (2002).
In OMEN-SED sediment characteristics and boundary conditions are set to the observed values where available (Table 13). Other sediment characteristics (e.g. sedimentation rate, porosity, density), stoichiometric factors and secondary reaction parameters are set to the default value (see Tables 9 and 10). Organic matter is modelled as two fractions with different first-order degradation rate constants. The POC and pore water profiles were manually fitted by optimising the POC partitioning into the fast- and slow-degrading pool and their respective first-order degradation rate constants (priority is given to reproducing the POC and O2 profiles). For phosphorus the equilibrium concentration for authigenic P formation () was adjusted to fit the PO4 concentration at zmax.
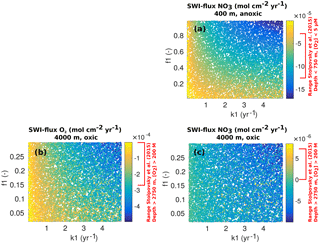
Figure 6Scatter plots (k1 vs f1) of resulting OMEN-SED SWI fluxes for the 400 m anoxic (a: NO3) and 4000 m oxic (b: O2, c: NO3) scenario. Negative values represent a flux from the water column into the sediments. Ranges indicated in red on the colour scale correspond to observed benthic fluxes as reported in the global database of Stolpovsky et al. (2015).
Table 13Boundary conditions for simulated sediment profiles at the Iberian margin (108 and 2213 m), the Santa Barbara Basin (585 m) and the Nazaré Canyon (4298 m) reported in Fig. 7. For all sites a DIC bottom water concentration of 2400 nmols cm−3 is assumed.
3.2.2 Results
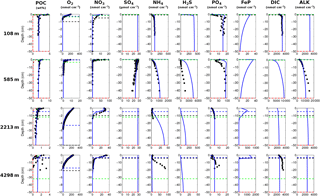
Figure 7Modelled (curves) and measured (filled dots) solid-phase and dissolved pore water profiles for four different sediment cores. Note that different scales are used for different stations. The blue POC curve represents the sum of the refractory (green) and labile (red) POC fraction. The horizontal dashed lines in each panel indicate the bioturbation depth (black) and the penetration depths of oxygen (blue), nitrate (green) and sulfate (red) as calculated by OMEN-SED.
Figure 7 compares modelled and observed sediment profiles for the Santa Barbara Basin and the Iberian margin. Results show that OMEN-SED is able to capture the main diagenetic features across a range of different environments without changing model parameters (other than the four we tuned, i.e. k1, k2, f1 and ) to site-specific conditions. For the two open Iberian margin stations (108 and 2213 m) OMEN-SED fits all observations well. OMEN-SED does especially well at a sea-floor depth (SFD) of 2213 m by reproducing the deep O2 penetration and the subsurface maximum in NO3 concentration due to the nitrification of NH4 (note that NH4 is overestimated at this SFD). For the anoxic Santa Barbara Basin (585 m) the decrease in SO4 and the increase in ALK concentration with sediment depth is well represented, indicating the importance of sulfate reduction as the primary pathway of OM degradation at this site (compare with Meysman et al., 2003). However, a misfit is observed for H2S and PO4 in the upper 20 cm of this sediment core. The discrepancy for H2S can be explained by high iron(III) hydroxide concentrations, which is reduced to degrade organic matter (especially in the 2–4 cm depth interval), therefore placing the beginning of the sulfate reduction zone and the production of H2S in the deeper sediments (Reimers et al., 1996). Iron processes are currently not dynamically represented in OMEN-SED. In addition, produced dissolved Fe reacts with H2S to form iron sulfides (e.g. pyrite, FeS2) and thus further inhibits the rise of H2S (Reimers et al., 1990). The iron cycle also plays a critical role for phosphorus, as the reduction of iron(III) hydroxides in the surface sediments releases sorbed phosphate, leading to pore waters around and below 2 cm which are supersaturated with respect to fluorapatite, thus initiating CFA precipitation. Reimers et al. (1996) could even show that the accumulation of CFA is mainly restricted to the near-surface sediments (∼5 cm) instead of throughout the sediment column. As OMEN-SED currently does not include an iron cycle and Fe-bound P and CFA processes are highly parameterised, the model is not able to capture these complex, non-steady-state phosphorus dynamics at this specific site. For the Nazaré Canyon station (4298 m) satisfactory fits could be realised apart from NH4. However, Epping et al. (2002) also could not obtain a better fit using the diagenetic model OMEXDIA. They suggested non-local solute exchange resulting from bio-irrigation as responsible for the higher NH4 concentrations at this site, which is neglected in their model and in OMEN-SED. Furthermore, the fractured POC profile (indicating episodic depositional events through the canyon) could have been approximated using a different partitioning of the bulk POC into the labile and refractory pool with different degradation rate constants, thus potentially leading to a better fit of the NH4 profile. In general, better approximations of the data could have potentially been acquired by applying a sensitivity study using different NC ratios (e.g. Epping et al., 2002, report different ratios from Redfield stoichiometry) and exploring the parameter space for the secondary reaction parameters (, ). However, considering these generalisations and our assumption of steady state, which might not be valid, particularly for the complex Santa Barbara Basin, the shallow core and the Nazaré Canyon, which are affected by seasonality and biology, OMEN-SED generally reproduces the observed pore water trends and hence captures the main diagenetic processes.
Table 14Sea-floor depth dependency of key model parameters and boundary conditions (adapted from Thullner et al., 2009).
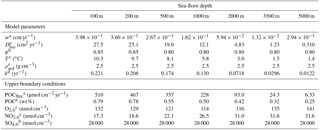
a Derived from Middelburg et al. (1997).b Derived from Van Cappellen and Wang (1995).
c Derived from Conkright et al. (2002). d Derived from
Boudreau (1997).
e Calculated with OMEN-SED from POCflux.
3.3 Case study: stand-alone simulations of global ocean transect
3.3.1 Methodology
In this section we explore to what degree OMEN-SED is capable of capturing the dynamics of organic matter degradation pathways and related TEA fluxes as simulated with a more complete and complex numerical diagenetic model (Thullner et al., 2009). Therefore, we reproduce the simulations of typical conditions along a global ocean hypsometry of Thullner et al. (2009) and compare our modelled TEA fluxes with the results of the complex model and with observations from Middelburg et al. (1996). To explore the global degradation of OM in the sea floor, Thullner et al. (2009) quantified various diagenetic processes using the Biogeochemical Reaction Network Simulator (BRNS; Aguilera et al., 2005), a flexible simulation environment suitable for reactive transport simulations of complex biogeochemical problems (e.g. Jourabchi et al., 2005; Thullner et al., 2005). Thullner et al. (2009) used sea-floor depth (SFD) as the master variable and calculated model parameters, such as w, Dbio and ϕ, from existing empirical relationships (e.g. Van Cappellen and Wang, 1995; Middelburg et al., 1997). Organic matter degradation was described with a 1G approach, thus assuming a single pool of organic matter of uniform reactivity. The first-order rate constant was related to the sediment accumulation rate, w (cm yr−1), following the empirical relationship of Boudreau (1997):
This rate constant can be assumed as the mean reactivity of the organic matter fractions which are degraded in the upper, bioturbated 10–20 cm of the sediments. Thus, more reactive fractions (degraded during days or weeks close to the SWI) and more refractory fractions (degraded on longer timescales deeper in the sediments) are not captured by this relationship (Boudreau, 1997). BRNS simulations were performed using boundary conditions and parameters for depths representative of shelf, slope and deep sea sediments (i.e. SFD of 100, 200, 500, 1000, 2000, 3500 and 5000 m). In order to reproduce these results, OMEN-SED is configured here as a 1G model and boundary conditions and model parameters are defined as in Thullner et al. (2009, see Table 14). As OMEN-SED assumes a fixed fraction (i.e. , ) of reduced substances to be reoxidised, which exerts a large impact on the resulting SWI fluxes (compare to Sect. 3.1), two sets of simulations are performed in order to show the range of possible model outputs. In the first set-up 95 % of the reduced substances are reoxidised (i.e. ), and in the second less realistic case, only 5 % are reoxidised (all other model parameters and boundary conditions are equal).
3.3.2 Results
Figure 8 compares simulated SWI fluxes of TEAs (i.e. O2, NO3 and SO4) along the global hypsometry using OMEN-SED (black lines) with the results of Thullner et al. (2009) (red lines). Observations for O2 and NO3 fluxes are taken from Middelburg et al. (1996). Due to the applied empirical relations, organic matter flux to the sea floor decreases by 2 orders of magnitude from 100 to 5000 m and its degradation rate constant by 1 order of magnitude (Table 14). Therefore, the rate of organic matter degradation is about 50 times greater at 100 m than at 5000 m (compare to Thullner et al., 2009), thus resulting in a decrease in TEA fluxes along the hypsometry (Fig. 8). The 95 % reoxidation experiments (dots) show proportionally higher O2 influxes than the 5 % reoxidation experiments (triangles) because more O2 is utilised for the in situ production of NO3 and SO4 in the sediments. This is also mirrored by the increased NO3 outflux and decreased SO4 influx for shallower SFDs. This is in line with the results of Thullner et al. (2009), which showed that in situ production is an important pathway of SO4 supply in the sediment responsible for ∼ 80 % of the total OM degradation at depths between 100 and 2000 m (in our results SO4 is not used for OM degradation in OMEN-SED below 2000 m). In general, Fig. 8 shows that OMEN-SED captures the main trends in observed and numerically simulated TEA fluxes well. Results also confirm that higher γ values better represent SWI fluxes for most of the global hypsometry. A slight overestimation of shallow ocean SWI fluxes (SFD < 200 m) for the high γ scenario indicates that slightly lower γ values would better capture SWI fluxes in these areas where rapid oxygen consumption favours the escape of reduced species across the SWI.
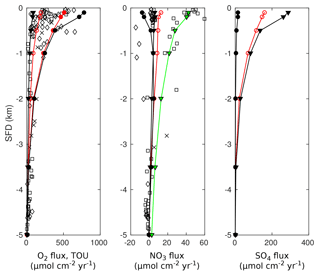
Figure 8Fluxes of O2, NO3 and SO4 to the sediment along the global hypsometry. Red lines (with open symbols) are modelled fluxes from Thullner et al. (2009) using BRNS; black lines are results from OMEN-SED (• : ; ▾: ). Observations of TEA fluxes are taken from Middelburg et al. (1996) (◇: Atlantic, □: Pacific, ×: Arctic–Indian Ocean). Also plotted in the figure (far left panel) are the total oxygen uptake (TOU) estimates of Thullner et al. (2009) (filled red symbols). The green line indicates OMEN-SED results for low oxygen and high nitrate levels and the lower NC ratio. Positive fluxes are directed from the ocean into the sediments.
In addition, observed O2 fluxes in the upper 2000 m are generally encompassed by our total range in predicted OMEN-SED fluxes. Oxygen fluxes for the deep sea sediments, however, are slightly underestimated. These deviations can presumably be related to the assumed 1G description of organic matter degradation, which neglects the more labile OM pool. This highly reactive pool is degraded close to the sediment surface, thus promoting higher aerobic degradation rates and higher O2 fluxes. Nitrate fluxes in the upper 500 m of the Atlantic Ocean are well predicted. However, as in Middelburg et al. (1996) the direction of calculated nitrate fluxes in the upper 1000 m of the Pacific Ocean differ from the observations. Middelburg et al. (1996) related these discrepancies to the globally averaged model parameters and the applied boundary conditions. They could reduce the disagreements significantly by using more representative bottom water concentrations for the eastern Pacific and a higher flux of labile organic matter for their 2G model. By changing the boundary conditions and the N : C elemental ratio of organic matter for the whole hypsometry, it is possible to obtain a better model–data fit with OMEN-SED for the shallow Pacific Ocean (green line in Fig. 8b). Bohlen et al. (2012) report that the elemental N : C ratio strongly deviates from Redfield stoichiometry (0.151) with specifically lower values for the eastern Pacific Ocean. The use of their globally averaged value of 0.067 allows the modelled and observed values to be reconciled provided that bottom water conditions are also changed to the low oxygen and high nitrate levels more likely to be found in the shallow Pacific Ocean (O2=10 nmol cm−3 and NO3=80 nmol cm−3).
4.1 Coupling to the cGENIE Earth system model
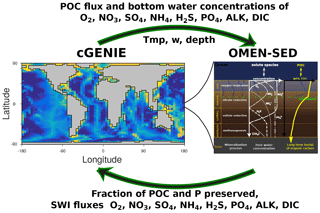
Figure 9Schematic of the relationship between OMEN-SED and cGENIE. Arrows represent the information transferred between models.
In a final step, we couple OMEN-SED to the carbon-centric version of the GENIE Earth system model (cGENIE; Ridgwell et al., 2007) in order to illustrate how a fully coupled ocean–sediment system can be configured and applied. We start by providing a brief description of cGENIE and the coupling procedure (Fig. 9).
cGENIE is a model of intermediate complexity based on the efficient climate model C-GOLDSTEIN of Edwards and Marsh (2005), featuring a frictional-geostrophic 3-D ocean circulation model coupled to a fast energy–moisture balance 2-D atmosphere together with a dynamic–thermodynamic sea-ice component. The version of cGENIE used here includes the marine geochemical cycling of carbon, oxygen, phosphorus and sulfur (Ridgwell et al., 2007), the preservation of carbonates in deep sea sediments (SEDGEM; Ridgwell and Hargreaves, 2007) and terrestrial weathering (Colbourn et al., 2013). The ocean model is implemented on a 36 × 36 equal-area horizontal grid with 16 vertical levels using the pre-industrial continental configuration and bathymetry as in Archer et al. (2009). A finer grid (72 × 72) is used for the sediments (see Fig. 11c and Ridgwell and Hargreaves, 2007) and OMEN-SED is called by SEDGEM for each wet ocean grid point.
In our Earth system model set-up, we prescribe the burial sediment fluxes of detrital material, opal and CaCO3, while leaving OMEN-SED to calculate organic matter preservation. This assumption serves two purposes. First, the runtime of the model is minimised as steady-state conditions are reached earlier compared to the ca. 20–50 kyr adjustment time for surface sediment CaCO3 (Ridgwell and Hargreaves, 2007). Second, invariant flux fields remove feedbacks between OMEN-SED and the calculation of CaCO3 preservation (changes in organic matter preservation affect CaCO3 dissolution and hence sedimentation accumulation rates, which in turn affects the weight percent of organic matter in the sediments) that would not only lengthen the sediment adjustment time but also make it impossible to carry out unbiased comparisons between different assumptions regarding organic matter reactivity in OMEN-SED.
We derive these fields form the data compilation of Archer (1996) as follows. First, we re-grid the Archer (1996) interpolated non-carbonate mass accumulation rate field (NCflux) to the 72 × 72 cGENIE sediment grid. This field includes detrital material plus opal (plus a minor contribution from organic matter). We could then directly calculate ∑flux (total burial flux of all components or total sediment accumulation rate) from this plus measurements of coretop wt % CaCO3 (Cwtpct) (Archer, 1996) as . However, some of the Archer (1996) database Cwtpct values are both close to 100 % and associated with high NCflux and hence would lead to unrealistically high values for ∑flux. We therefore impose a plausibility filter by also re-gridding coretop wt % opal (Owtpct) and quartz (Qwtpct) and for grid points in which more than one component is reported and the sum exceeds 100 wt %, normalising the individual components (for grid points with only a single solid component, no change is made). We then calculate the individual solid component burial fluxes, and sum them up. To interpolate between the grid points associated with data, we iteratively average nearest (adjoining) neighbours. The distribution of the total burial flux ∑flux (in g cm−2 kyr−1) is shown in Fig. C1 in the Appendix.
Depending on the configuration of the overlying biogeochemical ocean model, processes can be included or excluded in OMEN-SED and stoichiometric factors (Table 10) need to be matched between models to ensure preservation of mass. As nitrogen is not modelled explicitly in the employed cGENIE configuration, NCi, ALKNIT and ALKDEN in OMEN-SED are set to zero. cGENIE, however, implicitly includes the effects of NH4 release and its complete nitrification on alkalinity but neglects the impact of P release. Therefore, alkalinity stoichiometries for aerobic degradation, sulfate reduction and methanogenesis are changed to , and , respectively (compare to default in Table 10).
Various biogeochemical tracers and parameters are transferred from SEDGEM to OMEN-SED (see Fig. 9) and are converted into the required units. Bottom water concentrations of solutes are converted from mol kg−1 to mol cm−3 and the depositional flux of POC (POCflux) is converted from cm3 cm−2 yr−1 to mol cm−2 yr−1 assuming an average density of POC of 1.0 g cm−3. Within the water column in cGENIE, POC is partitioned into two fractions with different degradation length scales of ∼ 590 m and 1 000 000 m. The labile pool thus degrades while sinking through the water column, whereas the refractory pool is assumed relatively unreactive (Ridgwell et al., 2007). Thus, depending on sea-floor depth, the partitioning of bulk POC reaching the sediments is different (Fig. 10a, b). This information is used by OMEN-SED to define the parameter f1. Other parameters used from cGENIE are sea-floor depth and local temperature. The sediment accumulation rate (w) is taken from the previous time step of cGENIE; however, it is assured that w is not smaller than the detrital flux (Detflux) to the sediments (e.g. w<0 can occur if initially carbonate-rich sediments are eroded during the spin-up of cGENIE). In the case (w≤Detflux & Detflux=0.0), all POC is remineralised at the ocean floor. Furthermore, a minimum value of w=0.4 cm kyr−1 is imposed as OMEN-SED tends to be less stable for lower values. For comparison, this threshold is crossed for sea-floor depths below 7000 m when applying the relationship between the sediment accumulation rate and water depth of Middelburg et al. (1997) and below 5200 m for the Burwicz et al. (2011) parameterisation. The bulk POCflux is separated into the labile and refractory component and the routine to find the steady-state solution for POC is called. Here, the two POC depositional fluxes are first converted into SWI concentrations (POCi(z=0), in mol cm−3) by solving the flux divergence equation
for z=0. OMEN-SED then computes the fraction of POC preserved in the sediment (fPOC, see Eq. 5) and subsequently calls the routines to find the steady-state solutions for the solute substances. Note that in this initial coupling the calculated benthic uptake and return fluxes of dissolved species Ci (compare to Eq. 6) are adjusted for the advective loss at the lower sediment boundary (w⋅Ci(zmax)) to ensure the conservation of mass in the coupled model:
In the case that OMEN-SED computes unrealistic results for POC preservation (i.e. fPOC<0.0 or fPOC>1.0) we discard the results of OMEN-SED and all POC is remineralised at the ocean floor. For the modern ocean set-up using the adjustments for w described above, this has not occurred and is just installed as a safety check. Finally, fPOC and the SWI fluxes of solutes (, in mol cm−2 yr−1) are returned to cGENIE. In the case that no POC is deposited on the sea floor (i.e. POCflux=0), OMEN-SED is not executed and fPOC and for all i are set to zero. In order to reduce memory requirements, the sediment profiles (e.g. as shown in Fig. 7) are not calculated in the FORTRAN version of OMEN-SED; however, the boundary conditions are saved and sediment profiles for specific grid cells, ocean basins and ocean transects can be plotted at the end of each experiment using the stand-alone MATLAB version of OMEN-SED.
4.2 Parameterising the OM degradation rate constants in a global model
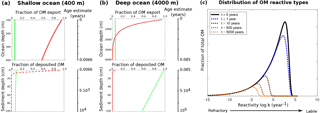
Figure 10Idealised relationship of organic matter decomposition during remineralisation in the water column and the sediments. (a, b) Upper panels: water column development of the two organic matter fractions as represented in cGENIE for two ocean depths (red: labile OM with degradation length scale of 589 m; green: refractory OM, which is unreactive in the water column). The values are normalised to OM export at 100 m. Age estimates for the OM since its export from the euphotic zone are calculated using a sinking velocity of 125 m day−1. (a, b) Lower panels: schematic representation of the development of the two OM fractions in the sediments (normalised to OM deposited on the sea floor). For the age estimates in the sediment column a sediment accumulation rate of 0.01 and 0.001 cm yr−1 is assumed. (c) Idealised distribution functions of OM reactive types during remineralisation for different OM ages assuming a reactive continuum model for OM degradation. The initial distribution (at t=0) represents fresh OM when it is exported from the euphotic zone (characterised by yr−1 and ν=0.125; Boudreau et al., 2008).
As shown in our sensitivity analysis (Sect. 3.1) and discussed by Arndt et al. (2013), the degradation rate constants for OM (ki) are the most influential parameters and exert a dominant control on the SWI flux of redox-sensitive elements and the preservation of organic matter. Yet, their spatial variability is unknown at the global scale and reported rate constants in the sediments can vary by about 10 orders of magnitude or more (Middelburg et al., 1993; Arndt et al., 2013). Furthermore, when OMEN-SED is coupled to cGENIE, very different timescales have to be considered for OM degradation in the sediments compared to the water column (Fig. 10a, b), and thus the diagenetic rate constants cannot be easily implied by the assumed water column POC flux profiles in cGENIE. To illustrate this, let us consider the degradation of fresh marine organic matter as it is transported and degraded along the ocean–sediment continuum. The bulk material is composed of a complex mixture of different organic carbon compounds that can be described by a reactivity continuum. Microbes preferentially degrade the more reactive organic matter compounds first (Emerson and Hedges, 1988; Wakeham et al., 1997; Lee et al., 2000), resulting in the preferential preservation of more unreactive compounds and rendering the remaining mixture less and less reactive with time. Thus, depending on the age of OM (or depth in the water and sediment column) the reactivity distribution of its compounds changes significantly (Fig. 10c) and the multi-G (2G in this case) approximation of this continuum has to take this shift into account. Figure 10 illustrates these changes in the original reactivity distribution within an ocean–sediment framework. The reactivity distribution t<1 year represents the organic matter mixture after it settled through the water column (Fig. 10c). Only the most reactive OM compounds are remineralised. This explains why the POC flux in the ocean can be represented with a 1G or pseudo 2G degradation model. In the sediments, however, much longer timescales have to be considered and a wider range of more unreactive compounds are degraded. As a consequence, significant changes in the reactivity distribution already take place in the upper millimetres of the sediments (t∼10 years; Fig. 10c). Therefore, a broader range of OM reactive types must be represented by the degradation model to capture the reactivity spectrum of OM in surface sediments, explaining why at least a pseudo 3G model (including two degradable and one refractory fraction; Soetaert et al., 1996; Boudreau, 1997; Stolpovsky et al., 2015) is required. To complicate the situation even further, different sediment depths can represent very different timescales. For instance, half a metre of sediment can be deposited within a year in a coastal setting, while it will represent thousands of years (if not more) of sedimentation in a deep ocean setting. Therefore, residence times and thus degradation rate timescales (or OM age) are mainly controlled by sediment accumulation rates. For instance, assuming a sediment accumulation rate of 0.01 cm yr−1 for the shallow ocean, OM at 5 cm of depth has been degraded for approximately 500 years, whereas a deep ocean sediment accumulation rate of 0.001 cm yr−1 allowed for OM degradation of approximately 5000 years at the same depth. As a consequence, organic matter degradation in deep ocean sediments affects a much wider range of the reactivity continuum and our simple pseudo 3G approximation of the complex OM mixture needs to reflect this by allowing for different k and f values (Fig. 10c). Furthermore, by assuming steady state in OMEN-SED we assume that deposition fluxes of OM are constant over the characteristic timescales of the reaction–transport processes.
Thus, defining appropriate OM degradation rate constants is a major challenge and source of uncertainty for diagenetic models. The rate constants in models are either determined through profile fitting for a specific site or, for global applications, they are related to a single readily available characteristic (or master variable) of the local environmental conditions. For instance, considerable effort has been expended to relate the apparent rate constant for oxic and anoxic OM degradation to sedimentation rate (w) and various empirical relations have been proposed (Toth and Lerman, 1977; Tromp et al., 1995; Boudreau, 1997). Stolpovsky et al. (2015, 2018) suggested empirically derived approaches to constrain degradation rate constants in a 2G model on a global scale. These approaches are derived from present-day observations and might help constrain parameters for present-day applications. However, the problem of constraining 2G degradation model parameters remains for largely different environmental conditions encountered in the past that could also prevail in the future (Arndt et al., 2013). We hence test several alternative schemes in the coupled OMEN–cGENIE framework. Our objective is not to perform and discuss a detailed calibration of the coupled models as this is beyond the scope of this sediment model development paper. Rather, we want to showcase the feasibility of the model coupling, illustrate the range of results and thus the information that can be generated with OMEN-SED, and verify that the model results capture the main observed global benthic biogeochemical features.
4.2.1 Methodology
In this section we compare modelled mean POC weight percentages (wt %) in the upper 5 cm of the sediments (POC5 cm) to the global distribution pattern of POC content in surface sediments (< 5 cm sediment depth) of Seiter et al. (2004) using different parameterisations for the degradation rate constants k1 and k2. For our observational target we take the original POC distribution pattern in grid resolution (interpolated from > 5500 measurements; compare to Seiter et al., 2004) and transform it onto the 72×72 SEDGEM grid (Fig. 11). The re-gridding of the original POC distribution obviously affects the resolution of the data, especially for the continental margin, as some sites with higher POC wt % are lost in the re-gridding process (compare e.g. maximum values for the eastern Pacific and upwelling waters of the Namibian shelf; Fig. 11a, b). The colour of the points in Figs. 12–13 indicates the sea-floor depth (SFD) of the respective cGENIE grid cell. As the individual data points are highly scattered and in order to see if a certain relation between k1 and k2 performs better for specific ocean depths, the data points are binned into six uniform depth classes of 1000 m each (respective mean POC wt % and SFD are represented by the triangles). The regression line is calculated for the six bin classes and included in the figures.
Figure 11Observed distribution of sediment surface (< 5 cm) POC wt % (a, b) and cGENIE bathymetry (c). (a) Original global distribution of POC wt % interpolated on a grid from more than 5500 individual data points (compare to Seiter et al., 2004, for the interpolation procedure). (b) Observed POC wt % data transformed onto the 72×72 SEDGEM grid. Grid points without any observations are left blank (grey). (c) Gridded continental configuration and ocean bathymetry of the 16-level, 72×72 equal-area cGENIE grid.
To parameterise the reactivity of organic matter in OMEN-SED two different schemes are tested and compared. First, spatially uniform degradation rate constants k1 and k2 are assumed. By simulating two different pools of POC in the water column characterised by different degradation length scales (Ridgwell et al., 2007), cGENIE implicitly accounts for the decrease in mean POC reactivity with water depth. The rate constants for the more refractory OM pool, k2, are systematically varied and the more labile OM component, described by k1, is assumed to degrade multiple times faster. Values for these parameters are selected in accordance with the best fit to the global surface POC observations (Seiter et al., 2004). Although accounting for the decrease in mean POC reactivity with sea-floor depth, this approach does not take into account the change in the distribution of organic matter reactivity types caused by different sediment accumulation rates and thus different residence timescales in the sediments (Fig. 10). Therefore, the second approach uses the empirical relationship proposed by Boudreau (1997), which relates the apparent OM degradation rate constant in the upper sediments to the sediment accumulation rate, w (cm yr−1; see also Sect. 3.3):
Following Boudreau (1997) and Stolpovsky et al. (2015) it can be assumed that kapp represents the mean OM reactivity within the upper 10–20 cm of the sediments. The following assumptions are made in order to calculate the two degradation rate constants for OMEN-SED:
where x describes the relation between k1 and k2 and is subject to sensitivity experiments (with values of 20,25}). Note that the difference between k1 and k2 using this approach is significantly larger as in the globally uniform approach. As the fractions of labile and refractory OM reaching the sediments f1 is known from cGENIE, k1 and k2 can be calculated independently for each grid cell.
To simulate steady-state sediment composition we configure the model as a “closed” system, i.e. one in which there is no loss of CaCO3 through burial. The redox-dependent P cycle in OMEN-SED is not used in these experiments and all organic phosphorus is returned at the sea floor. To speed up the calculation and to ensure that ocean redox changes caused by OMEN-SED do not impact the sediment composition of CaCO3, we use the prescribed solid fields as described earlier. Apart from the prescribed fields and the 72×72 sediment grid the model is configured as in Archer et al. (2009) and atmospheric CO2 is restored to a pre-industrial value of 278 ppmv. First a 20 000 year spin-up is performed without OMEN-SED being coupled. All presented coupled cGENIE–OMEN simulations are run for 10 000 years to steady state from this spin-up. OMEN-SED is called for each grid cell in every time step, feeding back the resulting SWI fluxes and the fraction of POC preserved in the sediments to cGENIE.
4.2.2 Results
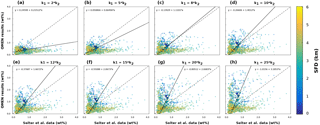
Figure 12Cross plots comparing modelled and observed mean POC wt % in the upper 5 cm of the sediments using the relationship of Boudreau (1997) and the assumptions of Eqs. (54) and (55) to calculate k1 and k2. Data points are binned into six uniform depth classes of 1000 m, and each class is represented by a triangle. Grid points with more than 4.0 POC wt % are not shown.
Figure 12 presents results for the relationship of Boudreau (1997) using the assumptions of Eqs. (54) and (55) to calculate k1 and k2. Here, the relation between the two degradation rate constants (Eq. 55) is changed globally and thus independent of the sea-floor depth. The cross plots show that it is not possible to achieve a solution in which all bin classes fall onto or close to the 1:1 line. Also, the slope of the regression lines is generally much larger or smaller than 1.0 (with the exception of Fig. 12c), indicating that the relationship between depth and observed POC wt % by bin class is not adequately represented by the model. When looking at the individual bin classes it can be seen that shallow ocean depths are better represented by smaller differences between k1 and k2 (e.g. for SFD < 1000 m; Fig. 12b) and the deep ocean by a larger spread (e.g. for SFD > 3000 m; Fig. 12h). These results reflect the preferential degradation of more reactive organic matter types (Wakeham et al., 1997; Lee et al., 2000) and thus the change in the distribution functions of OM reactive types for different OM ages (Fig. 10c). In the shallow ocean bulk POC consists of fresher organic matter types on average and is therefore generally more reactive overall (i.e. higher kapp due to higher w in the model) as in the deep ocean. In addition, OM at 5 cm of sediment depth in the deep ocean is generally older than in the shallow ocean due to lower sediment accumulation rates, and therefore more reactive types are affected by degradation and a larger spread between k values is needed to capture these dynamics (compare to Fig. 10c).
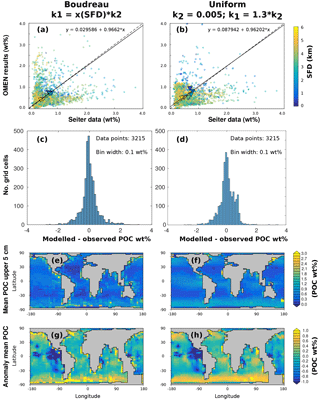
Figure 13Mean POC concentrations in the upper 5 cm of the sediments (POC5 cm) using the depth-dependent parameterisation adapted from Boudreau (1997, left) and the globally uniform model (k2=0.005, ; right). (a, b) Cross plots as shown in Fig. 12. (c, d) Histograms of the residuals of modelled minus observed POC5 cm. (e, f) POC5 cm as calculated with OMEN-SED. (g, h) Difference map of POC5 cm as calculated with OMEN-SED and interpolated data from Seiter et al. (2004).
Departing from our theoretical considerations (see discussion of Fig. 10c), we use these observations to create a depth-dependent relationship between the two degradation rate constants, where x in Eq. (55) is a function of SFD and takes values of x=5 for SFD < 1000 m, x=8 for 1000 m ≤ SFD < 2000 m, x=12 for 2000 m ≤ SFD < 3000 m and x=25 for SFD ≥ 3000 m for the six SFD bin classes, respectively. Figure 13 compares this depth-dependent approach with the best model using spatially uniform degradation rate constants (k2=0.005, ). In the depth-dependent approach all bin classes are close to the 1:1 line and the slope of the regression line (0.9662) indicates that the relationship between depth and observed POC wt % for the bin classes is well represented by the model (Fig. 13a). Using spatially uniform degradation rate constants, five of the six bin classes are located close to the 1:1 line (Fig. 13b), indicating that the simpler parameterisation also adequately captures the relationship between depth and observed POC wt % by bin class. The reason for this is that BIOGEM provides a depth-dependent POC flux and partitioning between the two fractions (Fig. 10). The shallowest bin class (between 0 and 1000 m) represents an exception, as OMEN-SED tends to overestimate POC preservation for this depth class. However, this could also be related to the re-gridding of the original POC distribution pattern of Seiter et al. (2004) onto the SEDGEM grid, as some data grid cells with higher POC wt % on the continental margin are lost due to the restricted SEDGEM resolution (compare to Sect. 4.2). The histograms (Fig. 13c, d) visualise the difference between modelled and observed mean POC concentrations and demonstrate the high density of data points close to the 1:1 line. For the depth-dependent approach, 92.5 % of the cGENIE grid cells show a difference between modelled and observed POC concentration of less than 1.0 POC wt %; in 79.9 % of the grid cells, the difference is less than 0.5 POC wt % (for the globally uniform approach the percentages are 95.37 and 70.95 %).
Both experiments reproduce minimal POC concentrations in the subtropical gyres and generally higher concentrations along the continental margins (Fig. 13e, f). Both experiments, however, underestimate mean POC wt % in the surface sediments of the equatorial eastern Pacific and overestimate POC concentrations in the North Pacific and Southern Ocean (Fig. 13g, h). The depth-dependent approach of Boudreau (1997) shows more spatial variability in POC preservation than the other parameterisation. In general, implementing lower anaerobic degradation rate constants when bottom water oxygen concentrations fall below a threshold value could potentially improve the simulation of higher POC concentrations in areas with high POC input to the sediments (Palastanga et al., 2011).
4.3 Modelled fluxes and sediment characteristics
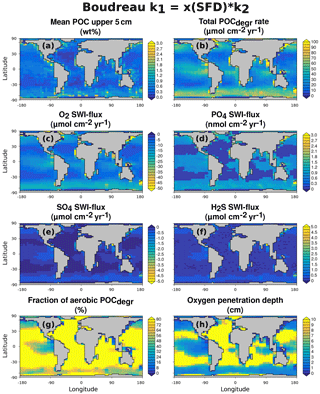
For the depth-dependent Boudreau (1997) approach modelled SWI fluxes and sediment characteristics are shown in Fig. 14. Modelled total POC degradation (POCdegr) rates in the upper sediments decrease from the shelves to the deep sea by up to 2 orders of magnitude (Fig. 14b). This is in agreement with data from the literature (e.g. Middelburg et al., 1993, 1997; Burdige, 2007) and other model results (e.g. Thullner et al., 2009) which indicate that the highest degradation rates in marine sediments are found in the coastal ocean (SFD < 200 m). Oxygen fluxes into the sediments (Fig. 14c) range from 0.0 for the deep ocean and sites without OM deposition to values of about 300 µmol cm−2 yr−1 for the shallow ocean with the highest POC degradation rates. Influx of SO4 into the sediments is rather low (between 0.0 and 23.9 µmol cm−2 yr−1) because in OMEN-SED 95 % of produced H2S is reoxidised to SO4, and therefore sulfate reduction is mainly driven by in situ sulfide oxidation. However, in general the coupled model fluxes fall well within the ranges predicted by the stand-alone global hypsometry experiments (O2 between 0.0 and 800 µmol cm−2 yr−1 and SO4 between 0.0 and about 300 µmol cm−2 yr−1; compare to Sect. 3.3). In accordance with the total POC degradation rates the release of PO4 shows a maximum value of 8.12 nmol cm−2 yr−1 on the shelves (Fig. 14d). The relative contribution of aerobic POC degradation in the upper sediments increases from the shelves to the deep sea (Fig. 14g), which is also consistent with estimates from Thullner et al. (2009) who found that oxygen is responsible for less than 10 % of POCdegr at 100 m SFD and for more than 80 % in the deep sea. The oxygen penetration depth in OMEN-SED increases from values below 1 cm at the shelves to more than 10 cm in the deep ocean (Figs. 14h and 15). Small oxygen penetration depths of a few millimetres are typical for bioturbated sediments in the coastal ocean (e.g. Wenzhöfer and Glud, 2002) and the oxygen penetration depth has been shown to increase rapidly with SFD to more than 10 cm in the deep sea (Meile and Van Cappellen, 2003; Glud, 2008). Fischer et al. (2009) and D'Hondt et al. (2015) even found cores along a transect in the South Pacific gyre being oxygenated over their entire length (up to 8 m or even 75 m, respectively), which is consistent with our model results (not shown). Simulated mean oxygen penetration depths for the six depth bin classes also agree well with observations compiled by Glud (2008) and Meile and Van Cappellen (2003, Fig. 15).
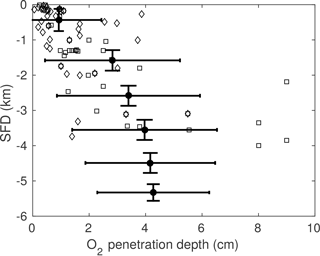
Figure 15Sea-floor depth versus O2 penetration depth for the depth-dependent parameterisation after Boudreau (1997) with . Diamonds represent observations compiled by Meile and Van Cappellen (2003) and squares observations from Glud (2008). Circles are the mean model results for the six SFD bin classes (with standard deviations). Grid cells in which the entire sediment column is oxic (i.e. zox=100 cm) are not considered in these statistics (17, 32, 102, 300, 477 and 307 cells for the six bin classes, respectively).
Because of the high computational cost associated with resolving benthic dynamics, most Earth system models of intermediate complexity (EMICs) and also some of the higher-resolution Earth system models either completely neglect or merely include a highly simplified representation of benthic–pelagic exchange processes (Hülse et al., 2017). However, benthic–pelagic coupling plays an important role for carbon cycling and the lack of its representation in EMICs compromises our ability to assess the response and recovery of the Earth system to major past, present and future carbon cycle and climate perturbations. As a consequence, there is a need for benthic biogeochemical models that are able to capture the main features of benthic biogeochemical dynamics, but that are at the same time computationally efficient enough to allow for a direct, dynamic coupling to an ocean biogeochemical model. Therefore, we have developed OMEN-SED, a one-dimensional analytical early diagenetic model that offers a predictive ability similar to complex, numerical diagenetic models at a significantly reduced computational cost.
OMEN-SED is thus not problem specific. Its reaction network resolves the most pertinent benthic biogeochemical species and the most important processes that control their cycling and burial in marine sediments. OMEN-SED can thus be coupled to a wide range of regional to global ocean biogeochemical models, EMICs and higher-resolution Earth system models to investigate a wide range of research questions associated with past, present or future carbon and macronutrient cycling. For instance, OMEN-SED can be used to (i) quantify benthic macronutrient recycling from the shallow coastal to the deep open ocean, (ii) investigate the role of benthic–pelagic coupling in the development of past or future ocean anoxia–euxinia, or to (iii) estimate global organic carbon burial in marine sediments. In theory, its scope of applicability thus ranges from the regional to the global and from the seasonal to the millennial timescale. In order to simulate organic matter preservation in the deeper sediments and thus address questions concerning long-term, geological carbon burial the degradation rate constant for the refractory OM pool has to be scaled down. The resulting larger difference between degradation rate constants can be interpreted as being needed to capture the broader range of OM reactivities degraded over the entire sediment column (see Fig. 10). Instead, more collapsed degradation rate constants are needed to model OM degradation in the upper sediments, such as the first 5 cm as shown in Sect. 4.2.2. In addition, the computational efficiency of OMEN-SED allows for the calculation of quantitative sensitivity indices requiring large sample sizes such as variance- or density-based approaches. Therefore, OMEN-SED can also help quantitatively investigate the sensitivity of benthic model output to systematic variations in model parameters when the model has been tuned to a site-specific problem.
However, OMEN-SED is inevitably associated with a certain degree of simplification that may compromise the applicability of the model in its current version under certain circumstances. First, we have assumed steady-state conditions to allow for an analytical solution to the coupled diagenetic equations. This steady-state assumption is only valid if the variability in boundary conditions and fluxes is generally longer than the characteristic timescales of the reaction–transport processes. As a consequence, OMEN-SED is well suited for coupling to EMICs and the investigation of long-term dynamics in sediment–water exchange fluxes, for instance during past extreme climate events. Yet, in its current version, OMEN-SED is not able to predict the transient response of benthic process rates and fluxes to short-term or seasonal variations in boundary conditions. Future versions of OMEN-SED could approximate non-steady-state conditions by incorporating a time-step-dependent relaxation between different steady states, similar to the schemes used in Ruardij and Van Raaphorst (1995) and Arndt and Regnier (2007). Such a pseudo-transient approach would enable the application of OMEN-SED to systems characterised by high-frequency fluctuations in boundary conditions, such as the coastal ocean or estuaries. Furthermore, by their very nature, analytical models do not allow for overlapping biogeochemical zones or depth-dependent porosity, which introduces a certain error to simulation results. However, the energy-yield-dependent sequence of oxidants is generally valid (e.g. Hensen et al., 2006) and the good agreement between OMEN-SED and the results obtained with a fully formulated numerical RTM (allowing for overlapping TEA use and depth-dependent porosity; Sect. 3.3) shows that these are not critical limitations of OMEN-SED, even for shallow sediments.
Although the model explicitly simulates DIC and alkalinity production and thus has the potential to predict pH profiles within the sediment, a major limitation at this stage is the lack of an explicit description for CaCO3 precipitation and dissolution coupled to OM decomposition, which also controls the inorganic carbon system (Krumins et al., 2013). In addition, the current version of OMEN-SED does not yet explicitly resolve iron and manganese dynamics (although note that iron is implicitly accounted for in the PO4 equation). This lack currently limits the applicability of OMEN-SED to iron- and manganese-rich environments, such as coastal marine environments, upwelling regions or ferruginous oceans. In addition, it also compromises the ability of OMEN-SED to predict H2S fluxes in Fe-rich anoxic environments, where high iron pore water concentrations can deplete pore water H2S by iron-sulfide mineral precipitation (e.g. Meyers, 2007). Therefore, already planned future extensions of OMEN-SED include an explicit description of carbonate dissolution and iron. Also note that our 1-D diffusion–bioturbation model might not be appropriate to simulate non-accumulating permeable sands of the coastal ocean.
Finally, just as all global models, the global application of OMEN-SED is complicated by the lack of an objective global framework for biogeochemical process parameterisation. The sensitivity study presented here shows that this lack is particularly critical for OM degradation rate parameters (ki, fi) and the γ values describing the completeness of secondary redox reactions. A comparison between simulated OM contents and observations indicates that a depth-dependent k−f relationship provides the best fit (Sect. 4.2.2). These results confirm that reducing the continuous distribution of organic matter reactivities into two distinct reactivity classes (2G model) requires different k−f values for shallow vs. deep ocean sediments because of the largely different reaction timescales involved (also see Fig. 10). With respect to γ values, model simulations along the global hypsometry (Sect. 3.3) have shown that high γ values generally capture the main SWI flux features, but have also highlighted that slightly lower γ values would result in a better fit of SWI fluxes to observations of the shallow ocean.
Here, we have described in detail and tested OMEN-SED, a new, analytical early diagenetic model resolving organic matter cycling and the associated biogeochemical dynamics. OMEN-SED has been explicitly designed for coupling to EMICs and combines biogeochemical complexity with computational efficiency. It is the first analytical diagenetic model to implicitly represent methanogenesis and explicitly represent oxic degradation, denitrification and sulfate reduction, as well as the reoxidation of reduced substances, adsorption and desorption, and mineral precipitation and dissolution. Explicitly resolved pore water species include O2, NO3, NH4, SO4, H2S, DIC and ALK and the solid phase includes two degradable fractions of organic matter, Fe-bound P and authigenic Ca–P minerals.
An extensive sensitive analysis based on the density-based PAWN method (Pianosi and Wagener, 2015) emphasises the importance of OM degradation rate parameters (ki, fi) and thus highlights the need for the development of an objective global framework to parameterise OM degradation rate parameters. We have shown that the performance of OMEN-SED at the system scale is similar to that of a fully formulated, multi-component numerical model. The new analytical model is able to reproduce observed pore water profiles across a wide range of depositional environments and captures observed global patterns of SWI fluxes, oxygen penetration depths, biogeochemical reaction rates and surface sediment organic matter contents. Coupled to EMICs or higher-resolution Earth system models, OMEN-SED is thus well suited to examine the role of sediments in global biogeochemical cycles in response to a wide range of past or future carbon cycle or climate perturbations over various timescales.
The OMEN-SED source code (FORTRAN and MATLAB) is provided as a Supplement to this article and is also available for download on the web (Hülse et al., 2018). A ReadMe file for the stand-alone MATLAB version of OMEN-SED describes the source code files and includes instructions for executing the model and plotting the results.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-2649-2018-supplement.
DH and SA designed and implemented the model. SD designed and implemented the boundary matching algorithm and helped with the general code development. DH and AR coupled the two models. DH carried out the simulations and analysed the results. All authors contributed to the design of the simulations, the analysis of the results and the writing of the paper.
The authors declare that they have no conflict of interest.
We would like to thank Klaus Wallmann and two anonymous
reviewers for their constructive critiques and insightful comments,
which have improved the paper. We thank Claire Reimers, Filip Meysman,
Martin Thullner, Jack Middelburg, Andy Dale, Katherina Seiter, Christof Meile, Ronny Glud
and the British Oceanographic Data Centre for supplying
the datasets and model results used in this study. We
are also grateful to Francesca Pianosi for helpful insights into sensitivity
analysis. Dominik Hülse was supported by a graduate teaching studentship by
the University of Bristol and a Heising–Simons Foundation award. Sandra Arndt acknowledges funding from the UK Natural Environmental Research Council
(NERC) grant no. NE/I021322/1 and Stuart Daines from the grants NERC JET
(NE/N018508/1) and NERC BETR (NE/P013651/1). Sandra Arndt and
Pierre Regnier were supported by funding from the
European Union Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement no. 643052 (C-CASCADES). Andy Ridgwell
was supported by a Heising–Simons Foundation award and by EU grant
ERC-2013-CoG-617313.
Edited by: Andrew Yool
Reviewed by: Klaus Wallmann and two anonymous referees
Aguilera, D. R., Jourabchi, P., Spiteri, C., and Regnier, P.: A knowledge-based reactive transport approach for the simulation of biogeochemical dynamics in Earth systems, Geochem. Geophy. Geosy., 6, Q07012, https://doi.org/10.1029/2004GC000899, 2005. a, b, c
Aller, R. C.: The importance of relict burrow structures and burrow irrigation in controlling sedimentary solute distributions, Geochim. Cosmochim. Ac., 48, 1929–1934, https://doi.org/10.1016/0016-7037(84)90375-2, 1984. a
Aller, R. C.: Benthic fauna and biogeochemical processes in marine sediments: the role of burrow structures, in: Nitrogen cycling in coastal marine environments, edited by: Blackburn, T. and Sorensen, J., Scope, Chichester, 301–338, 1988. a
Archer, D.: A data-driven model of the global calcite lysocline, Global Biogeochem. Cy., 10, 511–526, https://doi.org/10.1029/96GB01521, 1996. a, b, c, d, e
Archer, D. and Devol, A.: Benthic oxygen fluxes on the Washington shelf and slope: A comparison of in situ microelectrode and chamber flux measurements, Limnol. Oceanogr., 37, 614–629, https://doi.org/10.4319/lo.1992.37.3.0614, 1992. a
Archer, D. and Maier-Reimer, E.: Effect of Deep-Sea Sedimentary Calcite Preservation on Atmospheric Co2 Concentration, Nature, 367, 260–263, https://doi.org/10.1038/367260a0, 00506 WOS:A1994MR49400052, 1994. a, b
Archer, D., Winguth, A., Lea, D., and Mahowald, N.: What caused the glacial/interglacial atmospheric pCO2 cycles?, Rev. Geophys., 38, 159–189, https://doi.org/10.1029/1999RG000066, 2000. a
Archer, D., Eby, M., Brovkin, V., Ridgwell, A., Cao, L., Mikolajewicz, U., Caldeira, K., Matsumoto, K., Munhoven, G., Montenegro, A., and Tokos, K.: Atmospheric Lifetime of Fossil Fuel Carbon Dioxide, Annu. Rev. Earth Pl. Sc., 37, 117–134, https://doi.org/10.1146/annurev.earth.031208.100206, 2009. a, b
Archer, D. E., Morford, J. L., and Emerson, S. R.: A model of suboxic sedimentary diagenesis suitable for automatic tuning and gridded global domains, Global Biogeochem. Cy., 16, 17–1, https://doi.org/10.1029/2000GB001288, 2002. a, b
Arndt, S. and Regnier, P.: A model for the benthic-pelagic coupling of silica in estuarine ecosystems: sensitivity analysis and system scale simulation, Biogeosciences, 4, 331–352, https://doi.org/10.5194/bg-4-331-2007, 2007. a
Arndt, S., Jørgensen, B., LaRowe, D., Middelburg, J., Pancost, R., and Regnier, P.: Quantifying the degradation of organic matter in marine sediments: A review and synthesis, Earth-Sci. Rev., 123, 53–86, https://doi.org/10.1016/j.earscirev.2013.02.008, 2013. a, b, c, d, e, f, g, h, i, j
Arthur, M. A., Dean, W. E., and Pratt, L. M.: Geochemical and climatic effects of increased marine organic carbon burial at the Cenomanian/Turonian boundary, Nature, 335, 714–717, https://doi.org/10.1038/335714a0, 1988. a
Berner, R. A.: An idealized model of dissolved sulfate distribution in recent sediments, Geochim. Cosmochim. Ac., 28, 1497–1503, https://doi.org/10.1016/0016-7037(64)90164-4, 1964. a
Berner, R. A.: Early Diagenesis: A Theoretical Approach, Princeton University Press, 1980. a, b, c, d
Berner, R. A.: Sedimentary pyrite formation: An update, Geochim. Cosmochim. Ac., 48, 605–615, https://doi.org/10.1016/0016-7037(84)90089-9, 1984. a
Berner, R. A.: A model for atmospheric CO2 over Phanerozoic time, Am. J. Sci., 291, 339–376, https://doi.org/10.2475/ajs.291.4.339, 1991. a
Berner, R. A.: The Phanerozoic Carbon Cycle: CO2 and O2, Oxford University Press, 2004. a
Billen, G.: An idealized model of nitrogen recycling in marine sediments, Am. J. Sci., 282, 512–541, 1982. a, b, c, d, e
Bohlen, L., Dale, A. W., and Wallmann, K.: Simple transfer functions for calculating benthic fixed nitrogen losses and C:N:P regeneration ratios in global biogeochemical models, Global Biogeochem. Cy., 26, GB3029, https://doi.org/10.1029/2011GB004198, 2012. a
Bottrell, S. H. and Newton, R. J.: Reconstruction of changes in global sulfur cycling from marine sulfate isotopes, Earth-Sci. Rev., 75, 59–83, https://doi.org/10.1016/j.earscirev.2005.10.004, 2006. a
Boudreau, B. P.: On the equivalence of nonlocal and radial-diffusion models for porewater irrigation, J. Mar. Res., 42, 731–735, https://doi.org/10.1357/002224084788505924, 1984. a
Boudreau, B. P.: Mathematics of tracer mixing in sediments; I, Spatially-dependent, diffusive mixing, Am. J. Sci., 286, 161–198, https://doi.org/10.2475/ajs.286.3.161, 1986. a
Boudreau, B. P.: Modelling the sulfide-oxygen reaction and associated pH gradients in porewaters, Geochim. Cosmochim. Ac., 55, 145–159, https://doi.org/10.1016/0016-7037(91)90407-V, 1991. a
Boudreau, B. P.: A method-of-lines code for carbon and nutrient diagenesis in aquatic sediments, Comput. Geosci., 22, 479–496, https://doi.org/10.1016/0098-3004(95)00115-8, 1996. a, b
Boudreau, B. P.: Diagenetic models and their implementation, vol. 505, Springer Berlin, 1997. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q
Boudreau, B. P.: Mean mixed depth of sediments: The wherefore and the why, Limnol. Oceanogr., 43, 524–526, https://doi.org/10.4319/lo.1998.43.3.0524, 1998. a, b
Boudreau, B. P. and Ruddick, B. R.: On a reactive continuum representation of organic matter diagenesis, Am. J. Sci., 291, 507–538, https://doi.org/10.2475/ajs.291.5.507, 1991. a
Boudreau, B. P. and Westrich, J. T.: The dependence of bacterial sulfate reduction on sulfate concentration in marine sediments, Geochim. Cosmochim. Ac., 48, 2503–2516, https://doi.org/10.1016/0016-7037(84)90301-6, 1984. a, b
Boudreau, B. P., Mucci, A., Sundby, B., Luther, G. W., and Silverberg, N.: Comparative diagenesis at three sites on the Canadian continental margin, J. Mar. Res., 56, 1259–1284, https://doi.org/10.1357/002224098765093634, 1998. a
Boudreau, B. P., Arnosti, C., Jørgensen, B. B., and Canfield, D. E.: Comment on “Physical Model for the Decay and Preservation of Marine Organic Carbon”, Science, 319, 1616–1616, https://doi.org/10.1126/science.1148589, 2008. a
Broecker, W. S.: Ocean chemistry during glacial time, Geochim. Cosmochim. Ac., 46, 1689–1705, https://doi.org/10.1016/0016-7037(82)90110-7, 1982. a
Burdige, D. J.: Geochemistry of marine sediments, vol. 398, Princeton University Press Princeton, 2006. a
Burdige, D. J.: Preservation of Organic Matter in Marine Sediments: Controls, Mechanisms, and an Imbalance in Sediment Organic Carbon Budgets?, Chem. Rev., 107, 467–485, https://doi.org/10.1021/cr050347q, 2007. a
Burwicz, E. B., Rüpke, L. H., and Wallmann, K.: Estimation of the global amount of submarine gas hydrates formed via microbial methane formation based on numerical reaction-transport modeling and a novel parameterization of Holocene sedimentation, Geochim. Cosmochim. Ac., 75, 4562–4576, https://doi.org/10.1016/j.gca.2011.05.029, 2011. a, b
Canfield, D. E., Kristensen, E., and Thamdrup, B.: Aquatic Geomicrobiology, Gulf Professional Publishing, 2005. a, b
Colbourn, G., Ridgwell, A., and Lenton, T. M.: The Rock Geochemical Model (RokGeM) v0.9, Geosci. Model Dev., 6, 1543–1573, https://doi.org/10.5194/gmd-6-1543-2013, 2013. a
Conkright, M. E., Locarnini, R. A., Garcia, H. E., O'Brien, T. D., Boyer, T. P., Stephens, C., and Antonov, J. I.: World Ocean Atlas 2001: Objective analyses, data statistics, and figures: CD-ROM documentation, US Department of Commerce, National Oceanic and Atmospheric Administration, National Oceanographic Data Center, Ocean Climate Laboratory, 2002. a
Devol, A. H. and Christensen, J. P.: Benthic fluxes and nitrogen cycling in sediments of the continental margin of the eastern North Pacific, J. Mar. Res., 51, 345–372, https://doi.org/10.1357/0022240933223765, 1993. a, b
D'Hondt, S., Inagaki, F., Zarikian, C. A., Abrams, L. J., Dubois, N., Engelhardt, T., Evans, H., Ferdelman, T., Gribsholt, B., Harris, R. N., Hoppie, B. W., Hyun, J.-H., Kallmeyer, J., Kim, J., Lynch, J. E., McKinley, C. C., Mitsunobu, S., Morono, Y., Murray, R. W., Pockalny, R., Sauvage, J., Shimono, T., Shiraishi, F., Smith, D. C., Smith-Duque, C. E., Spivack, A. J., Steinsbu, B. O., Suzuki, Y., Szpak, M., Toffin, L., Uramoto, G., Yamaguchi, Y. T., Zhang, G.-l., Zhang, X.-H., and Ziebis, W.: Presence of oxygen and aerobic communities from sea floor to basement in deep-sea sediments, Nat. Geosci., 8, 299–304, https://doi.org/10.1038/ngeo2387, 2015. a
Edwards, N. R. and Marsh, R.: Uncertainties due to transport-parameter sensitivity in an efficient 3-D ocean-climate model, Clim. Dynam., 24, 415–433, https://doi.org/10.1007/s00382-004-0508-8, 2005. a
Emerson, S. and Bender, M. L.: Carbon fluxes at the sediment-water interface of the deep-sea: calcium carbonate preservation, J. Mar. Res., 39, 139–162, 1981. a
Emerson, S. and Hedges, J. I.: Processes controlling the organic carbon content of open ocean sediments, Paleoceanography, 3, 621–634, https://doi.org/10.1029/PA003i005p00621, 1988. a
Emerson, S., Jahnke, R., and Heggie, D.: Sediment-water exchange in shallow water estuarine sediments, J. Mar. Res., 42, 709–730, https://doi.org/10.1357/002224084788505942, 1984. a
Epping, E., van der Zee, C., Soetaert, K., and Helder, W.: On the oxidation and burial of organic carbon in sediments of the Iberian margin and Nazaré Canyon (NE Atlantic), Prog. Oceanogr., 52, 399–431, https://doi.org/10.1016/S0079-6611(02)00017-4, 2002. a, b, c, d, e
Fischer, J. P., Ferdelman, T. G., D'Hondt, S., Røy, H., and Wenzhöfer, F.: Oxygen penetration deep into the sediment of the South Pacific gyre, Biogeosciences, 6, 1467–1478, https://doi.org/10.5194/bg-6-1467-2009, 2009. a
Glud, R. N.: Oxygen dynamics of marine sediments, Mar. Biol. Res., 4, 243–289, https://doi.org/10.1080/17451000801888726, 2008. a, b, c
Goloway, F. and Bender, M.: Diagenetic models of interstitial nitrate profiles in deep sea suboxic sediments, Limnol. Oceanogr., 27, 624–638, https://doi.org/10.4319/lo.1982.27.4.0624, 1982. a, b, c, d, e
Goosse, H., Brovkin, V., Fichefet, T., Haarsma, R., Huybrechts, P., Jongma, J., Mouchet, A., Selten, F., Barriat, P.-Y., Campin, J.-M., Deleersnijder, E., Driesschaert, E., Goelzer, H., Janssens, I., Loutre, M.-F., Morales Maqueda, M. A., Opsteegh, T., Mathieu, P.-P., Munhoven, G., Pettersson, E. J., Renssen, H., Roche, D. M., Schaeffer, M., Tartinville, B., Timmermann, A., and Weber, S. L.: Description of the Earth system model of intermediate complexity LOVECLIM version 1.2, Geosci. Model Dev., 3, 603–633, https://doi.org/10.5194/gmd-3-603-2010, 2010. a
Gypens, N., Lancelot, C., and Soetaert, K.: Simple parameterisations for describing N and P diagenetic processes: Application in the North Sea, Prog. Oceanogr., 76, 89–110, https://doi.org/10.1016/j.pocean.2007.10.003, 2008. a, b, c, d, e, f, g, h, i
Heinze, C., Maier-Reimer, E., Winguth, A. M. E., and Archer, D.: A global oceanic sediment model for long-term climate studies, Global Biogeochem. Cy., 13, 221–250, https://doi.org/10.1029/98GB02812, 1999. a, b, c
Hensen, C., Zabel, M., and Schulz, H. N.: Benthic Cycling of Oxygen, Nitrogen and Phosphorus, in: Marine Geochemistry, edited by: Schulz, H. D. and Zabel, M., Springer Berlin Heidelberg, 207–240, 2006. a, b, c
Hülse, D., Arndt, S., Wilson, J. D., Munhoven, G., and Ridgwell, A.: Understanding the causes and consequences of past marine carbon cycling variability through models, Earth-Sci. Rev., 171, 349–382, https://doi.org/10.1016/j.earscirev.2017.06.004, 2017. a, b, c, d
Hülse, D., Arndt, S., Daines, S., Regnier, P., and Ridgwell, A.: OMEN-SED 1.0 model code, Zenodo, https://doi.org/10.5281/zenodo.1292930, 2018. a
Ilyina, T., Six, K. D., Segschneider, J., Maier-Reimer, E., Li, H., and Núñez-Riboni, I.: Global ocean biogeochemistry model HAMOCC: Model architecture and performance as component of the MPI-Earth system model in different CMIP5 experimental realizations, J. Adv. Model. Earth Sy., 5, 287–315, https://doi.org/10.1029/2012MS000178, 2013. a, b
Ingall, E. and Jahnke, R.: Evidence for enhanced phosphorus regeneration from marine sediments overlain by oxygen depleted waters, Geochim. Cosmochim. Ac., 58, 2571–2575, https://doi.org/10.1016/0016-7037(94)90033-7, 1994. a
Jarvis, I., Lignum, J. S., Gröcke, D. R., Jenkyns, H. C., and Pearce, M. A.: Black shale deposition, atmospheric CO2 drawdown, and cooling during the Cenomanian-Turonian Oceanic Anoxic Event, Paleoceanography, 26, PA3201, https://doi.org/10.1029/2010PA002081, 2011. a
Jenkyns, H. C.: Geochemistry of oceanic anoxic events, Geochem. Geophy. Geosy., 11, Q03004, https://doi.org/10.1029/2009GC002788, 2010. a
Jørgensen, B. B.: A comparison of methods for the quantification of bacterial sulfate reduction in coastal marine sediments: II Calculation from mathematical models, Geomicrobiol. J., 1, 29–47, https://doi.org/10.1080/01490457809377722, 1978. a, b
Jørgensen, B. B. and Kasten, S.: Sulfur Cycling and Methane Oxidation, in: Marine Geochemistry, edited by: Schulz, P. D. H. D. and Zabel, D. M., pp. 271–309, Springer Berlin Heidelberg, 2006. a
Jourabchi, P., Cappellen, P. V., and Regnier, P.: Quantitative interpretation of pH distributions in aquatic sediments: A reaction-transport modeling approach, Am. J. Sci., 305, 919–956, https://doi.org/10.2475/ajs.305.9.919, 2005. a, b, c
Karstensen, J., Stramma, L., and Visbeck, M.: Oxygen minimum zones in the eastern tropical Atlantic and Pacific oceans, Prog. Oceanogr., 77, 331–350, 2008. a
Kolmogorov, A.: Sulla determinazione empirica di una leggi di distribuzione, Giorn. 1st Ital. Attuari, 4, 91, 1933. a
Krom, M. D. and Berner, R. A.: Adsorption of phosphate in anoxic marine sediments, Limnol. Oceanogr., 25, 797–806, https://doi.org/10.4319/lo.1980.25.5.0797, 1980. a
Krumins, V., Gehlen, M., Arndt, S., Van Cappellen, P., and Regnier, P.: Dissolved inorganic carbon and alkalinity fluxes from coastal marine sediments: model estimates for different shelf environments and sensitivity to global change, Biogeosciences, 10, 371–398, https://doi.org/10.5194/bg-10-371-2013, 2013. a, b, c
Lee, C., Wakeham, S. G., and I. Hedges, J.: Composition and flux of particulate amino acids and chloropigments in equatorial Pacific seawater and sediments, Deep-Sea Res. Pt I, 47, 1535–1568, https://doi.org/10.1016/S0967-0637(99)00116-8, 2000. a, b
Lenton, T. M. and Watson, A. J.: Redfield revisited: 1. Regulation of nitrate, phosphate, and oxygen in the ocean, Global Biogeochem. Cy., 14, 225–248, https://doi.org/10.1029/1999GB900065, 2000. a
Li, Y.-H. and Gregory, S.: Diffusion of ions in sea water and in deep-sea sediments, Geochim. Cosmochim. Ac., 38, 703–714, https://doi.org/10.1016/0016-7037(74)90145-8, 1974. a, b
Longhurst, A., Sathyendranath, S., Platt, T., and Caverhill, C.: An estimate of global primary production in the ocean from satellite radiometer data, J. Plankton Res., 17, 1245–1271, https://doi.org/10.1093/plankt/17.6.1245, 1995. a
Mackenzie, F. T.: Sediments, Diagenesis, and Sedimentary Rocks: Treatise on Geochemistry, Second Edition, Elsevier, 2005. a
Meile, C. and Van Cappellen, P.: Global estimates of enhanced solute transport in marine sediments, Limnol. Oceanogr., 48, 777–786, https://doi.org/10.4319/lo.2003.48.2.0777, 2003. a, b, c
Meyers, S. R.: Production and preservation of organic matter: The significance of iron, Paleoceanography, 22, PA4211, https://doi.org/10.1029/2006PA001332, 2007. a
Meysman, F. J. R., Middelburg, J. J., Herman, P. M. J., and Heip, C. H. R.: Reactive transport in surface sediments. II. Media: an object-oriented problem-solving environment for early diagenesis, Comput. Geosci., 29, 301–318, https://doi.org/10.1016/S0098-3004(03)00007-4, 2003. a, b, c, d
Middelburg, J. J.: A simple rate model for organic matter decomposition in marine sediments, Geochim. Cosmochim. Ac., 53, 1577–1581, https://doi.org/10.1016/0016-7037(89)90239-1, 1989. a
Middelburg, J. J., Vlug, T., Jaco, F., and van der Nat, W. A.: Organic matter mineralization in marine systems, Global Planet. Change, 8, 47–58, https://doi.org/10.1016/0921-8181(93)90062-S, 1993. a, b, c
Middelburg, J. J., Soetaert, K., Herman, P. M. J., and Heip, C. H. R.: Denitrification in marine sediments: A model study, Global Biogeochem. Cy., 10, 661–673, https://doi.org/10.1029/96GB02562, 1996. a, b, c, d, e
Middelburg, J. J., Soetaert, K., and Herman, P. M.: Empirical relationships for use in global diagenetic models, Deep-Sea Res. Pt. I, 44, 327–344, https://doi.org/10.1016/S0967-0637(96)00101-X, 1997. a, b, c, d, e, f, g, h
Morrison, J. M., Codispoti, L. A., Smith, S. L., Wishner, K., Flagg, C., Gardner, W. D., Gaurin, S., Naqvi, S., Manghnani, V., Prosperie, L., and Gundersen, J. S.: The oxygen minimum zone in the Arabian Sea during 1995, Deep-Sea Res. Pt. II, 46, 1903–1931, 1999. a
Mort, H. P., Adatte, T., Föllmi, K. B., Keller, G., Steinmann, P., Matera, V., Berner, Z., and Stüben, D.: Phosphorus and the roles of productivity and nutrient recycling during oceanic anoxic event 2, Geology, 35, 483–486, https://doi.org/10.1130/G23475A.1, 2007. a
Munhoven, G.: Glacial–interglacial rain ratio changes: Implications for atmospheric and ocean–sediment interaction, Deep-Sea Res. Pt II, 54, 722–746, https://doi.org/10.1016/j.dsr2.2007.01.008, 2007. a, b, c
Najjar, R. G., Jin, X., Louanchi, F., Aumont, O., Caldeira, K., Doney, S. C., Dutay, J.-C., Follows, M., Gruber, N., Joos, F., Lindsay, K., Maier-Reimer, E., Matear, R. J., Matsumoto, K., Monfray, P., Mouchet, A., Orr, J. C., Plattner, G.-K., Sarmiento, J. L., Schlitzer, R., Slater, R. D., Weirig, M.-F., Yamanaka, Y., and Yool, A.: Impact of circulation on export production, dissolved organic matter, and dissolved oxygen in the ocean: Results from Phase II of the Ocean Carbon-cycle Model Intercomparison Project (OCMIP-2), Global Biogeochem. Cy., 21, GB3007, https://doi.org/10.1029/2006GB002857, 2007. a
Palastanga, V., Slomp, C. P., and Heinze, C.: Long-term controls on ocean phosphorus and oxygen in a global biogeochemical model, Global Biogeochem. Cy., 25, GB3024, https://doi.org/10.1029/2010GB003827, 2011. a, b, c, d, e, f
Pianosi, F. and Wagener, T.: A simple and efficient method for global sensitivity analysis based on cumulative distribution functions, Environ. Modell. Softw., 67, 1–11, https://doi.org/10.1016/j.envsoft.2015.01.004, 2015. a, b, c
Pianosi, F., Sarrazin, F., and Wagener, T.: A Matlab toolbox for Global Sensitivity Analysis, Environ. Modell. Softw., 70, 80–85, https://doi.org/10.1016/j.envsoft.2015.04.009, 2015. a
Pianosi, F., Beven, K., Freer, J., Hall, J. W., Rougier, J., Stephenson, D. B., and Wagener, T.: Sensitivity analysis of environmental models: A systematic review with practical workflow, Environ. Modell. Softw., 79, 214–232, https://doi.org/10.1016/j.envsoft.2016.02.008, 2016. a, b, c
Redfield, A. C.: The influence of organisms on the composition of seawater, The sea, 2, 26–77, 1963. a
Reeburgh, W. S.: Oceanic Methane Biogeochemistry, Chem. Rev., 107, 486–513, https://doi.org/10.1021/cr050362v, 2007. a
Regnier, P., Dale, A. W., Arndt, S., LaRowe, D. E., Mogollón, J., and Van Cappellen, P.: Quantitative analysis of anaerobic oxidation of methane (AOM) in marine sediments: A modeling perspective, Earth-Sci. Rev., 106, 105–130, https://doi.org/10.1016/j.earscirev.2011.01.002, 2011. a
Reimers, C. E., Lange, C. B., Tabak, M., and Bernhard, J. M.: Seasonal spillover and varve formation in the Santa Barbara Basin, California, Limnol. Oceanogr., 35, 1577–1585, https://doi.org/10.4319/lo.1990.35.7.1577, 1990. a, b
Reimers, C. E., Ruttenberg, K. C., Canfield, D. E., Christiansen, M. B., and Martin, J. B.: Porewater pH and authigenic phases formed in the uppermost sediments of the Santa Barbara Basin, Geochim. Cosmochim. Ac., 60, 4037–4057, https://doi.org/10.1016/S0016-7037(96)00231-1, 1996. a, b, c, d, e, f
Ridgwell, A. and Hargreaves, J. C.: Regulation of atmospheric CO2 by deep-sea sediments in an Earth system model, Global Biogeochem. Cy., 21, GB2008, https://doi.org/10.1029/2006GB002764, 2007. a, b, c
Ridgwell, A. and Zeebe, R. E.: The role of the global carbonate cycle in the regulation and evolution of the Earth system, Earth Planet. Sc. Lett., 234, 299–315, https://doi.org/10.1016/j.epsl.2005.03.006, 2005. a
Ridgwell, A., Hargreaves, J. C., Edwards, N. R., Annan, J. D., Lenton, T. M., Marsh, R., Yool, A., and Watson, A.: Marine geochemical data assimilation in an efficient Earth System Model of global biogeochemical cycling, Biogeosciences, 4, 87–104, https://doi.org/10.5194/bg-4-87-2007, 2007. a, b, c, d, e, f
Ruardij, P. and Van Raaphorst, W.: Benthic nutrient regeneration in the ERSEM ecosystem model of the North Sea, Neth. J. Sea Res., 33, 453–483, https://doi.org/10.1016/0077-7579(95)90057-8, 1995. a, b, c, d, e, f
Ruttenberg, K. C.: Reassessment of the oceanic residence time of phosphorus, Chem. Geol., 107, 405–409, https://doi.org/10.1016/0009-2541(93)90220-D, 1993. a
Schulz, H. D.: Quantification of Early Diagenesis: Dissolved Constituents in Pore Water and Signals in the Solid Phase, in: Marine Geochemistry, edited by: Schulz, P. D. H. D. and Zabel, D. M., 73–124, Springer Berlin Heidelberg, 2006. a, b, c, d, e
Seiter, K., Hensen, C., Schröter, J., and Zabel, M.: Organic carbon content in surface sediments–defining regional provinces, Deep-Sea Res. Pt. I, 51, 2001–2026, https://doi.org/10.1016/j.dsr.2004.06.014, 2004. a, b, c, d, e, f, g
Shaffer, G., Malskær Olsen, S., and Pepke Pedersen, J. O.: Presentation, calibration and validation of the low-order, DCESS Earth System Model (Version 1), Geosci. Model Dev., 1, 17–51, https://doi.org/10.5194/gmd-1-17-2008, 2008. a, b, c
Slomp, C., Malschaert, J., and Van Raaphorst, W.: The role of adsorption in sediment-water exchange of phosphate in North Sea continental margin sediments, Limnol. Oceanogr., 43, 832–846, 1998. a, b, c, d
Slomp, C. P., Epping, E. H., Helder, W., and Van Raaphorst, W.: A key role for iron-bound phosphorus in authigenic apatite formation in North Atlantic continental platform sediments, J. Mar. Res., 54, 1179–1205, https://doi.org/10.1357/0022240963213745, 1996. a, b, c, d, e, f, g
Smirnov, N. V.: On the estimation of the discrepancy between empirical curves of distribution for two independent samples, Bull. Math. Univ. Moscou, 2, 1939. a
Soetaert, K., Herman, P. M. J., and Middelburg, J. J.: A model of early diagenetic processes from the shelf to abyssal depths, Geochim. Cosmochim. Ac., 60, 1019–1040, https://doi.org/10.1016/0016-7037(96)00013-0, 1996. a, b, c, d, e, f, g, h
Soetaert, K., Middelburg, J. J., Herman, P. M. J., and Buis, K.: On the coupling of benthic and pelagic biogeochemical models, Earth-Sci. Rev., 51, 173–201, https://doi.org/10.1016/S0012-8252(00)00004-0, 2000. a, b
Stein, R., Rullkötter, J., and Welte, D. H.: Accumulation of organic-carbon-rich sediments in the Late Jurassic and Cretaceous Atlantic Ocean – A synthesis, Chem. Geol., 56, 1–32, https://doi.org/10.1016/0009-2541(86)90107-5, 1986. a
Stolpovsky, K., Dale, A. W., and Wallmann, K.: Toward a parameterization of global-scale organic carbon mineralization kinetics in surface marine sediments, Global Biogeochem. Cy., 29, 2015GB005087, https://doi.org/10.1002/2015GB005087, 2015. a, b, c, d, e, f
Stolpovsky, K., Dale, A. W., and Wallmann, K.: A new look at the multi-G model for organic carbon degradation in surface marine sediments for coupled benthic–pelagic simulations of the global ocean, Biogeosciences, 15, 3391–3407, https://doi.org/10.5194/bg-15-3391-2018, 2018. a
Stumm, W. and Morgan, J. J.: Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, John Wiley & Sons, 2012. a
Teal, L., Bulling, M., Parker, E., and Solan, M.: Global patterns of bioturbation intensity and mixed depth of marine soft sediments, Aquat. Biol., 2, 207–218, https://doi.org/10.3354/ab00052, 2010. a, b
Thullner, M., Van Cappellen, P., and Regnier, P.: Modeling the impact of microbial activity on redox dynamics in porous media, Geochim. Cosmochim. Ac., 69, 5005–5019, https://doi.org/10.1016/j.gca.2005.04.026, 2005. a
Thullner, M., Dale, A. W., and Regnier, P.: Global-scale quantification of mineralization pathways in marine sediments: A reaction-transport modeling approach, Geochem. Geophy. Geosy., 10, Q10012, https://doi.org/10.1029/2009GC002484, 2009. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Tjiputra, J. F., Roelandt, C., Bentsen, M., Lawrence, D. M., Lorentzen, T., Schwinger, J., Seland, Ø., and Heinze, C.: Evaluation of the carbon cycle components in the Norwegian Earth System Model (NorESM), Geosci. Model Dev., 6, 301–325, https://doi.org/10.5194/gmd-6-301-2013, 2013. a
Toth, D. J. and Lerman, A.: Organic matter reactivity and sedimentation rates in the ocean, Am. J. Sci., 277, 465–485, https://doi.org/10.2475/ajs.277.4.465, 1977. a
Tromp, T. K., Van Cappellen, P., and Key, R. M.: A global model for the early diagenesis of organic carbon and organic phosphorus in marine sediments, Geochim. Cosmochim. Ac., 59, 1259–1284, https://doi.org/10.1016/0016-7037(95)00042-X, 1995. a, b, c, d, e, f
Tsandev, I. and Slomp, C.: Modeling phosphorus cycling and carbon burial during Cretaceous Oceanic Anoxic Events, Earth Planet. Sc. Lett., 286, 71–79, https://doi.org/10.1016/j.epsl.2009.06.016, 2009. a
Ullman, W. J. and Aller, R. C.: Diffusion coefficients in nearshore marine sediments, Limnol. Oceanogr., 27, 552–556, https://doi.org/10.4319/lo.1982.27.3.0552, 1982. a
Van Cappellen, P. and Berner, R. A.: A mathematical model for the early diagenesis of phosphorus and fluorine in marine sediments; apatite precipitation, Am. J. Sci., 288, 289–333, https://doi.org/10.2475/ajs.288.4.289, 1988. a, b
Van Cappellen, P. and Ingall, E. D.: Benthic phosphorus regeneration, net primary production, and ocean anoxia: A model of the coupled marine biogeochemical cycles of carbon and phosphorus, Paleoceanography, 9, 677–692, https://doi.org/10.1029/94PA01455, 1994. a, b, c
Van Cappellen, P. and Wang, Y.: Metal cycling in surface sediments: modeling the interplay of transport and reaction, Metal contaminated aquatic sediments, 21–64, 1995. a, b
Van Cappellen, P. and Wang, Y.: Cycling of iron and manganese in surface sediments; a general theory for the coupled transport and reaction of carbon, oxygen, nitrogen, sulfur, iron, and manganese, Am. J. Sci., 296, 197–243, https://doi.org/10.2475/ajs.296.3.197, 1996. a, b, c, d
van Weering, T. C. E., de Stigter, H. C., Boer, W., and de Haas, H.: Recent sediment transport and accumulation on the NW Iberian margin, Prog. Oceanogr., 52, 349–371, https://doi.org/10.1016/S0079-6611(02)00015-0, 2002. a
Vanderborght, J.-P. and Billen, G.: Vertical distribution of nitrate concentration in interstitial water of marine sediments with nitrification and denitrification, Limnol. Oceanogr., 20, 953–961, https://doi.org/10.4319/lo.1975.20.6.0953, 1975. a, b, c
Vanderborght, J.-P., Wollas, R., and Bitten, G.: Kinetic models of diagenesis in disturbed sediments. Part 2. Nitrogen diagenesis, Limnol. Oceanogr., 22, 794–803, https://doi.org/10.4319/lo.1977.22.5.0794, 1977. a, b
Wakeham, S. G., Hedges, J. I., Lee, C., Peterson, M. L., and Hernes, P. J.: Compositions and transport of lipid biomarkers through the water column and surficial sediments of the equatorial Pacific Ocean, Deep Sea Research Part II: Topical Studies in Oceanography, 44, 2131–2162, https://doi.org/10.1016/S0967-0645(97)00035-0, 1997. a, b
Wang, Y. and Van Cappellen, P.: A multicomponent reactive transport model of early diagenesis: Application to redox cycling in coastal marine sediments, Geochim. Cosmochim. Ac., 60, 2993–3014, https://doi.org/10.1016/0016-7037(96)00140-8, 1996. a, b, c, d
Wenzhöfer, F. and Glud, R. N.: Benthic carbon mineralization in the Atlantic: a synthesis based on in situ data from the last decade, Deep-Sea Res. Pt. I, 49, 1255–1279, https://doi.org/10.1016/S0967-0637(02)00025-0, 2002. a
Wolf-Gladrow, D. A., Zeebe, R. E., Klaas, C., Körtzinger, A., and Dickson, A. G.: Total alkalinity: The explicit conservative expression and its application to biogeochemical processes, Mar. Chem., 106, 287–300, https://doi.org/10.1016/j.marchem.2007.01.006, 2007. a
- Abstract
- Introduction
- Model description
- Stand-alone sensitivity analysis and case studies
- Coupled pre-industrial Earth system model simulations
- Scope of applicability and model limitations
- Conclusions
- Code availability
- Appendix A: Reaction network
- Appendix B: Sensitivity analysis
- Appendix C: Prescribed burial flux fields
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Model description
- Stand-alone sensitivity analysis and case studies
- Coupled pre-industrial Earth system model simulations
- Scope of applicability and model limitations
- Conclusions
- Code availability
- Appendix A: Reaction network
- Appendix B: Sensitivity analysis
- Appendix C: Prescribed burial flux fields
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement