2.1 Model grid and bathymetry

The hierarchy of resolutions is based on the “ORCA” family of global grids within the NEMO framework (Madec, 2016), specifically ORCA1, ORCA025 and ORCA12. These have nominal 1, 1∕4 and $\mathrm{1}/{\mathrm{12}}^{\circ }$ resolution at the Equator and an isotropic Mercator grid in which the meridional grid spacing is reduced to match the reduction in the zonal grid spacing in the poleward direction. In the Northern Hemisphere there is a quasi-isotropic bipolar grid with poles at land points in Siberia and Canada. The ORCA1 model has increased resolution in the meridional direction near the Equator. In the Southern Hemisphere, the grids have been extended southwards compared to the original versions⁷ with the southern limit changed from 77 to 85^∘ S to permit the modelling of the circulation under ice shelves in Antarctica. A simple extension of the Mercator grid southwards would result in very small grid spacings at the southernmost points giving a severe CFL limit on the time step. An alternative procedure described in Mathiot et al. (2017) is therefore used, whereby segments of the Northern Hemisphere bipolar part of the grid are scaled and joined to the southern edge of the existing grid.

The three models share a common set of 75 vertical levels (Culverwell, 2009). The level thickness is 1 m near the surface and 200 m at depth, increasing as a double tanh function. This gives a balance between high resolution near the surface to resolve short-term ocean responses to atmospheric forcing and reasonable resolution in the thermocline. Stewart et al. (2017) show that 75 levels is the minimum number capable of resolving the second baroclinic mode. Cells spanning partial model levels are allowed next to the bathymetry (Barnier et al., 2006; Adcroft et al., 1997).

Table 1Table giving GO6 parameters and settings that vary between resolutions.

Download Print Version | Download XLSX

The model bathymetries for each of the three resolutions were derived from different data sets; in this respect the hierarchy of resolutions is not yet fully traceable. The ORCA1 bathymetry is derived from the ETOPO2 data set (NOAA, 2006) with the bathymetry on the Antarctic shelf based on IBSCO (Arndt et al., 2013). For ORCA025, the bathymetry is derived from the ETOPO1 data set (Amante and Eakins, 2009) with modifications in coastal regions based on GEBCO (IOC, IHO and BODC, 2003) and the bathymetry on the Antarctic shelf derived from IBSCO (Arndt et al., 2013). For ORCA12 the bathymetry is derived from GEBCO_2014 (Weatherall et al., 2015).

2.2 Free surface solution and advection

The model uses a nonlinear free surface in which the cell thicknesses throughout the water column are allowed to vary with time (the z^* coordinate of Adcroft and Campin, 2004). This permits an exact representation of the surface fresh water flux. The equation for the surface pressure gradient is solved using a filtered solution in which the fast gravity waves are damped by an additional force in the equation (Roullet and Madec, 2000).

The momentum advection term is a vector-invariant formulation in which the horizontal advection is split into rotational and irrotational parts. The vorticity term (including the Coriolis term) is calculated using the energy and enstrophy conserving scheme of Arakawa and Lamb (1981). There are two versions of this scheme in NEMO which differ according to how the topography boundary condition is handled. For GO6 we choose the ln_dynvor_een_old=true option which reinforces the tendency of the flow to follow isobaths (Madec, 2016, Sect. 6.2). This is the same option that was used for GO5. The irrotational part of the momentum advection is formulated according to Hollingsworth et al. (1983) in order to avoid vertical numerical instabilities. Advection of tracers is done using the total variance diminishing (TVD) scheme of Zalesak (1979).

2.3 Mixing and boundary conditions

Lateral diffusion of momentum is on geopotential surfaces and uses a Laplacian viscosity in ORCA1 and a bi-Laplacian viscosity in ORCA025 and ORCA12 with coefficients given in Table 1. The viscosity coefficients reduce polewards – linearly with grid size for the Laplacian and with the cube of the grid length for the bi-Laplacian – in order to avoid numerical diffusion instabilities. Lateral diffusion of tracers is along isoneutral surfaces using Laplacian mixing with coefficients given in Table 1. For ORCA1, a parameterization of adiabatic eddy mixing (Gent and Mcwilliams, 1990) with a spatially varying coefficient (Held and Larichev, 1996) is used, but this is not included in ORCA025 or ORCA12. A free slip lateral boundary condition on momentum is applied at all resolutions. For the 1∕4 and $\mathrm{1}/{\mathrm{12}}^{\circ }$ configurations, the momentum boundary condition is changed around the coastline of Antarctica to a partial slip condition at $\mathrm{1}/{\mathrm{4}}^{\circ }$ and a no-slip condition at $\mathrm{1}/{\mathrm{12}}^{\circ }$. This is to avoid instabilities associated with artificial cliffs in the bathymetry at the edge of the ice shelves where the ice cavities have been closed.

The vertical mixing of tracers and momentum is parameterized using a modified version of the Gaspar et al. (1990) turbulent kinetic energy (TKE) scheme (Madec, 2016). Unresolved mixing due to internal wave breaking is represented by a background vertical eddy diffusivity of $\mathrm{1.2}\times {\mathrm{10}}^{-\mathrm{5}}$ m² s⁻¹, which decreases linearly from $\pm {\mathrm{15}}^{\circ }$ latitude to a value of $\mathrm{1.2}\times {\mathrm{10}}^{-\mathrm{6}}$ m² s⁻¹ at $\pm {\mathrm{5}}^{\circ }$ latitude (Gregg et al., 2003) and a globally constant background viscosity of $\mathrm{1.2}\times {\mathrm{10}}^{-\mathrm{4}}$ m² s⁻¹. Additionally there is enhanced mixing at the surface depending on the wind stress to represent mixing due to surface wave breaking (Craig and Banner, 1994), a representation of Langmuir cell mixing (Axell, 2002), and an ad hoc representation of mixing due to near-inertial wave breaking (Rodgers et al., 2014). This latter term has an associated length scale which can be varied geographically. This was tuned in GO5 (Megann et al., 2014) and further tuning of this term has taken place as part of the development of GO6, which is described in Sect. 4.3.

Convection in the model is parameterized as an enhanced vertical diffusivity of 10 m² s⁻¹ for momentum and tracer fields where the water column is unstable. A parameterization of double diffusive mixing is included (Merryfield et al., 1999). A climatological geothermal heat flux due to Stein and Stein (1992) is used as a bottom boundary condition. A quadratic bottom friction is used with increased friction in the Indonesian Throughflow, Denmark Strait and Bab-el-Mandeb regions. The bottom boundary layer scheme of Beckmann and Döscher (1997) is used with advective and diffusive components. The tidal mixing parameterization of Simmons et al. (2004) is included with a special formulation for the Indonesian Throughflow (Koch-Larrouy et al., 2008).

2.4 Fresh water input from land

Fresh water runoff from land is input in the surface layer of the ocean with the assumption that the runoff is fresh and at the same temperature as the local sea surface temperature. An enhanced vertical mixing of $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{3}}$ m² s⁻¹ is added over the top 10 m of the water column at runoff points to mix the runoff vertically and avoid instabilities associated with very shallow fresh layers at the surface. Fresh water input from ice sheets in Greenland and Antarctica is modelled using a Lagrangian iceberg scheme and a parameterization of ice shelf basal melting .

The Lagrangian iceberg model is that of Bigg et al. (1997) and Martin and Adcroft (2010), which was implemented in NEMO by Marsh et al. (2015). Icebergs are represented by Lagrangian particles with each particle representing a collection of icebergs within a given size range. The momentum balance for icebergs comprises the Coriolis force, air and water form drags, the horizontal pressure gradient force and a wave radiation force. The mass balance for an individual iceberg is governed by basal melting, buoyant convection at the sidewalls and wave erosion. While this model gives a reasonable approximation of iceberg behaviour, there are a number of weaknesses. Firstly, the icebergs only exchange heat and fresh water with the surface layer of the ocean (of 1 m thickness in GO6) and are advected by surface currents, whereas in reality many icebergs have draughts of hundreds of metres and so will interact with the ocean at depth. Secondly, there is no momentum exchange with sea ice. Thirdly, while the latent heat of melting is extracted from the ocean, the heat content of the meltwater input to the ocean is neglected.

The extended versions of the ORCA grids and developments in the NEMO 3.6 code make it possible to model the ocean circulation beneath the major ice shelves around Antarctica (Mathiot et al., 2017). In the GO6 configuration we close these cavities and prescribe climatological fresh water input through depth at the edge of the ice shelves to mimic the effect of ice shelf basal melt on the wider circulation, a parameterization described in Mathiot et al. (2017). In GO7 the cavities are open and climatological melting is prescribed at the bottom of the ice shelf.

2.5 Sea ice model

For the CORE2-forced experiments described in this paper, GO6 and GO7 are run with the GSI8.1 configuration of the Los Alamos National Laboratory sea ice model CICE. The GSI8.1 configuration is described in detail by Ridley et al. (2018). It consists of version 5.2.1 of the CICE base code with multi-layer, energy-conserving thermodynamics (Bitz and Lipscomb, 1999), elastic-viscous-plastic ice rheology (Hunke and Dukowicz, 1997) and multi-category ice thickness (Bitz et al., 2001) with 5 thickness categories. The multi-layer thermodynamics uses four layers of ice and one layer of snow. The impact of surface melt ponds is included, with the melt pond fraction and depth calculated using the topographic melt pond model of Flocco et al. (2010). The freezing point of the ocean is dependent on the local salinity. Ridley et al. (2018) describe tests of GSI8.1 within the context of the GC3.1 coupled model (Williams et al., 2017). In the coupled configuration the sea ice thermodynamics calculation is split, with the internal sea ice thermodynamics being solved in CICE but the surface energy balance solved in the land surface model JULES as described by West et al. (2016). For the forced experiments described in this paper, the sea ice thermodynamics and radiative transfer are solved entirely within the sea ice model component. The CICE default (CCSM3) radiation scheme is used which has been modified to include topographic melt ponds in the same manner as described in Ridley et al. (2018). The CCSM3 radiation scheme in CICE is analogous to the JULES scheme used in the coupled model (Ridley et al., 2018) except that penetration of solar radiation into bare ice is included and, to account for internal scattering, the bare ice albedo is increased as outlined in Sect. 4.6 below.

While the ocean model is solved on the Arakawa C-grid, (Arakawa, 1966), the sea ice model is solved on the Arakawa B-grid, with the tracer points of the two grids aligned with each other. An interpolation routine is used to couple ocean and ice velocities. To avoid issues related to the difference in model grids, single point inlets were filled-in around Antarctica in all three resolutions. As in the coupled model, the ice and ocean components are combined into a single executable, avoiding the need for a coupler.

2.6 Model performance

The GO6 models were run on the Met Office Cray XC40 supercomputing facility and the joint Met Office – NERC MONSooN collaboration service. The ORCA1 configuration with a time step of 2700 s runs one model year in 80 min on 224 cores of the XC40 with 32 of these cores dedicated to postprocessing diagnostic output using the NEMO XIOS module. The ORCA025 configuration with a time step of 1350 s runs one model year in 12 h on 486 cores of the XC40, with 6 of these cores dedicated to XIOS. The ORCA12 configuration with a time step of 300 s runs one model year in 50 h on 6237 cores of the XC40, with 72 cores dedicated to XIOS. The XIOS cores are spread over 12 depopulated nodes with only 6 cores used on each node. The NEMO code includes an option referred to as “land suppression” (Madec, 2016), which excludes much of the global land area from the calculations. For the performance figures quoted here, the land suppression option was only used for ORCA12. These figures are for integrations which output the full ocean diagnostic requirement for CMIP6 (Eyring et al., 2016).

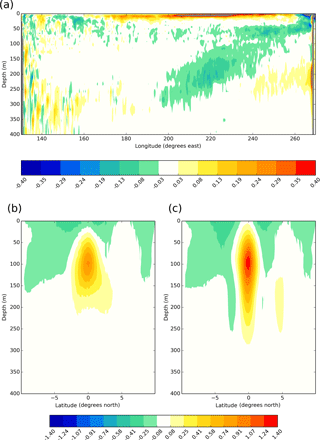
Figure 1Figure showing the impact of turning on the Hollingsworth et al. (1983) scheme for momentum advection: (a) cross section along the Equator in the Pacific of the difference between experiment and control of the diagnosed vertical tracer diffusivity (m² s⁻¹) from the TKE scheme; (b, c) cross sections of zonal velocity (m s⁻¹) at 136^∘ W in the Pacific, (b) without Hollingsworth, (c) with Hollingsworth. Model fields are 5-year means from the second 5 years of a 10-year spin-up.

Download

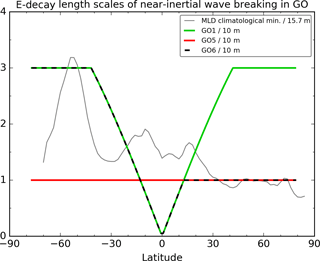
Figure 2Figure showing the variation in the nn_htau length scale with latitude for different GO configurations. This length scale controls the depth of the additional near-surface mixing added by the Rodgers et al. (2014) parameterization as described in Sect. 2.3. The length scale is normalized by 10 m. Also shown as a grey line is the zonal-mean monthly minimum mixed layer depth from the de Boyer Montégut et al. (2004) climatology. This has been normalized by 15.7 m.

Download

4.1 NEMO version upgrade and nonlinear free surface

The version of the NEMO base code has been upgraded from NEMO 3.4 to NEMO 3.6 which was released in 2015. Among the new features available for NEMO 3.6 (compared to 3.4) are the Hollingsworth et al. (1983) formulation for momentum advection, the Lagrangian icebergs scheme and the ability to simulate the circulation beneath ice shelves. The first two of these are activated in GO6 and are discussed in Sects. 4.2 and 4.5. Testing of the under-ice-shelf functionality is described in Sect. 7.

GO5 employed a linear free surface in which the volume of the ocean remains constant and the surface fresh water flux is represented as a virtual salt flux (Roullet and Madec, 2000). For GO6 we switch to the nonlinear free surface in which the volume of the ocean grid cells throughout the water column is allowed to vary with time (the z^* coordinate of Adcroft and Campin, 2004). This has the advantage that the fresh water flux at the surface can be represented accurately. It is also a prerequisite for the future inclusion of tides in the global model.

Both the upgrade to the base code version and the switch to the nonlinear free surface have been tested in separate sensitivity experiments and have been shown to have small impacts on the large-scale simulated climate (not shown).

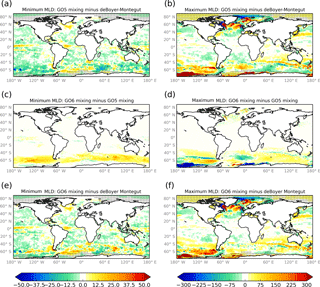
Figure 3Results from a sensitivity study where the nn_htau length scale was tuned (see Sect. 4.3). A mean monthly climatology of the mixed layer depth field in metres was calculated for the third decade of the spin-up (1996–2005). The point-wise minimum and maximum monthly values have then been calculated and plotted as anomalies against the same quantities from the de Boyer Montégut et al. (2004) climatology and as difference fields between the GO5 and GO6 mixing choices. Hashed regions indicate the presence of sea ice at any time during the year.

Download

4.2 Improved formulation of momentum advection

Hollingsworth et al. (1983) describe a computational symmetric instability associated with the vector-invariant form of the momentum equations due to Arakawa and Lamb (1981). They also provide a modified formulation for the kinetic energy divergence term which prevents the instability arising. This formulation is available in NEMO from version 3.6 and has been selected in the GO6 configuration. Ducousso et al. (2017) tested the new formulation in ORCA025 and found impacts in the most active regions of the model. In particular they found that the new formulation produced a more realistic representation of the equatorial current system in the east Pacific with a stronger and better-defined equatorial undercurrent and increased eddy kinetic energy.

Sensitivity experiments with the GO6 configuration have shown results that are consistent with Ducousso et al. (2017). Figure 1a shows the impact of turning on the Hollingsworth et al. (1983) formulation on the time-mean vertical diffusivity from the TKE scheme. Particularly noticeable is a reduction in the vertical mixing in the thermocline between about 100 and 300 m in the eastern Pacific. (There is also a reduction in the subsurface mixing in the equatorial Indian Ocean – not shown.) The reduction in mixing results in an increase in the strength of the equatorial undercurrent as shown in Fig. 1b and c, which show cross sections of the zonal currents at 136^∘ W. The equatorial undercurrent (EUC) is substantially stronger in the integration with the Hollingsworth et al. formulation and extends deeper to 250 m. Comparison with the in situ cruise data presented in Fig. 1 of Wang (2005) shows that the shape and vertical extent of the EUC with the new formulation appears to be a better match to observations, although the jet is now too strong (1.3 m s⁻¹ as opposed to about 0.9 m s⁻¹ in the observations).

4.3 Tuning of near-surface mixing

In GO5 a number of parameters that control vertical mixing were adjusted, based on the sensitivity studies of Calvert and Siddorn (2013). The most significant tuning was to the ad hoc parameterization of near-inertial wave breaking of Rodgers et al. (2014). The e-folding length scale nn_htau, associated with this parameterization can be varied with latitude. In GO5, nn_htau was reduced at mid- and high-latitudes, which reduced over-deep summertime mixed layer biases and cold sea surface temperature (SST) biases. However, the summertime mixed layers in the Southern Ocean were then too shallow compared to climatology (see Fig. 2 of Megann et al., 2014).

Figure 2 shows the choices for the latitudinal dependence of the nn_htau parameter at GO1, GO5 and GO6. Also plotted is the zonal-mean minimum monthly mixed layer depth based on the de Boyer Montégut et al. (2004) climatology. The climatology shows that the summertime mixed layers are on average deeper in the Southern Ocean than in northern mid-latitudes. Based on this and the GO5 results, the nn_htau parameter has been further tuned in GO6 to be deeper in the Southern Hemisphere. The results of a sensitivity experiment comparing the GO5 and GO6 vertical mixing tunings are shown in Fig. 3. The summertime mixed layer depths in the Southern Hemisphere have deepened compared to GO5 and are now a better match for the de Boyer Montégut et al. (2004) climatology. This reduces a summertime warm bias in the SST (not shown) which then has a major impact on the sea ice (see Fig. 4b), increasing the total volume of sea ice in the Southern Ocean year-round. The increase in the volume of sea ice is substantial, particularly in the austral winter, and is partly due to the suppression of open ocean polynyas in the Weddell Sea. The suppression of the polynyas then shallows the winter time mixed layer depths under the ice as is evident in Fig. 3d.

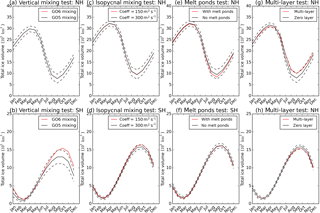
Figure 4Plots showing the mean seasonal cycle of integrated sea volume in Northern (NH) and Southern (SH) hemispheres for four sensitivity experiments: (a, b) tuning of near-surface vertical mixing; (c, d) tuning of isopycnal mixing coefficient; (e, f) introduction of explicit calculation of the impact of melt ponds on albedo versus a simple temperature-dependent albedo; (g, h) introduction of multi-layer thermodynamics versus zero-layer thermodynamics. In all cases the results with the GO6 settings are in red and with the GO5 settings in black. The dashed lines show the standard deviation of the annual mean values for the control integration in each case.

Download

As discussed further in Sect. 8, we regard the use of the Rodgers et al. (2014) scheme as a stopgap solution to the problem of underestimated mixing processes in the model and plan to move to a more physically based parameterization of these processes in future versions of the model.

4.4 Reduced isopycnal diffusion

Met Office coupled models based on GO1 and GO5 have a long-standing warm SST bias in the Southern Ocean which has recently been substantially improved (Williams et al., 2017). This has been largely attributed to atmospheric biases, particularly in the representation of clouds. However, as part of ongoing work to reduce this bias, the isopycnal diffusion parameter in the ocean was also tuned. Isopycnal diffusion by eddies is responsible for moving heat from depth to the ocean surface (Griffies et al., 2015), especially in the Southern Ocean. So a reduction in the isopycnal diffusion parameter might be expected to cool the surface.

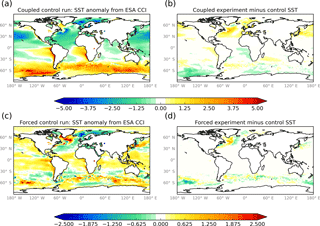
Figure 5SST anomalies and experiment-minus-control differences from sensitivity tests of halving the isopycnal diffusion parameter (from 300 to 150 m² s⁻¹) in: (a, b) the Met Office GC3 coupled configuration (Williams et al., 2017); and (c, d) the forced GO6 configuration. Anomalies are calculated against ESA CCI (Merchant et al., 2014). Model mean fields are calculated over the final 10 years of 30-year spin-up integrations. The coupled model tests used present-day climate forcing. Note the different contour scales in the coupled and forced tests.

Download

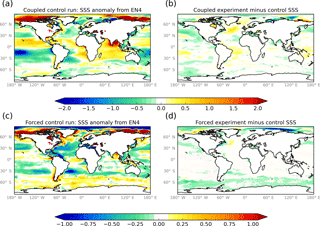
Figure 6As for Fig. 5 but for sea surface salinity (SSS, psu). Anomalies are against the EN4 analysis (Good et al., 2013). Note the different contour scales for the coupled and forced tests.

Download

Figures 5 and 6 show the results from sensitivity tests in which the isopycnal diffusion parameter has been reduced from the GO5 value of 300 m² s⁻¹ to the GO6 value of 150 m² s⁻¹. Tests were performed with the Met Office GC3.1 coupled model (Williams et al., 2017) and the forced GO6 configuration. As discussed in Sect. 8, because of the different surface boundary condition and different atmospheric forcing errors, the biases will generally be different in the coupled and forced contexts. The reduction in the isopycnal diffusion parameter cools the SST in the Southern Ocean in the coupled experiment and largely acts to reduce the warm biases there. There is a slight warming of SSTs in the Northern Hemisphere which also acts to reduce biases. In the forced test, there is some cooling of the SST in the Southern Ocean, particularly near the Ross Sea which also reduces a warm bias there. There is a dipole signature in the North Atlantic with a warming of the southern subpolar gyre and a cooling further west, which tends to exacerbate existing biases. The impact on the SSS in the coupled model is mixed, with some freshening in the Southern Ocean near the Ross Sea. In the forced model there is a more systematic freshening of the surface in the Southern Ocean which largely acts to correct a saline bias. There is also a large-scale freshening of the surface waters in the Arctic. The hydrography changes in the forced test due to the reduction of isopycnal mixing lead to a slight increase in the total volume of wintertime sea ice in the Antarctic (Fig. 4d) but do not affect the total volume of sea ice in the Arctic (Fig. 4c).

4.5 Icebergs and ice shelves

In GO5 the fresh water input from frozen land masses was represented as surface runoff close to the coastlines of Greenland and Antarctica. For Met Office coupled models prior to GC3.0 (e.g. Williams et al., 2015), the fresh water input from Antarctica was spread over a large part of the Southern Ocean south of the Antarctic Circumpolar Current (ACC) in order to crudely represent iceberg melting. In GO6 and in GC3.1, the processes involved in the input of fresh water to the ocean from frozen land masses are modelled more realistically using a Lagrangian iceberg model and a parameterization of ice shelf basal melt. Figure 7 shows the annual mean fresh water input to the ocean from Antarctica using the three methods. In the first two cases the distribution of fresh water input is fixed, but with the interactive icebergs model it will vary depending on the winds and currents.

Marsh et al. (2015) tested the iceberg module in a CORE2-forced ORCA025 integration similar to the one described in this paper. Their control integration put fresh water input as runoff near the coastline, as was done in GO5. They found that one of the main impacts of the icebergs was to suppress sea ice formation near the coast, since less fresh water is put into the ocean there, reducing stratification and warming the surface layers. With less sea ice formation there was less sea ice overall and a widespread salinification of the surface waters in the Southern Ocean due to reduced melting offshore. We find a similar impact on the sea ice fraction (Fig. 8a) and the surface salinity (Fig. 8b). Megann et al. (2014) show that compared to a climatology of the HadISST analysis (Rayner et al., 2003), the sea ice extent in GO5 was realistic in the austral winter but too low in the austral summer. Therefore a reduction in the sea ice due to the inclusion of the icebergs scheme is likely to reduce the realism of the sea ice simulation. However, the modelling of the fresh water distribution due to the icebergs is more realistic, and as discussed in Sect. 5.2, the reduction in sea ice due to the inclusion of the icebergs scheme is more than offset by the increase in sea ice due to the vertical mixing changes.

Merino et al. (2016) tested a modified version of this iceberg model in NEMO and found a freshening of the surface layers and increased sea ice due to the input of iceberg melt, in contrast to the results described here and in Marsh et al. (2015). However, their control experiment had no representation of iceberg melt water input to the ocean, whereas in our control experiment the iceberg melt water is included near to the coast which stimulates the formation of sea ice near to the coast. The reduction in sea ice (and salinification of the surface layers) that we see is due to the removal of this near-coastal freshwater input and a more realistic distribution due to the Lagrangian icebergs.

As discussed in Sect. 2.4, GO7 has open cavities under the ice shelves, whereas in GO6 the cavities are closed and fresh water is input at the edge of the ice shelves. Mathiot et al. (2017) show that the inclusion of ice shelf basal melt in a model of the Southern Ocean produces circulations on the Antarctic shelves that are absent in simulations where all the fresh water is put in at the surface. They also show that these circulations are similar in models that have the cavities open and models that close the cavities but input the fresh water through depth as in GO6. In particular, the fact that the fresh water is input at depth produces vertical mixing and, on the West Antarctic continental shelf, draws warmer, saltier water from depth to the surface resulting in a reduction in sea ice formation. In Sect. 7 we look at the impact of opening the cavities.

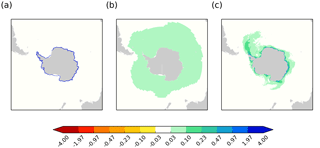
Figure 7Annual mean freshwater input (m yr⁻¹) from Antarctic land mass to ocean: (a) Annual mean freshwater input where freshwater input from Antarctica is represented as runoff close to the coastline; (b) as for (a) but with the freshwater input from Antarctica spread over the Southern Ocean to crudely represent iceberg melt; (c) annual mean freshwater input from Antarctica using the ice shelf parameterization and interactive icebergs scheme. Note the stretched colour scale.

Download

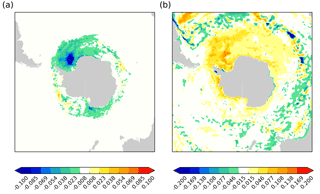
Figure 8Impact of inclusion of active icebergs scheme instead of runoff-type input used in GO5: (a) difference in sea ice fraction, icebergs minus no icebergs; (b) difference in surface salinity (psu), icebergs minus no icebergs. In both cases means are taken over the second 5 years of a 10-year spin-up.

Download

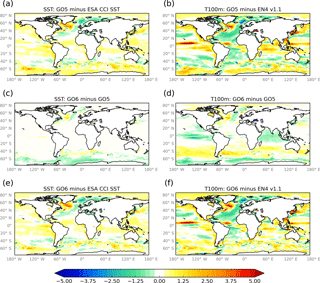
Figure 9Potential temperature (K): anomalies against climatology and GO6–GO5 differences at the surface and 100 m. SST anomalies are against ESA CCI (Merchant et al., 2014) and 100 m potential temperature anomalies are against a 20-year climatology of EN4 v1.1 (Good et al., 2013). Model fields are time-means over the third decade of the integration.

Download

4.6 Developments to the sea ice model

In parallel to the ocean model development from GO5 to GO6, the sea ice model has been developed from the GSI5.0 (Rae et al., 2015⁸) configuration used with GO5 to the GSI8.1 configuration described by Ridley et al. (2018). In assessing the GO6 ocean we therefore have to also take into account the impact of changes in the sea ice model. The two main developments in GSI8.1 compared to GSI5.0 are the replacement of the simple temperature-dependent albedo with an explicit calculation of the impact of surface melt ponds on albedo using the topographic melt pond scheme of Flocco et al. (2010), and a change to a multi-layer thermodynamics solver instead of zero-layer thermodynamics. In addition the ocean-ice drag coefficient has been nearly doubled from 0.00536 to 0.01 and, for the forced integrations, the albedo of bare ice in the visible waveband has been changed from 0.78 to 0.8333 to be more consistent with the coupled model. This albedo increase is numerically equivalent to the Semtner correction (Semtner, 1976) applied in the JULES scheme used in the coupled model (Ridley et al., 2018).

Sensitivity experiments show that the melt pond scheme reduces the volume of summertime sea ice in the Arctic (Fig. 4e), probably because it reduces the summertime ice albedo, increasing the melt rate for a given insolation. The multi-layer thermodynamics counteract this tendency by increasing the volume of summertime sea ice in the Arctic (Fig. 4g). The multi-layer thermodynamics also reduce the thickness and extent of wintertime ice in the Arctic and Antarctic (Fig. 4g and h) – a slight degradation. The multi-layer thermodynamics have nonzero thermal inertia in contrast to zero-layer thermodynamics, which increases the time taken for the ice to melt in the spring and increases the time taken for the ice to form in the autumn, since in both cases some of the heat exchange with the atmosphere is now used to change the temperature of the existing ice. In the Southern Hemisphere the changes in the sea ice volume due to the vertical mixing tuning (already discussed; Fig. 4a, b) are much larger than changes in the sea ice volume due to the changes to the sea ice model physics.

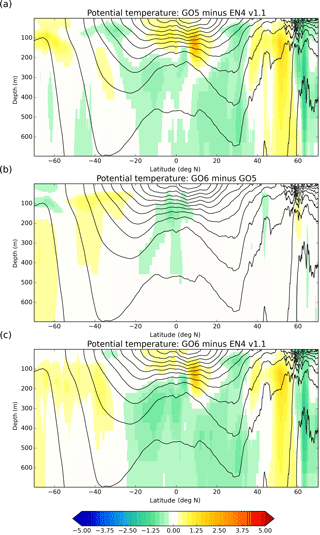
Figure 10Cross sections of zonal-mean potential temperature (K): anomalies against a 20-year climatology of EN4 v1.1 (Good et al., 2013) and GO6–GO5 differences. Line contours are zonal-mean potential density σ₀ from the GO6 integration with a contour interval of 0.5 kg m⁻³. Model fields are time-means over the third decade of the integration.

Download

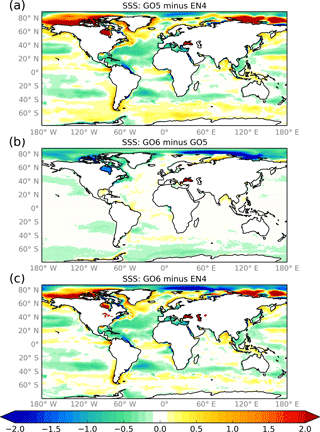
Figure 11Surface salinity (psu): anomalies against a 20-year climatology of EN4 v1.1 (Good et al., 2013) and GO6–GO5 differences. Fields are averaged over the last 10 years of the 30-year spin-up.

Download

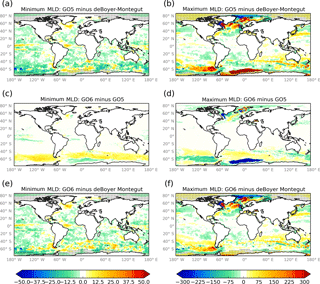
Figure 12Point-wise minimum and maximum monthly mixed layer depth (metres): anomalies against the de Boyer Montégut et al. (2004) climatology and GO6–GO5 differences. The point-wise minima and maxima are calculated as for Fig. 3. Hashed regions indicate the presence of sea ice at any time during the year.

Download

5.1 Model assessment and comparison to GO5

In this section, we evaluate the GO6-GSI8.1 $\mathrm{1}/{\mathrm{4}}^{\circ }$ configuration compared to GO5-GSI5.0, based on 30-year CORE2-forced integrations from 1976 to 2005. Time averaged fields are taken from the third decade of the 30-year integrations. These integrations are shorter than the standard CORE2 protocol specification (Griffies et al., 2009) and would be insufficient to make a full assessment of the long-term behaviour of GO6. However, here we focus on the impact of the model developments between GO5 and GO6 on the upper ocean, which equilibrates on shorter timescales. Assessment of GO6 in the full CORE2 protocol and comparison with other models is planned as future work.

Looking first at the temperature, the GO5 model is generally too warm in the Southern Ocean, in the northern subpolar gyres and in the tropics, with cold biases in the subtropical gyres (Fig. 9a, b). The changes in GO6 tend to cool the Southern Ocean south of the ACC and warm the ocean north of the ACC. There is a subsurface cooling in the tropics and a dipole pattern of warming and cooling in the North Atlantic subpolar gyre (Fig. 9c, d). With the exception of the North Atlantic subpolar gyre, the differences generally improve the model (Fig. 9e, f; compare a, b). These near-surface biases are visible in the zonal-mean cross section of temperature (Fig. 10). There are also deeper cold biases in the tropics and subtropics. The GO6 changes cool the near-surface ocean south of the ACC and warm it north of the ACC, reducing corresponding cold and warm biases in the top 100 m. There is a warming of the Southern Ocean below 200 m which introduces a slight warm bias in GO6. The tropical ocean is cooled in the near-surface layers, which reduces the near-surface warm bias but to some extent also exacerbates the deeper cool bias.

Regarding surface salinity biases, the GO5 model tends to be too salty in the Southern Ocean, in the subpolar gyres and on the continental shelf in the Arctic, and too fresh in the central Arctic Ocean and in the subtropical gyres (Fig. 11). The main impact of the GO6 changes is at high latitudes. The Southern Ocean tends to freshen south of the ACC which reduces the large-scale saline bias. There is a general freshening of the surface layers in the Arctic going from GO5 to GO6 which worsens the fresh bias in the central Arctic Ocean but mitigates some of the salty biases near to Siberia and Canada.

Summertime mixed layer depths tend to be too shallow in the Southern Ocean in GO5 and this bias tends to be corrected in GO6 (Fig. 12a, c, e). The wintertime mixing in GO5 is too deep in the Atlantic subpolar gyre and the Greenland–Iceland–Norway seas and also in the Southern Ocean west of the Drake Passage and in the Weddell Sea. The very deep wintertime mixed layers in the Southern Ocean are much reduced in GO6 (Fig. 12b, d, f). The deep mixing in GO5 in the Weddell Sea is related to the presence of a large open-ocean polynya which will be discussed in Sect. 5.2.

Figure 13 shows the mean seasonal cycle of integrated sea ice extent and volume in the Northern and Southern hemispheres. In the Arctic, GO5-GSI5 and GO6-GSI8.1 both do a reasonable job of simulating the total wintertime sea ice extent compared to a climatology of the HadISST analysis (Rayner et al., 2003), but both models have a too small extent in the boreal summer. The total volume is underestimated compared to the Pan-Arctic Ice Ocean Modeling and Assimilation System (PIOMAS; Zhang and Rothrock, 2003) reanalysis year-round, but especially in the boreal summer. By this metric there is a relatively small difference between the two model versions in the Arctic, mostly to do with the timing of the seasonal cycle. There is a slightly faster springtime melting and slightly faster ice formation in the autumn in GO6-GSI8.1 compared to GO5-GSI5.0 but the minimum and maximum ice volumes are unchanged. In the Antarctic, the wintertime sea ice extent is reasonable compared to HadISST but there is a large underestimation of the summertime extent in both configurations. The wintertime total volume is greatly increased in GO6-GSI8.1, which is partly owing to the fact that the open-ocean Weddell Sea polynyas seen in the GO5-GSI5.0 simulations do not appear in the GO6-GSI8.1 simulations.

To look in more detail at the spatial differences between the GO5-GSI5.0 and GO6-GSI8.1 runs, mean seasonal sea ice concentration fields (Fig. 14) and sea ice thickness fields (Fig. 15) have been analysed. The analysis shows that GO6-GSI8.1 has improved simulations of sea ice concentration in winter in both the Arctic and the Antarctic. In the Arctic, the concentration is reduced in the Greenland and Barents seas, mitigating positive biases against HadISST. In the Antarctic, there is a general increase in sea ice concentration everywhere, most markedly in the Bellingshausen–Amundsen and Ross seas and in the central Weddell Sea. In these areas, biases against HadISST have been reduced, but the bias is increased west and north of the Antarctic Peninsula (Fig. 14a–e and f–j). In the boreal summer, sea ice concentration over most of the Arctic has slightly reduced in GO6-GSI8.1, a degradation compared to HadISST. In the Antarctic, summertime sea ice concentration tends to increase in GO6-GSI8.1 closer to the coast but reduce further offshore. For the most part, this reduces biases compared to HadISST, except for the eastern Weddell Sea and the Pacific sector of the Southern Ocean, where the bias has increased (Fig. 14p–t).

Figure 15 shows spatial sea ice thickness distribution in GO6 and difference between GO6 and GO5. There is a moderate increase in the Arctic ice thickness in the boreal winter and moderate decrease in the boreal summer in GO6 (Fig. 14b, d). Comparison with Fig. 13 shows that this is mainly due to the small change in the timing of the seasonal cycle already noted. In the Antarctic, GO6 has large thickness increases all-year round compared to GO5, with the main increase in thicknesses in the western Weddell and Ross seas (Fig. 14f, h).

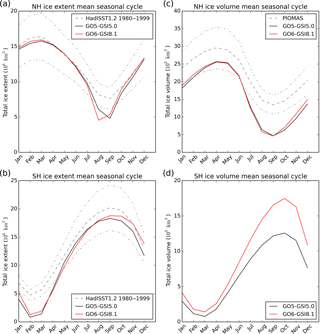
Figure 13Mean seasonal cycles for integrated sea ice extent and volume for the two hemispheres (NH and SH) for GO5-GSI5 and GO6-GSI8.1. Sea ice extent is calculated as the integral of the area of grid cells where the sea ice concentration is greater than 15 %. The meaning period is 1977–2004. Grey dashed lines in the extent plots show a climatology (mean and ±20 %) of the HadISST analysis (Rayner et al., 2003) Grey dashed lines in the Northern Hemisphere volume plot show a climatology (mean and ±20 %) of the PIOMAS (Zhang and Rothrock, 2003) reanalysis.

Download

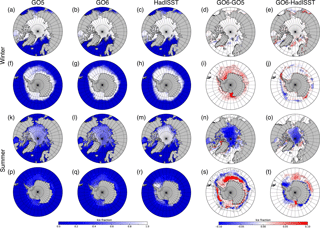
Figure 14Seasonal-mean multi-annual sea ice concentration for summer and winter, averaged for 1978–2005 in GO5-GSI5.0, GO6-GSI8.1 and the HadISST analysis (Rayner et al., 2003). Panels (a)–(e) show GO5-GSI5.0, GO6-GSI8.1 and HadISST ice concentration and the concentration difference between GO6-GSI8.1 and GO5-GSI5.0 and the bias between GO6-GSI8.1 and HadISST respectively for DJF in the Northern Hemisphere (NH); (f)–(j) are the same as above but for JJA in the Southern Hemisphere (SH); (k)–(o) are the same as (a)–(e) but for JJA in the NH; (p)–(t) are the same as (f)–(j) but for DJF in the SH.

Download

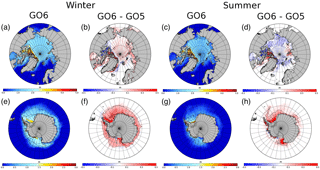
Figure 15Seasonal-mean multi-annual sea ice thickness (m) in the summer and winter, averaged for 1978–2005 in GO6-GSI8.1, GO5-GSI5.0 and the differences between the two runs. Panels (a)–(d) show sea ice thickness in GO6-GSI8.1 and the difference between GO6-GSI8.1 and GO5-GSI5.0 for DJF (a, b) and JJA (c, d) in the Northern Hemisphere (NH); (e)–(h) are the same as above but for JJA (e, f) and (DJF) (g, h) in the Southern Hemisphere (SH).

Download

5.2 Attribution of changes in results to model changes

In this section, we summarize the sensitivities described in Sect. 4 and show which model changes are responsible for the main changes between GO5 and GO6.

The simulation of the sea ice is an important aspect of the Southern Ocean, feeding back on the ocean hydrography. As shown in Figs. 13, 14 and 15 there is substantially more sea ice in the Southern Ocean in the GO6 simulation compared to GO5. The concentration and the thickness are increased in most areas, especially in the austral winter. Part of this difference arises in the Weddell Sea where, in the GO5 simulations, large open-ocean polynyas tended to open up in the winter (Megann et al., 2014). For GO6 the polynyas tend to be suppressed. Sensitivity experiments show that the change likely to be mainly responsible for the increased sea ice is the vertical mixing change described in Sect. 4.3. This deepens the summertime mixed layers in the Southern Ocean and reduces the surface warm bias (see Figs. 12 and 9), allowing more sea ice to persist through the austral summer and maintaining the stratification which in turn is favourable for sea ice formation in the following winter. Most of the other GO6 changes tend to suppress sea ice formation in the Southern Ocean. The Lagrangian icebergs scheme moves fresh water offshore resulting in saltier and less stable near-shore water. The ice shelf melting parameterization puts fresh water into the ocean at depth, destabilizing the water column and helping to bring warmer, saltier water to the surface. Both of these changes will therefore tend to suppress sea ice formation near the coast and the ice shelf edges and have been shown to result in less sea ice in sensitivity studies (Marsh et al., 2015; Mathiot et al., 2017). The developments to the sea ice model have a small impact on the integrated sea ice area and volume in the Southern Ocean (Fig. 4); the use of multi-layer thermodynamics tends to slightly reduce the volume of Southern Ocean ice in the austral winter. It is therefore apparent that in this aspect the vertical mixing change dominates the other changes and results in an improved sea ice simulation. This result is consistent with the results presented by Heuzé et al. (2015) and Kjellsson et al. (2015) who also show that increased near-surface vertical mixing in the Southern Ocean tends to close open-ocean Weddell Sea polynyas.

The increased Southern Ocean sea ice for GO6 is driven by reduced melting in the open ocean in response to colder summertime SSTs. The reduced sea ice melt should in turn result in a salinification of the near-surface layers in the Southern Ocean due to reduced fresh water input. However, Fig. 11 shows that going from GO5 to GO6 there is a net freshening of near-surface waters in the Southern Ocean, which extends to about 150 m depth (not shown). This corrects a saline bias compared to EN4. One possible mechanism for this could be the introduction of Lagrangian icebergs which move fresh water offshore, but as discussed in Sect. 4.5 the net effect of the icebergs is actually to indirectly make the surface layers more saline by reducing the production of sea ice and hence reducing the total overall sea ice (Fig. 8a). The actual cause of the freshening at GO6 appears to be the reduction in the isopycnal diffusion coefficient (Fig. 6c, d), which reduces the amount of warm, salty water upwelled from depth in the Southern Ocean and counteracts the salinification due to reduced sea ice melting.

Figures 9 and 10 show that the main change in the tropics going from GO5 to GO6 is a subsurface cooling at around 100–200 m in the Indian and eastern Pacific oceans. This mitigates a subsurface warm bias visible at about 100 m in the GO5 results, but also in the Pacific slightly exacerbates a deeper cold bias. Sensitivity experiments (not shown) suggest that the primary change responsible for this cooling is the use of the Hollingsworth et al. (1983) formulation of the momentum advection scheme. As described in Sect. 4.2, the subsurface mixing in the central Indian Ocean and eastern Pacific Ocean is reduced when the Hollingsworth et al. formulation is used. It seems likely that this is causing less heat to be mixed down, giving a cooling of the subsurface layers, which for the most part reduces existing subsurface biases in the tropics. One might expect that if less heat were being mixed down then the SST would show a warming signal. However, in these forced experiments the SST is quite strongly constrained by the forcing and the ocean “sees” an atmosphere with effectively infinite heat capacity.

The main hydrography changes in the Northern Hemisphere between GO5 and GO6 are changes to the temperature and salinity patterns in the North Atlantic subpolar gyre and a general freshening of the near-surface waters in the Arctic (Figs. 9 and 11). Comparison of these figures with Figs. 5d and 6d shows that the reduction of the isopycnal mixing coefficient is likely to be the biggest cause of both of these changes. The sensitivity experiment shows that while the reduction of the isopycnal mixing coefficient gives a freshening of surface waters in the Arctic, this does not seem to impact significantly on the sea ice simulation. The changes in the sea ice simulation in the Arctic between GO5-GSI5.0 and GO6-GSI8.1 must therefore be a result of the changes in the sea ice model formulation between GSI5.0 and GSI8.1. As noted in Sect. 4.6 the improvement in the representation of melt ponds and the inclusion of multi-layer thermodynamics appear to have opposite effects in the Arctic with the melt ponds decreasing the summertime ice and the multi-layer thermodynamics increasing the summertime ice. As described in Sect. 5.1, the net effect appears to be to change the timing of the seasonal cycle slightly with faster melting in the spring and faster formation in the autumn but the minimum and maximum values unchanged (Fig. 13a and c).

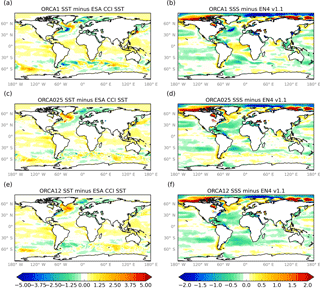
Figure 16Cross-resolution results: (a, c, e) model SST anomalies (K) against ESA CCI (Merchant et al., 2014); (b, d, f) model SSS anomalies (psu) against the EN4 v1.1 analysis (Good et al., 2013). In all cases the model fields are 10-year means for the third decade of the spin-up (1996–2005).

Download

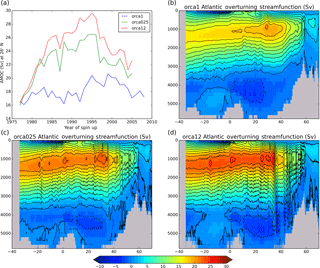
Figure 17Cross-resolution results: Atlantic overturning streamfunction. (a) Time series of annual-mean AMOC at 26^∘ N for 1976–2005; (b–d)  AMOC (Sv) averaged over the third decade of the spin-up (1996–2005). The line contours are plotted every 2 Sv.

Download

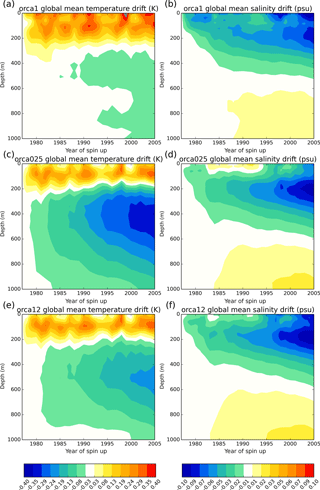
Figure 18Cross-resolution results: (a, c, e) global-mean model potential temperature drift from initial conditions (K); (b, d, f) global-mean model salinity drift from initial conditions (psu).

Download

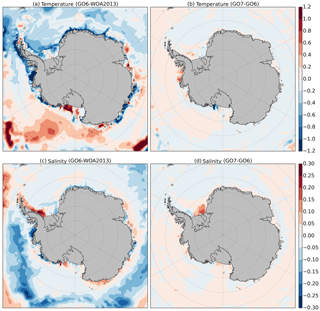
Figure 19Maps of potential temperature (K) and salinity (psu) averaged between 300 and 1000 m. (a, c) Differences between GO6 and WOA2013 (Locarnini et al., 2013; Zweng et al., 2013) data; (b, d) differences between GO7 and GO6. Grey shading represents areas covered by ice shelves or ice sheets, or with bathymetry shallower than 300 m.

Download