the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Accelerating simulations using REDCHEM_v0.0 for atmospheric chemistry mechanism reduction
Zacharias Marinou Nikolaou
Jyh-Yuan Chen
Yiannis Proestos
Jos Lelieveld
Rolf Sander
Chemical mechanism reduction is common practice in combustion research for accelerating numerical simulations; however, there have been limited applications of this practice in atmospheric chemistry. In this study, we employ a powerful reduction method in order to produce a skeletal mechanism of an atmospheric chemistry code that is commonly used in air quality and climate modelling. The skeletal mechanism is developed using input data from a model scenario. Its performance is then evaluated both a priori against the model scenario results and a posteriori by implementing the skeletal mechanism in a chemistry transport model, namely the Weather Research and Forecasting code with Chemistry. Preliminary results, indicate a substantial increase in computational speed-up for both cases, with a minimal loss of accuracy with regards to the simulated spatio-temporal mixing ratio of the target species, which was selected to be ozone.
- Article
(8181 KB) -
Supplement
(116 KB) - BibTeX
- EndNote
Atmospheric chemical mechanisms, which are typically used in air quality research and forecasting codes, generally contain a large number of species and reactions. This poses a significant computational workload, which in some cases may account for more than 80 % of the total simulation time (Dunker, 1986), even with the advent of modern hybrid computer architectures (Christou et al., 2016). These mechanisms describe an important set of processes in the troposphere; for example, the degradation of volatile organic compounds (VOCs) and the formation of ozone (O3), the latter being a major oxidant and pollutant. As a result, mechanisms with varying levels of complexity are included in regional and global atmospheric chemistry codes, the overall performance of which strongly depends on the choice of chemical mechanism.
Apart from the large number of species that require solving at every point in the computational domain and for every time step, there is a large disparity in the chemical timescales of the interacting species (Sandu et al., 1997b). This results in a stiff system of non-linear equations for the reaction rates, which is computationally expensive to integrate, and adds to the computational cost (Sandu et al., 1997a). Similar issues are encountered in the field of combustion research: detailed mechanisms describing the combustion of a fuel contain hundreds of species and thousands of reactions. However, from a practical point of view, one is usually only interested in a handful of important variables – in combustion this includes quantities such as ignition delay time, laminar flame speed etc., while in atmospheric chemistry this includes ozone∕NOx mixing ratios and so on. In both cases, the sensitivity of quantities of interest to certain species and reactions, can be minor in relation to dominant species and reactions. As a result, solving for all species in the detailed chemical mechanism might not actually be required in order to obtain accurate estimates of the target quantities. To this end, chemistry reduction techniques have been developed to reduce the dimensionality of the problem. In turn, this results in a reduction of the computational requirements associated with detailed-chemistry simulations and an acceleration of the simulation. Even though this is common practice in combustion research using a variety of methods (Lam and Goussis, 1988; Lu and Law, 2005; Mass and Pope, 1992; Niemeyer and Sung, 2011; Nikolaou et al., 2013, 2014; Pepiot-Desjardins and Pitsch, 2008; Peters and Rogg, 1993; Pope, 1997; Tomlin et al., 1997; Turanyi et al., 1989), chemistry reduction methods have seen limited use in atmospheric chemistry applications.
The usual reduction process of a detailed chemical mechanism begins with the identification of an accurate “skeletal” mechanism. The “skeletal” mechanism is a subset of the detailed mechanism, and is generated by eliminating unimportant species and reactions from the detailed mechanism for the problem at hand. Further reduction of the skeletal mechanism is also possible. This can be achieved by a variety of timescale analysis methods, which are applied to the skeletal mechanism, such as quasi-steady-state assumption (QSSA), computational singular perturbation (CSP) (Lam and Goussis, 1988), intrinsic low dimensional manifolds (ILDM) (Mass and Pope, 1992) etc. Timescale methods are employed for finding species which are approximately in steady state. Following this, a non-linear system of equations is solved for the steady-state species mixing ratios. As a result, timescale analysis methods are most efficient when applied to relatively small skeletal mechanisms rather than the full detailed mechanism. An approach such as this, using CSP, was utilized by Neophytou et al. (2004) in order to construct a reduced mechanism for the Carbon Bond mechanism (CBMIV) (Gerry et al., 1989). In this study, our interest is in generating skeletal mechanisms, which is the first step in the reduction process, and can be used as a starting point for further reduction, in addition to being applied to more comprehensive chemistry codes.
Sensitivity analysis (SA) is perhaps the oldest and most straightforward of methods for identifying skeletal mechanisms (Turanyi et al., 1989). In SA, suitable sensitivity coefficients are defined which are usually reaction-based. The sensitivity of a species in each reaction is calculated for a particular configuration (reaction mode), and reactions that have sensitivity coefficients below a threshold value are identified as redundant and are removed from the detailed mechanism. An approach such as this was employed by Heard et al. (1998) to reduce the CBM-EX tropospheric chemical mechanism. The SA resulted in the elimination of a number of reactions from the detailed mechanism, and following steady-state assumptions this approach was further introduced to derive a reduced and computationally faster mechanism. A sensitivity analysis assisted tabulation method was also used by Dunker (1986) for accelerating the species integration. Furthermore, SA was employed by Whitehouse et al. (2004) as a first reduction step for generating a skeletal mechanism from the Master Chemical Mechanism (MCM) (Derwent et al., 1998). Reaction-based approaches such as sensitivity analysis and principal component analysis (PCA) (Turanyi et al., 1989), result in the removal of reactions from the detailed mechanism, but may not always significantly reduce the number of species which is the key factor controlling computational time in numerical simulations. To this end, a number of other techniques have been developed which are species-oriented rather than reaction-oriented. Species lumping is a popular approach in which a number of reacting species are combined into surrogate species; the net effect of these species on the system evolution remains approximately the same. Lumping has been used in the development of the Regional Acid Deposition Model (RADM2) (Stockwell et al., 1990), in the development of SAPRC (Carter, 2000), and for condensing the MCM (Whitehouse et al., 2004). Jenkin et al. (2008) also used lumping for developing the Common Representatives Intermediates (CRI) mechanism from the MCM. Direct relation graph (DRG), is an alternative and efficient species-based method for the generation of skeletal mechanisms, originally proposed by Lu and Law (2005). In DRG, a suitable species direct interaction coefficient (DIC) is defined. The DIC measures the importance a particular species has on a predefined set of target species. DRG eventually results in the removal of species, in contrast with classic reaction-based SA. In the original version of the DRG method, the target species set only included species appearing in the same reaction as the target species. However, species not interacting directly with the target species through a reaction, may still be indirectly important for a target species of interest. Therefore, an extension of the DRG method, namely DRG with Error Propagation (DRGEP) was proposed to address this issue (Niemeyer and Sung, 2011; Pepiot-Desjardins and Pitsch, 2008). In DRGEP, the DIC is defined so that the effect of the reaction path is also taken into account during the reduction process. DRGEP has been extensively used to generate skeletal mechanisms for combustion applications, with good overall results, and many variants of the method have subsequently been developed using different DIC definitions and route-finding algorithms (Chen and Chen, 2016; Niemeyer et al., 2010; Stagni et al., 2016). DRGEP has been successfully used by Xia et al. (2009), in combination with a number of other methods, to reduce the a-pinene oxidation subset of the MCM.
In comparison to SA, and lumping methods, DRGEP has seen limited use for reducing complex atmospheric chemical mechanisms, despite its large potential. In addition, the majority of studies in the literature (which used SA) focus on generating subsets of very detailed chemical mechanisms such as the MCM. As a result, the skeletal mechanisms generated from MCM are still of a prohibitive size for efficient forecasting purposes (Whitehouse et al., 2004). Conversely, our focus in this study is on chemical mechanisms that are commonly used in atmospheric models. These mechanisms are already condensed mechanisms, which have typically been developed using a bottom-up approach, and include a large number of surrogate/lumped species. Thus, it is instructive to investigate whether DRGEP can be used for further reduction of these already condensed mechanisms, as a first step in the reduction process.
Another important point to note is that the majority of studies in the literature have only focused on a priori evaluation of the skeletal chemical mechanisms: their performance was only evaluated against the model scenario results, which usually involved 0-D box model simulations. However, in a practical air-quality forecast simulation, advection, diffusion, and the more refined calculation of photolysis rates, all affect the spatio-temporal concentration of the species. These effects, among others, lead to different mixing ratios in regions that have NOx-limited conditions compared with regions that have NOx-saturated conditions. This affects the species production/destruction rates and reduction process, and to date, at least to the knowledge of the authors, no a posteriori validation has been conducted using actual forecasting simulations.
In this study, DRGEP is employed in order to examine whether sufficiently accurate skeletal mechanisms can be generated for a detailed mechanism which is commonly used in forecasting codes, namely the Regional Atmospheric Chemistry Mechanism (RACM). This is an updated version of the Regional Acid Deposition Model (RADM2) mechanism by Stockwell et al. (1997a), and describes the degradation of a number of VOCs. It is a condensed chemical mechanism but it is relatively large, including 75 species and 237 reactions; therefore, it is a good candidate for reduction using DRGEP. The focus in particular, is on developing skeletal chemistry for application to ground-level ozone prediction in relatively polluted areas.
In the text which follows, Sect. 2 introduces the DRGEP method, and Sect. 3 lists the process for generating the skeletal mechanism as well as the a priori validation. Details of the a posteriori validation using a popular weather research and forecasting code are given in Sect. 4.
Direct relation graph (DRG) is a method for generating subsets of detailed chemical mechanisms by removing species that have a negligible effect on a predefined set of target species. In the original version of the DRG method developed by Lu and Law (2005), the DIC rT,B between a target species T and a non-target species B is defined as
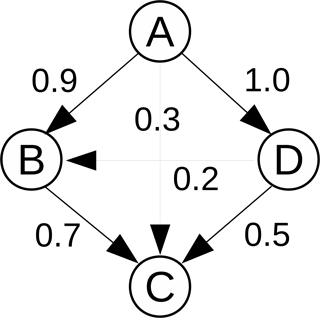
where is the net rate of species T from reaction i, and δi,B is an index specifying the existence of B in reaction i. The net rate of a species from a general reversible reaction is calculated using , where νi,T is the difference in the stoichiometric coefficients of species T in reaction i, and is the net rate of reaction i. The index δi,B is equal to 1 if B exists in reaction i, and 0 otherwise. Clearly, , and rT,B is generally not equal to rB,T. A large value of rT,B implies that species B is important in the evaluation of the rate of T, while a low value implies that it is not as important. A threshold (ϵ) is introduced, and provided , species B is added to the set of dependent species of T, otherwise it is deemed unimportant and removed. This relation is denoted as a direct path T→B. An example of a DRG involving four species A, B, C, and D, is given in Fig. 1 with the numbers indicating the values of the DICs for each pair. The process is repeated for all target species Ti, and the final set of species in the skeletal mechanism is constructed from the union of all target species sets. Species not included in the union set are eliminated, as are reactions involving any of the eliminated species.
DRG has been applied with good overall results in a number of studies in combustion research, yet the simple definition of the interaction coefficient in Eq. (1) has some important limitations. Consider the model situation depicted in Fig. 1. If A is the target species and C is the species in question, then with an example threshold value (ϵ) of 0.1, C would be added to the dependent set of A. However, it is clear that “stronger”, i.e., more important paths from A to C exist, for example, A → B → C. Thus, the notion of “path” becomes important, and a suitable DIC definition is required able to describe this. In addition, there are also alternative paths, e.g., A → D → C or A → D → B → C.
The DRGEP method aims to account for the above points by using an improved DIC definition and reduction strategy. In DRGEP (Niemeyer and Sung, 2011; Pepiot-Desjardins and Pitsch, 2008), the DIC is first defined using
where the production PT and consumption terms CT of T are defined as
and
The DIC, as defined above, is calculated for all species. The path interaction coefficient (PIC) for a given path p connecting target species T and B is then defined as
i.e., it is the product of all DICs along that path. The PIC is calculated for all possible paths connecting T to B, and an overall path interaction coefficient (OIC), is then calculated using
i.e., the strongest path from T to B is identified based on the product of the DICs of connected nodes across all paths linking T and B. In the example in Fig. 1, the strongest path is A → B → C. This is due to the fact that for this path , which is the largest value, and both B and C are included in the set of A. The process is repeated for all target species of interest, and species with overall interaction coefficients less than a predefined threshold value are removed.
The identification of the strongest path is a common problem in computational science, and a number of different route-finding algorithms have been developed for this task. In this study, we employ a classic algorithm for searching through the connected nodes and obtaining , which equates to the “strongest” path (Dijkstra, 1959). An in-house code, namely REDCHEM_ v0.0 was specifically developed for the DRGEP method, and for all associated functions including the route-finding subroutines.
Reduction methods require input data, and these data should be representative of the actual reaction scenario. This translates to using actual weather-forecast simulation data as input for the DRGEP method. However, this is hardly ever done in practice, as there is a large computational overload for conducting these kinds of simulations in the first place. As a result, a computationally more efficient initial-value problem (box model) is used as a model scenario for the reduction, which is common practice in chemical mechanism reduction studies (Dunker, 1986; Heard et al., 1998; Neophytou et al., 2004). The species mixing ratios Ci evolve according to
where Gi are non-linear functions of the species rates, with initial conditions for the species mixing ratios, and T0 for temperature. The pressure is kept fixed at 1.0 atm, and the temperature at 298.0 K. The kinetic pre-processor library (KPP) (Daescu et al., 2003; Damian et al., 2002; Sandu et al., 2003) is used for the numerical integration of Eq. (7). The KPP library includes a number of different solvers, and in this study a 5-stage Runge–Kutta method (Hairer and Wanner, 1993; Hairer et al., 1993) was used from the package (Radau5). This method is stiffly accurate and robust, and is often used for benchmarking purposes.
Table 1Initial species mixing ratios (ppbv) for RACM as deduced from Heard et al. (1998). Water content is 107 ppbv, CO content is 2310 ppbv. Pressure is fixed at 1 atm, and temperature at 298 K. VOC∕NOx ratios (methane not included) for cases A–F are 4.2, 10.7, 19.1, 4.4, 11.1, and 19.8.
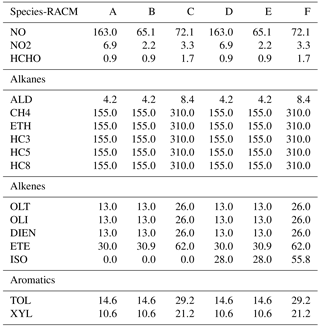
Six different initial scenarios are considered. The species mixing ratios for each model scenario are given in Table 1. These model scenarios were used by Heard et al. (1998) for reducing the CBMEX mechanism using sensitivity analysis. In this work, the same mixing ratios are used as per Table 1 of Heard et al. (1998), but are adapted for the chemical mechanism used in this study. In this paper we group important alkane, alkene, and aromatic species for each mechanism, and initialize their mixing ratios based on the relevant alkane, alkene, and aromatic species found in the study of Heard et al. (1998). Cases A–C correspond to increasing VOC∕NOx ratios not including isoprene, while cases D–F correspond to about the same VOC∕NOx ratios with isoprene included. The VOC∕NOx ratios are relatively high, and this ensures that a large number of VOC-relevant reactions are activated; thus, in this process a relatively large region of the composition space is covered. At the same time we are interested in ozone production in relatively highly polluted areas where such conditions are typically found.
The J values for the photolysis rate coefficients are based on parameterizations as developed in the MCM (Derwent et al., 1998). These are given by
where θ is the solar azimuth angle, and I, M, and N are reaction-specific constants. A 48 h run is conducted for each scenario, which results in a total of 496 datasets. These scenarios are used as input for DRGEP and the reduction process is done on a dataset basis. Important species are retained for each dataset, and the process is repeated for the next dataset. Any new species not already included in the dataset is added. Once all datasets are considered, a species union set is formed, and any reactions involving species other than those included in the species union set are removed. The target species is set to be O3, which is an important pollutant of interest. In addition, O3 is eventually produced by the degradation of the VOCs through a large number of reaction pathways; therefore, it is a good target for the reduction.
Table 2Overall interaction coefficients (OICs) for target O3 (top 35) for case A at t=12 and t=24 h.
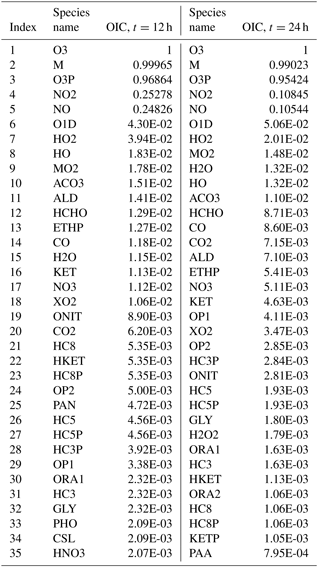
As an example, Table 2 lists the OIC values for target O3 as obtained for scenario A at midday (t=12 h) and midnight (t=24 h). Clearly, there is a difference in the OIC values for each species since the rate constants depend on the solar azimuth angle which determines the rate constants of the photolytic reactions. Top scoring species for O3 include third-body species M, and oxygen species such as O3P (ground-state oxygen atom) and O1D (excited state oxygen atom). This is expected since these species readily react to produce O3 through the reactions and . Nitrogen oxides NO and NO2 also score high as they too react both directly and indirectly with ozone. Direct paths include the reactions and , while indirect paths include reactions with O3P. The methyl peroxy radical MO2 ranks high as it is involved in numerous reactions with VOCs. The hydroxyl radical HO also scores high since it is the main oxidation path of the VOCs which eventually end up producing ozone. With a threshold of (which results in a 54-species subset as explained later in the text), 18 species will be included in the set for t=12 h, and 11 species will be included for t=24 h. The process is then repeated for all other datasets to form the overall species union set for the target O3.
In order to quantify the quality of the skeletal mechanisms generated using DRGEP, a percentage error is defined based on the target species of interest, i.e., ozone. For a mixing ratio obtained using the skeletal mechanism , and a mixing ratio using the detailed mechanism , this is defined as
where N is the total number of cases. Note that zero values are not taken into account for the error calculation.
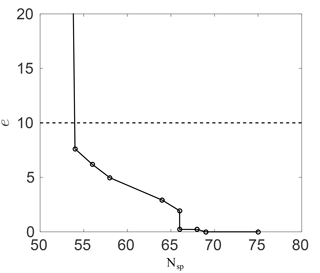
Figure 2Ozone mixing ratio percentage error against the number of species in the skeletal RACM mechanism.
Figure 2 shows this error against the number of species in the skeletal mechanism. As expected, the error increases as more species are removed. With about 10 species removed (75 to 65) the error is negligibly small. The error then increases once more than about 10 species are removed; however, the error remains small down to about 55 species (20 species removed) at less than 10 %. The huge spike in the error below about 55 species results from the removal of important intermediates.
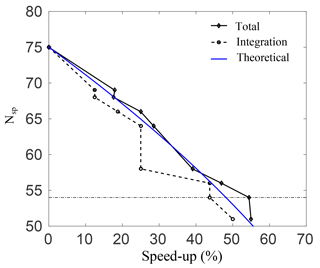
Figure 3Number of species plotted against the percentage speed-up for the total simulation time, and for integrating Eq. (7) alone.
Figure 3 shows the percentage speed-up (CPU time) gained, against the number of species in the skeletal mechanisms. This is done for case A, and similar results were observed for the rest of the cases. The speed-up is calculated for both the total simulation time, and for integrating Eq. (3) alone. The threshold line where the error in O3 prediction spikes as per the results in Fig. 2 is also shown. Clearly, as the number of species is reduced, the computational time drops and there is an increase in both speed-ups. It is interesting to note that for a decrease from 64 to 58 species there is no increase in integration speed-up. This implies that the stiffness of the remaining species and equations is unchanged. Nevertheless, there is an increase in the total speed-up of almost 10 % for a decrease from 64 to 58 species, which is due to simulation overheads alone and is quite significant. The average speed-up due to overhead computations is found to be 6.6 %. At the threshold error (e) of 10 %, the smallest possible skeletal mechanism contains 54 species and 150 reactions (the threshold for OIC at this point is ), which is significantly smaller than the detailed mechanism.
For this mechanism, the total speed-ups and integration speed-ups are 54.4 % and 43.7 %, respectively. In general, the CPU time scales with the total number of species in the system due to the evaluation of the Jacobian when dealing with stiff systems. For integration of the system alone, the expected speed-up percentage scales as speed-up , and this is shown as a blue line in Fig. 3. Clearly, there is a good qualitative agreement with the theoretical result.
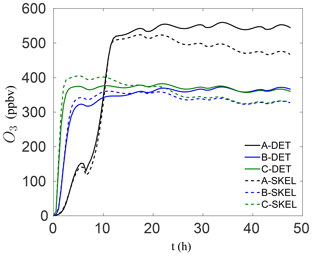
In order to visualize the errors in the ozone mixing ratio more clearly, Fig. 4 shows the solution profiles for scenarios A–C for the 48 h simulations, using the detailed and worst performing skeletal mechanism (which has 54 species). It is clear that the agreement with the detailed mechanism is very good for all six scenarios. In the isoprene scenarios D–F, similarly good results were obtained, although these results are not presented here. It is also important to note that the agreement is particularly good both early in the simulation and at later times for the box model problem. In a forecasting simulation, the situation is somewhat different. Typical time steps used in forecasting simulations are of the order of minutes, and a new initial-value problem is solved at every time step for the species mixing ratios, using the previous time step mixing ratios as the new initial condition. Furthermore, an operator splitting approach is used in the majority of codes for integrating the species mixing ratios, and this process is equivalent to filtering/smoothing the mixing ratio fields, which reduces the stiffness of the system. From this point of view, integration in forecasting codes is less stringent than integration in box model runs. In this sense, the skeletal mechanism need only be accurate enough over the integration time step, before the next initial-value problem is solved.
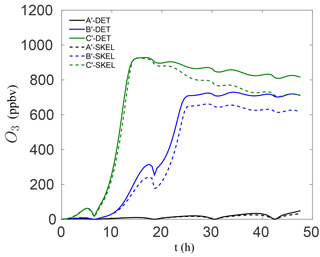
It is also important to note that the skeletal mechanism was developed with relatively polluted conditions in mind, for predicting ozone, which explains the relatively large VOC∕NOx ratios used for the reduction in Table 1. However, the method is general and can be tailored for modelling conditions of specific interest, e.g., low VOC∕NOx conditions. In order to examine the performance of the smallest skeletal mechanism for such conditions, additional box model runs were conducted for significantly lower VOC∕NOx ratios. In particular, the NO and NO2 mixing ratios in Table 1 were increased by a factor of 6 for each species, leading to initial conditions with VOC∕NOx ratios of 0.7, 1.8, and 3.2 for modified scenarios A′–C′, respectively. The results for the worst-performing skeletal mechanism (which has 54 species) are shown in Fig. 5. The agreement with the detailed chemical mechanism is particularly good for all three cases, both at early times and for longer times. Even though the chemistry for low VOC∕NOx conditions is somewhat different, the results in Fig. 5 indicate that the reduction process is not as sensitive to the VOC∕NOx ratio – the most important parameter was instead found to be variation in sunlight intensity due to the activation/deactivation of photosensitive reactions.
The results of the previous section constitute an a priori validation. In an actual simulation, the photolysis rates and the species mixing ratios due to the effects of advection, diffusion, and so on, can be substantially different from the conditions in a box model. As a result, the species rates will also differ which affects the reduction process. The aim of this section is to examine the performance of the skeletal mechanism generated in the previous section, by implementing it in an actual atmospheric-chemistry simulation, and comparing it with results using the detailed chemical mechanism.
4.1 WRF-Chem simulation set-up
The Weather Research and Forecasting system with Chemistry (WRF-Chem/version 3.9.1.1) was employed in this work. WRF-Chem, which has been jointly developed by several research institutes (https://www2.acd.ucar.edu/wrf-chem, last access: 1 March 2018), is a state-of-the art, open source, limited-area atmospheric model, featuring a highly parallelized code. WRF-Chem is used for both research applications and for operational numerical weather and air-quality predictions, and is an online, fully coupled model, which integrates and calculates meteorology, gas-phase chemistry, and aerosols simultaneously (Grell et al., 2005). WRF-Chem utilizes the Advanced Research WRF (ARW) solver (Skamarock et al., 2005), where the transformation, mixing-phase, and transport of chemical species and aerosols, are calculated following the same prognostic equations, time step, and spatial configuration with the meteorology, physics, and other transport constituents of the ARW dynamical core.
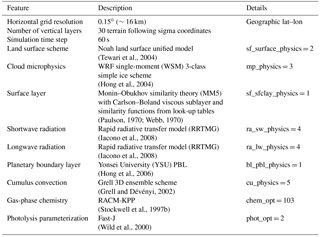
In this study, the model is configured over a single domain using the lat–lon geographical projection, with about 0.15∘ (∼16 km) horizontal grid spacing, and a domain of 165 (E–W) by 165 (N–S) grid points as shown in Fig. 6. Thirty vertical model levels were used, which correspond to a maximum height of about 20 km (∼50 hPa). Owing to its modular design, WRF-Chem provides several choices of chemical mechanisms and physics parameterizations. In this study, RACM is used for the gas-phase chemistry (Geiger et al., 2003; Stockwell et al., 1997b), and KPP is used for the integration of the species mixing ratios. The full RACM mechanism as implemented in WRF-Chem includes 75 species and 237 reactions. Table 3 summarizes the major model features and physical parameterizations as used in the simulations.
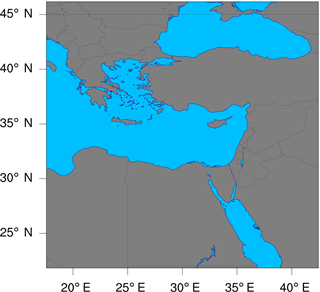
Figure 6The geographic domain utilized during the WRF-Chem simulations conducted in this study. The domain extends between 17.6 and 42.4∘ E in the longitudinal direction, and between 21.9 and 46.1∘ N in the latitudinal direction.
The meteorological fields were forced by initial and lateral boundary conditions obtained from the National Centers for the Environmental Prediction/Global Forecast System (NCEP/GFS) at a spatial resolution of 0.25∘, and updated at 3-hour intervals. MODIS-based geo-terrestrial data, including land categories, soil types, and terrain heights, were used. Our initial aim was to examine ozone mixing ratio predictions between the detailed mechanism and the skeletal mechanism using DRGEP, without the influence of any external source terms. Modelling emissions is a challenge on its own, and emissions inventories contain many uncertainties. Furthermore, these inventories always have inter-dependencies with the resolution of the mesh, the time step used, the chemical mechanism used, speciation profiling etc. This introduces uncertainties in evaluating the performance of the skeletal mechanism – including emissions would hinder the process of determining whether any errors are a result of the reduction process or a result of uncertainties in the emissions inventories. Thus, excluding emissions (at this stage) gives a clearer picture as to the effect of transport terms alone on the spatio-temporal distribution of ozone. In order to do that, anthropogenic/biogenic emissions were not utilized, and no chemical initial and boundary conditions were applied to the chemistry fields. For the latter, the model used idealized climatologically based values to initialize the chemical species instead. Further details of the initialization are given in the WRF-Chem user guide (WRF-Chem, 2017).
For the purposes of this study, two separate simulations were conducted for the period from 12 to 28 July 2017, a time of year during which ozone photochemistry is particularly active in this region. The first 5 days of the model output are considered as model spin-up time, and were excluded from our analysis. The model instantaneous, grid-cell averaged mixing ratios, were set to be written out (at the beginning of) every hour. The first simulation, used the complete (unmodified) RACM mechanism as implemented in the WRF-Chem package, while the second simulation utilized the skeletal (via DRGEP algorithm) mechanism. For a fair comparison between the two simulations, both set-ups shared the same namelist, which is included in the Supplement.
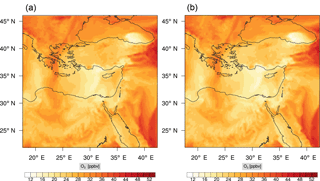
Figure 7Instantaneous comparison of the ozone spatial mixing ratio, averaged over the first nine vertical layers, using the full mechanism (a) and the skeletal mechanism (b).
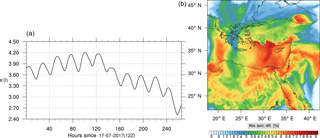
Figure 8(a) The volume-weighted average of the absolute percentage difference between the full and skeletal mechanisms, e′(t), for the ozone mixing ratio. (b) The spatial distribution of the absolute percentage difference between the reduced and full mechanisms, with respect to the full mechanism, for the ozone mixing ratio when e′(t) is maximum.
The implementation of a new chemical mechanism in WRF-Chem is a rather tedious process. This includes creating new reaction and species files, compiling KPP with the new mechanism, and writing new mechanism-specific driver and initialization routines. A work-around, is to modify the existing chemical mechanism file (in this case RACM) instead, so that it accounts for the reduced chemistry. This simple method implies that driver routines do not need to be rewritten, calls to subroutines do not need to change to account for the reduction in species, and so on. This is achieved by setting dummy reactions for all species which are removed in the skeletal mechanism. The corresponding KPP reactions in the skeletal mechanism, are included in the Supplement. From a computational perspective, the skeletal mechanism was found to be more efficient than the detailed mechanism, as expected: on 40 MPI processes, the wall-clock times using the detailed and skeletal mechanisms were 959 and 730 min, respectively. This translates to an overall gain in CPU time of 24.6 %.
This speed-up is of the same order of magnitude as in the box model runs. However due to the implementation of the skeletal mechanism in WRF-Chem (all species kept), this speed-up does not include overheads. If a new mechanism were to be written (with fewer number of species), and all relevant subroutine calls suitably modified in order to include only the species in the skeletal mechanism, an even further gain in speed-up would be expected from simulation overheads (input/output, calls to subroutines etc.).
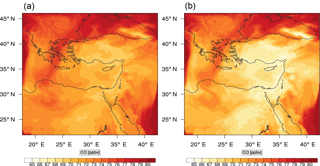
Figure 9Instantaneous comparison of the carbon monoxide spatial mixing ratio, averaged over the first nine vertical layers, using the full mechanism (a) and the skeletal mechanism (b).
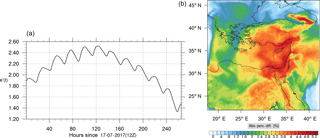
Figure 10(a) The volume-weighted average of the absolute percentage difference between the full and skeletal mechanisms, e′(t), for the carbon monoxide mixing ratio. (b) The spatial distribution of the absolute percentage difference between the reduced and the full mechanisms, with respect to the full mechanism, for the CO mixing ratio when e′(t) is maximum.
4.2 Comparison of mixing ratios
In order to warrant a more quantitative evaluation of the performance of the skeletal mechanism, we additionally calculate the volume-averaged error (based on ozone mixing ratio), in time, between the skeletal and detailed mechanisms. This is defined as
where V is the sample-space volume and Cd, Cs, are the predictions of scalar field (C) using the detailed and skeletal mechanisms, respectively. The sample volume (V) is taken to include all points in the longitudinal and latitudinal directions. In the vertical direction two different cases are considered, the lower troposphere spanning vertical levels 1–9 and the upper troposphere spanning vertical levels 10–22. The lower troposphere covers a significant section including the planetary boundary layer. The upper troposphere corresponds to altitudes from 2 to 13 km at midlatitudes. For this range, there are substantial differences in pressure, temperature, and species mixing ratios. Even though regional models are not tuned for the upper troposphere, it is still instructive to examine how the skeletal mechanism performs in this region. Mixing ratios that have zero values are not considered for the error calculation.
4.3 Lower troposphere
Figure 7 shows a direct comparison between the ozone mixing ratios as predicted using the full mechanism (left) and the skeletal mechanism (right). The instance depicted, corresponds to the case of maximum error (e′(t)). From visual inspection alone, it is clear that there is very good agreement for the spatial ozone concentration prediction using the skeletal mechanism.

Figure 11Instantaneous comparison of the formaldehyde spatial mixing ratio, averaged over the first nine vertical layers, using the full mechanism (a) and the skeletal mechanism (b).
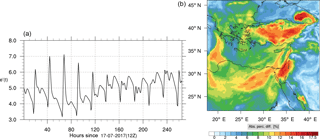
Figure 12(a) The volume-weighted average of the absolute percentage difference between the full and skeletal mechanisms, e′(t), for the formaldehyde mixing ratio. (b) The spatial distribution of the absolute percentage difference between the reduced and the full mechanisms, with respect to the full mechanism, for the formaldehyde mixing ratio when e′(t) is maximum.
The corresponding error for the ozone mixing ratio field is depicted in Fig. 8a. Over the 265 time steps (hours) included in the analysis, it is found that e′ varies between 2.52 % and 4.21 %. These small errors confirm the good agreement observed for the instantaneous ozone predictions shown in Fig. 7. Figure 8b shows the distribution of error, averaged in the vertical layers only, for the time instance of maximum, e′, i.e., at 100 h. This helps to elucidate the actual spatial distribution of the error in terms of latitude and longitude. The error distribution is also within reasonable bounds at this instance, not exceeding 10 %. Note, that this distribution applies at the instance of maximum volume-averaged error as calculated using Eq. (10). This error is actually transported during the simulation, i.e., is not specific to a particular region.
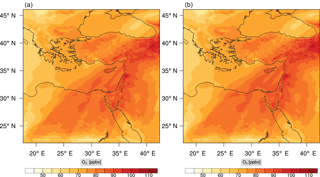
Figure 13Instantaneous comparison of the ozone spatial mixing ratio, averaged over the vertical layers 10–22, using the full mechanism (a) and the skeletal mechanism (b).
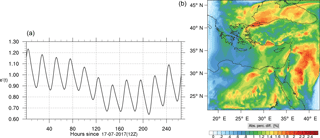
Figure 14(a) The volume-weighted average of the absolute percentage difference between the full and skeletal mechanisms, e′(t), for the ozone mixing ratio. (b) The spatial distribution of the absolute percentage difference between the reduced and the full mechanisms, with respect to the full mechanism, for the ozone mixing ratio when e′(t) is maximum.
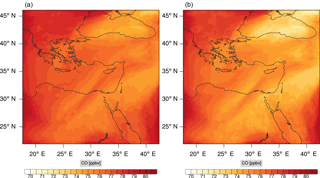
Figure 15Instantaneous comparison of the carbon monoxide spatial mixing ratio, averaged over the vertical layers 10–22, using the full mechanism (a) and skeletal mechanism (b).
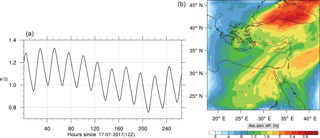
Figure 16(a) The volume-weighted average of the absolute percentage difference between the full and skeletal mechanisms, e′(t), for the carbon monoxide mixing ratio. (b) The spatial distribution of the absolute percentage difference between the reduced and the full mechanisms, with respect to the full mechanism, for the CO mixing ratio when e′(t) is maximum.
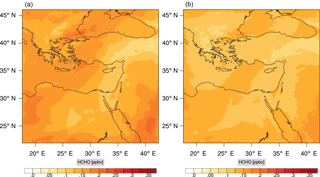
Figure 17Instantaneous comparison of the formaldehyde spatial mixing ratio, averaged over the vertical layers 10–22, using the full mechanism (a) and skeletal mechanism (b).
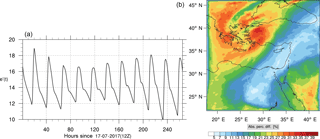
Figure 18(a) The volume-weighted average of the absolute percentage difference between the full and skeletal mechanisms, e′(t), for the formaldehyde mixing ratio. (b) The spatial distribution of the absolute percentage difference between the reduced and the full mechanisms, with respect to the full mechanism, for the formaldehyde mixing ratio when e′(t) is maximum.
Figures 9, 10 and 11, 12 show the corresponding results for carbon monoxide which is a slow reacting species, and formaldehyde which is a relatively faster reacting species. Both of these species were not included as targets during the reduction; therefore, it is instructive to examine how their mixing ratio predictions compare to ozone which was the target species. Figures 9 and 10 show that the CO predictions are also in good agreement with relatively small percentage errors. The maximum volume-weighted error (e′) for carbon monoxide during the simulation does not exceed 2.6 %. The instantaneous error averaged in the vertical layers only at the time of maximum e′ also remains low as one may observed from Fig. 10b. The errors for formaldehyde in comparison are relatively large as one may observe from the results in Figs. 11 and 12. The maximum volume-weighted error is about 7 %, while the instantaneous error for the time of maximum e′ is in the region of 20 % (Fig. 12b). Formaldehyde, which is an important intermediate species (Lelieveld et al., 2016), is involved in many oxidation reactions including a number of VOCs which explains the relatively larger errors. The same applies for the hydroxyl radical HO, which also displayed relatively large errors. In particular, for the subset mechanism including 54 species, higher alkanes such as HC3 and TOL (toluene) were identified as redundant species from the DRGEP. These species constitute an important HO consumption pathway, and excluding them leads to an overestimation of the HO mixing ratio. Much better results may be obtained by either reducing the OIC threshold (and including more species) or by including more targets during the reduction. However, both of these approaches lead to larger skeletal mechanisms and a reduction in speed-up; in other words, careful selection of the targets is required to obtain both an accurate and computationally fast mechanism.
4.4 Upper troposphere
Percentage errors, as defined above, are calculated for O3, CO, and HCHO for levels 10–22. The results are shown in Figs. 13–18, respectively. Ozone concentration predictions using the skeletal mechanism are particularly good. The maximum instantaneous error is about 1.22 %, which is lower than the corresponding error observed for the lower troposphere in Fig. 8. The error is also found to be lower for CO. The error for formaldehyde, which is a relatively faster species, is larger in comparison. Furthermore, this error is also larger than the corresponding error observed in the lower troposphere. However, ozone, which was the target species, is accurately predicted overall despite the different thermochemical conditions found at larger altitudes.
It is also important to note at this point that care should be taken when using skeletal mechanisms in regional/climate simulations. Mechanisms such as RACM have traditionally been developed with a particular application area in mind, and are usually validated against smog-chamber data over a limited set of conditions. Starting from a detailed chemical mechanism, several subset skeletal mechanisms can, in principle, be derived for particular applications of interest. Thus far, this process has not really been undertaken in a formal fashion – developers added, subtracted, or lumped species based mostly on experience, so as to match simulation results against experimental results. As indicated by Kaduwela et al. (2015), the development of atmospheric chemical mechanisms should follow a more formal process, by assimilating information on chemical kinetics, compiling detailed mechanisms, evaluating their performance, and finally reducing them for applications of interest through a formal procedure. DRGEP is one such formal reduction process which can be employed for developing skeletal mechanisms from explicit detailed mechanisms for target species/conditions of interest, other than those already considered in this study.
A direct relation graph approach for generating skeletal chemical mechanisms from more detailed mechanisms was employed, in order to produce a more computationally efficient mechanism for accelerated atmospheric chemistry simulations. A code was developed for the task, and the method was applied to a commonly used mechanism, namely RACM, with the target species being ozone, which is a major pollutant.
The skeletal mechanism was developed using input from a 0-D initial-value problem, and was validated both a priori against the 0-D problem results and a posteriori. The a posteriori validation involved implementing both the detailed and the skeletal mechanisms in an actual air-quality forecasting code, namely WRF-Chem, and running simulations to compare the spatio-temporal ozone mixing ratio profiles. The skeletal mechanism was found to perform well, with relatively low percentage errors. A speed-up of 24.6 % was achieved for the total simulation time, which does not yet include any speed-up due to overheads such as input/output computations.
The method is general, and can be applied to any chemical mechanism in the WRF-Chem package or other chemistry–transport codes, for producing computationally more efficient air quality and climate simulations. Since a significant speed-up has been achieved with the already optimized chemical mechanism used in this study, it is expected that future application to more comprehensive chemistry mechanisms may lead to significant gains in computational efficiency.
The WRF-Chem package used for the numerical simulations is available from the National Center for Atmospheric Research (NCAR): https://www2.acom.ucar.edu/wrf-chem. The WRF-Chem namelist file, and the skeletal RACM mechanism are given as supplements. The code used for the DRGEP is attached as a Supplement and can also be obtained from the authors upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-11-3391-2018-supplement.
ZN developed the DRGEP code, conducted the model-scenario (box model) simulations and developed the sub-set skeletal RACM. J-YC provided useful insight and guidance on the reduction process and code development. YP conducted the WRF-Chem simulations. JL and RS provided useful insight and comments. All authors co-wrote the manuscript.
The authors declare that they have no conflict of interest.
Zacharias Marinou Nikolaou acknowledges funding through the VI-SEEM project,
which receives funding from the European Union's H2020 research and
innovation program under grant agreement no. 675121.
Edited by: David Topping
Reviewed by: Maarten
Krol and William Stockwell
Carter, W.: Development and evaluation of the saprc-99 chemical mechanism, Air Pollution Research Center and College of Engineering Center for Environmental Research and Technology, University of California, Riverside, CA, USA, available at: http://www.cert.ucr.edu/~carter/SAPRC/ (last access: 5 March 2018), 2000. a
Chen, Y. and Chen, J.: Application of Jacobian defined direct interaction coefficient in DRGEP-based chemical mechanism reduction methods using different graph search algorithms, Combust. Flame, 174, 77–84, 2016. a
Christou, M., Christoudias, T., Morillo, J., Alvarez, D., and Merx, H.: Earth system modelling on system-level heterogeneous architectures: EMAC (version 2.42) on the Dynamical Exascale Entry Platform (DEEP), Geosci. Model Dev., 9, 3483–3491, https://doi.org/10.5194/gmd-9-3483-2016, 2016. a
Daescu, D., Sandu, A., and Carmichael, G.: Direct and Adjoint Sensitivity Analysis of Chemical Kinetic Systems with KPP: II – Validation and Numerical Experiments, Atmos. Environ., 37, 5097–5114, 2003. a
Damian, V., Sandu, A., Damian, M., Potra, F., and Carmichael, G.: The Kinetic PreProcessor KPP–A Software Environment for Solving Chemical Kinetics, Comput. Chem. Eng., 26, 1567–1579, 2002. a
Derwent, R., Jenkin, M., Saunders, S., and Pilling, M.: Photochemical ozone creation potentials for organic compounds in northwest Europe calculated with a master chemical mechanism, Atmos. Environ., 32, 2429–2441, 1998. a, b
Dijkstra, E.: A note on two problems in connexion with graphs, Numer. Math., 1, 261–271, 1959. a
Dunker, A.: The reduction and parameterisation of chemical mechanisms for inclusion in atmospheric reaction-transport models, Atmos. Environ., 20, 479–486, 1986. a, b, c
Geiger, H., Barnes, I., Bejan, I., Benter, T., and Spittler, M.: The tropospheric degradation of isoprene: an updated module for the regional atmospheric chemistry mechanism, Atmos. Environ., 37, 1503–1519, 2003. a
Gerry, M., Whitten, G., Killus, J., and Dodge, M.: A photochemical kinetics mechanism for urban and regional scale computer modelling, J. Geophys. Res., 94, 12925–12956, 1989. a
Grell, G. A. and Dévényi, D.: A generalized approach to parameterizing convection combining ensemble and data assimilation techniques, Geophys. Res. Lett., 29, 1693, https://doi.org/10.1029/2002GL015311, 2002. a
Grell, G. A., Peckham, S. E., Schmitz, R., McKeen, S. A., Frost, G., Skamarock, W. C., and Eder, B.: Fully coupled “online” chemistry within the WRF model, Atmos. Environ., 39, 6957–6975, 2005. a
Hairer, E. and Wanner, G.: Solving Ordinary Differential Equations – II. Stiff and Differential-Algebraic Problems, Springer-Verlag, Berlin, 1993. a
Hairer, E., Norsett, S., and Wanner, G.: Solving Ordinary Differential Equations – I. Nonstiff Problems, Springer-Verlag, Berlin, 1993. a
Heard, A., Pilling, M., and Tomlin, A.: Mechanism reduction techniques applied to tropospheric chemistry, Atmos. Environ., 32, 1059–1073, 1998. a, b, c, d, e, f
Hong, S.-Y., Dudhia, J., and Chen, S.-H.: A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation, Mon. Weather Rev., 132, 103–120, 2004. a
Hong, S.-Y., Noh, Y., and Dudhia, J.: A new vertical diffusion package with an explicit treatment of entrainment processes, Mon. Weather Rev., 134, 2318–2341, 2006. a
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res.-Atmos., 113, D13103, https://doi.org/10.1029/2008JD009944, 2008. a, b
Jenkin, M., Watson, L., Utembe, S., and Shallcross, D.: A Common Representative Intermediates (CRI) mechanism for VOC degradation – Part 1: Gas phase mechanism development, Atmos. Environ., 42, 7185–7195, 2008. a
Kaduwela, A., Luecken, D., Carter, W., and Derwent, R.: New directions: Atmospheric chemical mechanisms for the future, Atmos. Environ., 122, 609–610, 2015. a
Lam, S. and Goussis, D.: Understanding Complex Chemical Kinetics with Computational Singular Perturbation, 22nd Sympt. Int. Combust., 22, 931–941, 1988. a, b
Lelieveld, J., Gromov, S., Pozzer, A., and Taraborrelli, D.: Global tropospheric hydroxyl distribution, budget and reactivity, Atmos. Chem. Phys., 16, 12477–12493, https://doi.org/10.5194/acp-16-12477-2016, 2016. a
Lu, T. and Law, C.: A directed relation graph method for mechanism reduction, Proc. Combust. Inst., 30, 1333–1341, 2005. a, b, c
Mass, U. and Pope, S.: Simplifying Chemical Kinetics: Intrinsic Low-Dimensional Manifolds in Composition Space, Combust. Flame, 88, 239–264, 1992. a, b
Neophytou, M., Goussis, D., van Loon, M., and Mastorakos, E.: Reduced chemical mechanisms for atmospheric pollution using Computational Singular Perturbation analysis, Atmos. Environ., 38, 3661–3673, 2004. a, b
Niemeyer, K. and Sung, C.: On the importance of graph search algorithms for DRGEP-based mechanism reduction methods, Combust. Flame, 158, 1439–1443, 2011. a, b, c
Niemeyer, K., Sung, C., and Raju, M.: Skeletal mechanism generation for surrogate fuels using direct relation graph with error propagation and sensitivity analysis, Combust. Flame, 157, 1760–1770, 2010. a
Nikolaou, Z., Chen, J., and Swaminathan, N.: A 5-step reduced mechanism for combustion of CO/H2/H2O/CH4/CO2 mixtures with low hydrogen/methane and high H2O content, Combust. Flame, 160, 56–75, 2013. a
Nikolaou, Z., Swaminathan, N., and Chen, J.: Evaluation of a reduced mechanism for turbulent premixed combustion, Combust. Flame, 161, 3085–3099, 2014. a
Paulson, C. A.: The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer, J. Appl. Meteorol., 9, 857–861, 1970. a
Pepiot-Desjardins, P. and Pitsch, H.: An efficient error-propagation-based reduction method for large chemical kinetic mechanisms, Combust. Flame, 154, 67–81, 2008. a, b, c
Peters, N. and Rogg, B.: Reduced Reaction Mechanisms for Applications in Combustion Systems, Notes in Physics, Springer-Verlag, 15 pp., 1993. a
Pope, S.: Computationally efficient implementation of combustion chemistry using in situ adaptive tabulation, Combust. Theory Model., 1, 41–63, 1997. a
Sandu, A., Verwer, J., Blom, J., Spee, E., Carmichael, G., and Potra, F.: Benchmarking of stiff ODE solvers for atmospheric chemistry problems – II: Rosenbrock solvers, Atmos. Environ., 31, 3459–3472, 1997a. a
Sandu, A., Verwer, J., van Loon, M., Carmichaels, G., Potra, F., Dabdub, D., and Seinfeld, J.: Benchmarking of stiff ODE solvers for atmospheric chemistry problems – I: implicit vs explicit, Atmos. Environ., 31, 479–486, 1997b. a
Sandu, A., Daescu, D., and Carmichael, G.: Direct and Adjoint Sensitivity Analysis of Chemical Kinetic Systems with KPP: I – Theory and Software Tools, Atmos. Environ., 37, 5083–5096, 2003. a
Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D. M., Wang, W., and Powers, J. G.: A description of the advanced research WRF version 2, Tech. rep., National Center For Atmospheric Research Boulder Co Mesoscale and Microscale Meteorology Div., 2005. a
Stagni, A., Frassoltadi, A., Cuoci, A., Faravelli, T., and Ranzi, E.: Skeletal mechanism reduction through species-targeted sensitivity analysis, Combust. Flame, 163, 382–393, 2016. a
Stockwell, W. R., Middleton, P., Chang, J., and Tang, X.: The second generation regional acid deposition model chemical mechanism for regional air quality modeling, J. Geoph. Res., 95, 16343–16367, 1990. a
Stockwell, W. R., Kirchner, F., and Kuhn, M.: A new mechanism for regional atmospheric chemistry modeling, J. Geophys. Res., 102, 25847–25879, 1997a. a
Stockwell, W. R., Kirchner, F., Kuhn, M., and Seefeld, S.: A new mechanism for regional atmospheric chemistry modeling, J. Geophys. Res.-Atmos., 102, 25847–25879, 1997b. a, b
Tewari, M., Chen, F., Wang, W., Dudhia, J., LeMone, M., Mitchell, K., Ek, M., Gayno, G., Wegiel, J., and Cuenca, R.: Implementation and verification of the unified NOAH land surface model in the WRF model, in: 20th conference on weather analysis and forecasting/16th conference on numerical weather prediction, vol. 1115, 2004. a
Tomlin, A., Turanyi, T., and Pilling, M.: Mathematical tools for the construction, investigation and reduction of combustion mechanisms, chap. 4, Compr. Chem. Kinetics, 35, 293–247, 1997. a
Turanyi, T., Berces, T., and Vajda, S.: Reaction rate analysis of complex kinetic systems, Int. J. Chem. Kinetics, 21, 83–99, 1989. a, b, c
Webb, E. K.: Profile relationships: The log-linear range, and extension to strong stability, Q. J. Roy. Meteorol. Soc., 96, 67–90, 1970. a
Whitehouse, L. E., Tomlin, A. S., and Pilling, M. J.: Systematic reduction of complex tropospheric chemical mechanisms, Part II: Lumping using a time-scale based approach, Atmos. Chem. Phys., 4, 2057–2081, https://doi.org/10.5194/acp-4-2057-2004, 2004. a, b, c
Wild, O., Zhu, X., and Prather, M. J.: Fast-J: Accurate simulation of in-and below-cloud photolysis in tropospheric chemical models, J. Atmos. Chem., 37, 245–282, 2000. a
WRF-Chem: WRF-Chem user manual for version 3.9.1.1, available at: https://ruc.noaa.gov/wrf/wrf-chem/Users_guide.pdf (last access: 5 March 2018), 2017. a
Xia, A. G., Michelangeli, D. V., and Makar, P. A.: Mechanism reduction for the formation of secondary organic aerosol for integration into a 3-dimensional regional air quality model: a-pinene oxidation system, Atmos. Chem. Phys., 9, 4341–4362, https://doi.org/10.5194/acp-9-4341-2009, 2009. a