2.1 EMAC model

The EMAC model is a numerical chemistry-climate model which describes tropospheric and middle-atmosphere processes and their interactions with ocean, land, and human influences. Such interactions are simulated via dedicated submodels in the MESSy framework (Modular Earth Submodel System; Jöckel et al., 2010), while the 5th generation European Centre Hamburg GCM (ECHAM5; Roeckner et al., 2006) is used as core of the atmospheric dynamics. For the present study we have used ECHAM5 version 5.3.02 and MESSy version 2.53.

The EMAC model has been extensively described and evaluated against in situ observations and satellite data, e.g. aerosol optical depth, acid deposition, and meteorological parameters (e.g. Pozzer et al., 2012, 2015; Karydis et al., 2016; Tsimpidi et al., 2016; Klingmüller et al., 2018). It computes gas-phase species on-line through the MECCA (Module Efficiently Calculating the Chemistry of the Atmosphere) submodel (Sander et al., 2011) and provides a comprehensive treatment of chemical processes and dynamical feedbacks through radiation (Dietmüller et al., 2016). Aerosol microphysics and gas/aerosol partitioning are calculated by the GMXe (Global Modal-aerosol eXtension) submodel (Pringle et al., 2010), a two-moment aerosol module which predicts the number concentration and the mass mixing ratio of the aerosol modes, along with the mixing state. The aerosol size distribution is described by seven lognormal modes (defined by total number concentration, number mean radius, and geometric standard deviation): four hydrophilic modes, which cover the aerosol size spectrum of nucleation, Aitken, accumulation, and coarse modes; and three hydrophobic modes, which have the same size range except for the nucleation mode which is not required. The aerosol composition within each mode is uniform in size (internally mixed) but it varies among modes (externally mixed). The aging of aerosols, through coagulation or condensation of water vapour and sulfuric acid, is described by GMXe by transferring aerosols from the externally mixed to the internally mixed modes. Convective and large-scale clouds are separately treated and individually calculated by the submodels CONVECT and CLOUD, respectively. The CONVECT submodel contains multiple convection parameterizations (Tost et al., 2006b). In this work the scheme of Tiedtke (1989) with modifications by Nordeng (1994) has been used. Convective cloud microphysics is highly simplified and neither explicit aerosol activation into liquid droplets nor aerosol effects in the ice formation processes are taken into account, i.e. convective microphysics is solely based on temperature and updraught strength. Detrainment from convection is treated by taking updraught (and downdraught) concentrations of water vapour and cloud condensate and the corresponding mass flux detrainment rates into account. These are merged including turbulent detrainment (i.e. exchange of mass through the cloud edges) and organized detrainment (i.e. organized outflow at cloud top). The detrained water vapour is added to the large-scale water vapour field, while the detrained cloud condensate is directly used as a source term for cloud condensate by the large-scale cloud scheme (i.e. the CLOUD submodel), which considers the detrained condensate as either liquid or ice depending on the temperature (if T<238 K the phase is ice) and the updraught velocity. The number of detrained ice crystals is estimated from the ice condensate detrained from convection by assuming an only temperature dependent radius. The CLOUD submodel uses a double-moment stratiform cloud microphysics scheme for cloud droplets and ice crystals (Lohmann et al., 1999, 2007; Lohmann and Kärcher, 2002), which defines prognostic equations for specific humidity, liquid cloud mixing ratio, ice cloud mixing ratio, cloud droplet number concentration (CDNC), and ICNC. The advantage of using a two-moment scheme is that it allows aerosol–cloud interactions, improving calculations of cloud microphysical processes and radiative transfer. In the CLOUD submodel, ice crystals form via homogeneous nucleation in the cirrus regime, and via immersion and contact freezing in the mixed-phase regime (more details about ice nucleation are given in the next subsection). Cloud droplet formation is parameterized by the “unified activation framework” (UAF; Kumar et al., 2011; Karydis et al., 2011). It is an advanced physically based parameterization which merges two theories: κ-Köhler theory (KT; Petters and Kreidenweis, 2007), which governs the activation of soluble aerosols, and the Frenkel–Halsey–Hill adsorption activation theory (FHH-AT; Kumar et al., 2009), which describes the droplet activation due to water adsorption onto insoluble aerosols (e.g. mineral dust). Aerosol modes that consist of only soluble material follow the KT, and the required effective hygroscopicity (κ) is calculated based on the chemical composition of the mode as described by the ISORROPIA thermodynamic equilibrium model (Fountoukis and Nenes, 2007). Aerosol modes that consist of an insoluble core with soluble coating follow the UAF scheme, which takes into account the effects of adsorption and absorption on the cloud condensation nuclei (CCN) activity of the mixed aerosol. More details about the UAF scheme and its implementation in the EMAC model can be found in Karydis et al. (2017). The diagnostic cloud cover scheme of Sundqvist et al. (1989) based on the grid mean relative humidity is used; it assumes that a grid box is partly covered by clouds when the relative humidity exceeds a threshold and is totally covered when saturation is reached. Other microphysical processes, like phase transitions, autoconversion, aggregation, accretion, evaporation of rain, melting of snow, and sedimentation of cloud ice, are also taken into account by the CLOUD submodel. An evaluation of the double-moment cloud microphysics scheme used by ECHAM5 was presented in Lohmann et al. (2007, 2008) and Lohmann and Hoose (2009), applying the two-moment aerosol microphysics scheme HAM (Stier et al., 2005). Lauer et al. (2007) and Righi et al. (2013, 2015, 2016) showed an evaluation of the CLOUD submodel in conjunction with the aerosol microphysics submodel MADE (Ackermann et al., 1998), while Tost (2017) evaluated the CLOUD submodel in combination with the GMXe submodel. In Sect. 4 we will extend the comparison with various observations. Finally, physical loss processes, like dry deposition, wet deposition, and sedimentation of aerosol, are explicitly considered by the submodels DRYDEP, SEDI, and SCAV (Kerkweg et al., 2006; Tost et al., 2006a).

2.2 Default ice nucleation in EMAC

The CLOUD submodel describes the evolution of the prognostic variables which undergo all cloud microphysical processes (e.g. precipitation, deposition, and evaporation/sublimation). As far as the formation of new ice crystals is concerned, they are computed via two independent parameterizations, as shown in black in Fig. 1.

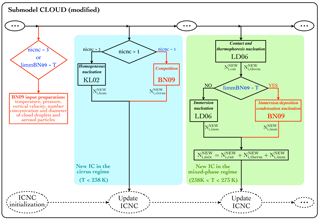
Figure 1Scheme of the new ice crystal formation in the CLOUD submodel: different ice nucleation schemes can be used in the cirrus and in the mixed-phase regimes. nicnc and limm_BN09 are variables defined in the namelist file “cloud.nml”; red parts are new; three dots indicate other processes coded in the CLOUD submodel.

Download

In the cirrus regime (T≤238.15 K) it is assumed that cirrus clouds exclusively form homogeneously using the parameterization of Kärcher and Lohmann (2002, hereafter referred to as KL02). Such parameterization computes the newly formed ice crystals via homogeneous nucleation ($N_{\mathrm{i},\mathrm{hom}}^{\mathrm{NEW}}$) of supercooled solution droplets and allows supersaturation with respect to ice. Alternatively, it is possible to use the parameterization of Kärcher and Lohmann (2003) to simulate cirrus formation via pure heterogeneous freezing; however, by default the model operates with KL02, under the assumption that the dominant freezing mechanism for cirrus clouds is homogeneous nucleation.

In the mixed-phase regime (238.15 K $<T\le \mathrm{273.15}$ K) heterogeneous nucleation occurs via immersion ($N_{\mathrm{i},\mathrm{imm}}^{\mathrm{NEW}}$) and contact ($N_{\mathrm{i},\mathrm{cnt}}^{\mathrm{NEW}}$) freezing as described in Lohmann and Diehl (2006, hereafter referred to as LD06). Insoluble dust can initiate contact nucleation in the presence of supercooled water droplets following the parameterization of Levkov et al. (1992). Soluble dust and black carbon can act as immersion nuclei, according to the stochastic freezing hypothesis described in Diehl and Wurzler (2004). Possibly, contact freezing via thermophoresis can be included ($N_{\mathrm{i},\mathrm{therm}}^{\mathrm{NEW}}$), but it is usually not considered (i.e. $N_{\mathrm{i},\mathrm{therm}}^{\mathrm{NEW}}=\mathrm{0}$) since its contribution is negligible (Lohmann and Hoose, 2009). The Wegener–Bergeron–Findeisen (WBF) process at subfreezing temperatures is parameterized, so liquid water is forced to evaporate from cloud droplets and deposit onto existing ice crystals.

In the CLOUD submodel, a single updraught velocity (w) is used for the whole grid cell, although w can vary strongly in reality within the cell horizontal dimension (e.g. Guo et al., 2008). This is a simplification which is commonly used by GCMs; nevertheless, important progress has been recently achieved on this front to describe the subgrid-scale variability in updraught velocity using high-resolution simulations (Barahona et al., 2017). In EMAC, the subgrid-scale variability in vertical velocity is introduced by a turbulent component (w_sub), which depends on the subgrid-scale turbulent kinetic energy (TKE) described by Brinkop and Roeckner (1995), such that $w_{\mathrm{sub}}=\mathrm{0.7}\sqrt{\mathrm{TKE}}$. The vertical velocity is given by the sum of the grid mean vertical velocity ($\stackrel{\mathrm{‾}}{w}$) and the turbulent contribution: $w=\stackrel{\mathrm{‾}}{w}+\mathrm{0.7}\sqrt{\mathrm{TKE}}$ (Kärcher and Lohmann, 2002). Zhou et al. (2016) analysed the effect of different updraught velocity representations on ice number concentrations and showed that using w_sub overestimates the ICNCs at temperatures below 205 K, but agrees better with the observations at higher temperatures. Other studies, e.g. Kärcher and Ström (2003) and Joos et al. (2008), showed that w is in good agreement with vertical velocity observations. Given the importance of updraught velocities for ice formation (Donner et al., 2016; Sullivan et al., 2016), future studies could implement a complete probability distribution of updraughts. Finally, the influence of the pre-existing ice particles is not taken into account. The CLOUD submodel simply reduces the number of aerosol particles available for ice nucleation by the existing ice particle number in the cirrus regime.

2.3 Ice nucleation parameterization BN09

2.4 Set-up of simulations

In this study EMAC simulations have been carried out with the T42L31ECMWF resolution, which corresponds to a spherical truncation of T42 (i.e. quadratic Gaussian grid of approx. $\mathrm{2.8}{}^{\circ }\times \mathrm{2.8}{}^{\circ }$ in latitude and longitude) and 31 vertical hybrid pressure levels up to 10 hPa (approx. 25 km) at the lower stratosphere. All simulations have been run for 6 years (1 year as spin-up time plus 5 years for the analysis) using emissions starting from the year 2000 (GFEDv3.1 from van der Werf et al., 2010, for biomass burning and CMIP5-RCP4.5 from Clarke et al., 2007, for anthropogenic emissions). As in Pozzer et al. (2012), dust is off-line prescribed using monthly emission files based on the AEROCOM dataset (Dentener et al., 2006). Also, volcanic and secondary organic aerosol emissions are based on AEROCOM, while GFEDv3.1 and CMIP5-RCP4.5 have been used to simulate emissions of black carbon and organic aerosols, respectively. Finally, aerosol climatologies have been used for the interactions with radiation (Tanre et al., 1984) and heterogeneous chemistry (Aquila et al., 2011). Prescribed climatologies of sea surface temperatures (SST) and sea-ice concentrations (SIC) from AMIP (30 years: 1980–2009) have been used as boundary conditions. Daily means have been saved as output, and monthly means have been used for the analysis in Sects. 3 and 4.1. Table 1 lists all simulations of this study and summarizes their main characteristics. The default experiment (DEF or KL+LD) is performed with the standard configuration of the EMAC model, i.e. using the parameterization of Kärcher and Lohmann (2002) for cirrus clouds and the parameterization of Lohmann and Diehl (2006) for immersion nucleation in the mixed-phase regime. The UAF scheme is used as cloud droplet formation parameterization, like in Karydis et al. (2017). In order to investigate the model performace using the BN09 scheme, we carried out three other experiments where BN09 operates in the two cloud regimes in different combinations: BN09 computing the new ice crystals in the cirrus regime (BN+LD), in the mixed-phase regime (KL+BN), and in both regimes (BN+BN).

In all experiments, contact nucleation is computed according to LD06, while thermophoresis contact nucleation is not considered since its contribution is negligible (as remarked in Sect. 2.2). The P13 parameterization is used to simulate deposition and immersion/condensation nucleation whenever BN09 is called (for the reasons explained in Sect. 2.3). Since LD06 takes into account only dust and soot for immersion nucleation, we set the same aerosol species as contributions for P13 and turned off the biological and organic contributions.

Table 1All experiments carried out in this study.

Download Print Version | Download XLSX

3.1 Annual zonal means

The annual zonal means of ICNC and ice water content (IWC) are shown as a function of latitude and altitude in Fig. 2, where the isolines at 273 and 238 K indicate the approximate bounds of cirrus and mixed-phase regimes. Despite the different ice nucleation parameterizations, ICNCs show similar qualitative patterns in all simulations, indicating the important role of atmospheric dynamics. Their numbers decrease towards lower altitudes (Fig. 2a) because the ice nucleation rate reduces with increasing temperature, while they are much higher over the mid-latitudes in the Northern Hemisphere (NH) because of larger INP concentrations and the influence of large mountain chains, e.g. the Rocky Mountains and the Himalayas. Looking at the relative changes, we note that ICNCs computed with BN09 in the cirrus regime are much lower than the default ICNCs in the upper troposphere and at high latitudes in the Southern Hemisphere (SH), where they are lower by up to 80 % (Fig. 2b). The absolute changes in the ICNC annual zonal means computed as a function of latitude and temperature (Fig. S1 in the Supplement) show that ICNCs in BN+KL are lower than the default case by 300 L⁻¹ at temperatures below 220 K. As ice crystals are formed almost exclusively via homogeneous nucleation here (not shown) and BNhom and KL02 produce the same order of magnitude of ICNCs (Barahona and Nenes, 2008), the negative bias is likely due to the PREICE effect predicted by BN09. Indeed, it has been demonstrated that homogeneous nucleation dominates in the upper troposphere in the tropics and in the SH (Haag et al., 2003; Liu et al., 2012; Barahona et al., 2017), while heterogeneous nucleation is important in the NH (Li et al., 2012; Kuebbeler et al., 2014; Storelvmo and Herger, 2014; Shi et al., 2015; Gasparini and Lohmann, 2016; Barahona et al., 2017) where cirrus clouds are formed from a combination of homogeneous and heterogeneous processes. Interestingly, ICNCs at lower altitudes are also influenced by the ice nucleation parameterization used in the cirrus regime. In fact, there is an increase in ICNCs in the mixed-phase regime probably due to a faster sedimentation of the larger ice crystals produced by BN09 in cirrus clouds, especially in the NH where there are larger sources of efficient ice-nucleating mineral dust. Overall, as remarked later in Sect. 4.1, the total ICNC in BN+LD globally decreases. The changes produced by applying BN09 in the mixed-phase regime (Fig. 2c) result from the different heterogeneous ice nucleation parameterizations used to simulate immersion nucleation, P13 vs. LD06. The changes are especially evident in the NH (more than 40 %), where mineral dust is more abundant than in the SH. As P13 produces fewer new ice crystals than LD06 (not shown), the positive biases in the mixed-phase regime are possibly due to influences from the cirrus regime (e.g. ice crystal sedimentation) and convective detrainment. Overall, the ICNC deviations in the mixed-phase regime obtained using the two different parameterizations are smaller (mostly within ±20 %) than in the cirrus regime. This is also evident from Fig. S1 in the Supplement (last row), where the absolute changes are, on average, between 200 and −200 L⁻¹ when BN09 is used in the cirrus regime and between 50 and −50 L⁻¹ when comparing KL+BN with KL+LD. Possibly, the rate associated with heterogeneous nucleation in the mixed-phase regime is masked by other processes, like sedimentation and aggregation, which also contribute to ICNC in this regime. Finally, the simulation using BN09 in both regimes combines the effects described so far (Fig. 2d). Since cirrus clouds do not occur throughout the whole year, we present in the Supplement (Fig. S2) the ICNC seasonal means for summer (June–July–August, JJA) and winter (December–January–February, DJF). The seasonal analysis helps to understand why there is cirrus occurrence at temperatures higher than 238 K, showing that the ICNC growth in the mixed-phase region predicted by BN+LD is actually very small, as expected given that the ice scheme used in the mixed-phase regime is the same as the default simulation.

The IWC pattern (Fig. 2e) qualitatively follows the ICNC distribution. It is quite symmetrical between the two hemispheres except at high latitudes in the NH, where IWC is slightly higher because of the higher values of ICNC. Particularly, IWC exhibits three local maxima: two over the mid-latitudes in both hemispheres and one in the tropics, associated with storm tracks and deep convections, respectively (Li et al., 2012), in agreement with satellite observations, e.g. Waliser et al. (2009), Li et al. (2012). The relative changes in Fig. 2f show a pattern very similar to Fig. 2b; therefore, IWC decreases where ICNC reduces (and vice versa) when BN09 is used in the cirrus regime. On the other hand, IWC in KL+BN slightly reduces (up to 20 %) in the mixed-phase regime in areas where ICNC increases, especially in the NH at high latitudes (Fig. 2g). This could be due to the different sizes of ice crystals; however, the areas with significance are rather small. Finally, BN+BN in Fig. 2h simulates an overall reduction of IWC except in the three areas with higher values of IWC described in Fig. 2e.

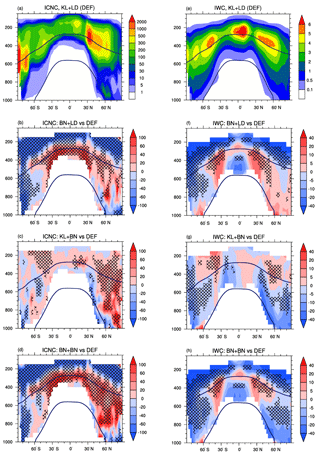
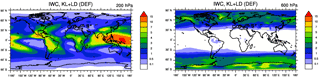
Figure 2Annual zonal means of (grid-averaged) ice crystal number concentration (ICNC, L⁻¹) and non-precipitable ice water content (IWC, mg kg⁻¹) for the default simulation KL+LD and the relative percentage changes in BN+LD, KL+BN, and BN+BN with respect to it (i.e. $\left(\text{experiment-DEF}\right)/\left|\text{DEF}\right|\cdot \mathrm{100}$), computed where ICNC^DEF≥1 L⁻¹ and IWC^DEF≥0.1 mg kg⁻¹. The isotherms at 273 and 238 K are annual means, the crossed pattern indicates areas with a significance level of 95 %.

Download

3.2 Global distributions

Figure 3 shows the global distributions of ICNC annual means at two different altitudes: 200 hPa (where temperatures vary between 200 and 220 K) to represent the cirrus regime and 600 hPa (where temperatures are approximately between 240 and 260 K) to represent the mixed-phase regime. ICNCs in the cirrus regime (Fig. 3a) show areas with high values over land and in correspondence with mountainous regions, e.g. the Rocky Mountains, Andes, and Tibetan Plateau with ICNCs >500 L⁻¹. Such a pattern is strongly related to the turbulent contribution of the vertical velocity w_sub and in agreement with Gryspeerdt et al. (2018a), who detected mostly orographic cirrus clouds in these areas. Figure 3a also shows higher ICNCs around the edge of the Antarctic ice sheet and over those regions which experience a strong convective activity, i.e. the Intertropical Convergence Zone (ITCZ) and the Tropical Warm Pool (TWP), as observed in Sourdeval et al. (2018). The annual global mean of ICNC at 200 hPa is about 200 L⁻¹ (∼390 L⁻¹ over land and ∼124 L⁻¹ over ocean). The relative changes clearly show that BN09 used in the cirrus regime (Fig. 3b, d) reduces ICNC (up to 60 %) worldwide with respect to the default experiment, and the ICNC annual global mean drops to 137 L⁻¹ (i.e. more than 30 %). As the ice crystals are mainly of homogeneous origin at this altitude, such a reduction is probably due to the PREICE effect. However, there are positive biases along the ITCZ and over the TWP area. As the concentrations of new ice crystals produced by BN09 are not particularly remarkable in these regions (not shown), convective detrainment is likely to play a role. Indeed, there is a certain response of the convective activity to the choice of the ice nucleation scheme used in the cirrus regime. On the contrary, KL+BN is characterized by a general increase in ICNC (Fig. 3c). However, most of the areas with strong positive changes (larger than 60 %) correspond to regions characterized by low ICNC (<30 L⁻¹), thus the global annual mean increases just up to 218 L⁻¹ (i.e. +9 %). At 600 hPa, ICNCs increase towards high latitudes, in particular over Greenland (up to 2000 L⁻¹) and Antarctica (mostly >2000 L⁻¹) (Fig. 3e). It must be said that, due to the very low temperatures in the latter region, even at 600 hPa the conditions are typical of the cirrus regime, and the high ICNCs can be related to the high values of both w_sub and ice supersaturation. Gryspeerdt et al. (2018a) found that cirrus clouds over Antarctica have primarily synoptic origin. However, differently from Fig. 3e, observations do not present such a high peak of ICNC over Antarctica (Gryspeerdt et al., 2018b; Sourdeval et al., 2018). The annual global mean is about 53 L⁻¹, which means about one-quarter with respect to the ICNC global mean at 200 hPa. Figure 3f confirms what was already noticed in Figure 2b, which is that the ice nucleation scheme used in the cirrus regime affects the ICNC at the mixed-phase regime altitudes predicting higher ICNCs especially in the NH. However, the largest differences occur in areas where ICNCs are very low and slightly affect the absolute ICNC values. As a result, the annual global mean actually decreases to 47 L⁻¹ because of the negative contribution in the SH. Figure 3g also shows strong positive biases, but ICNCs do not change globally (52 L⁻¹). Thus, we can reiterate that the ICNC in the mixed-phase regime is less sensitive to the ice nucleation scheme changes than the ICNC in the cirrus regime. Vertically integrated ice crystal number concentrations (ICNC_burden, Fig. S3 in the Supplement) clearly show that concentrations are higher over continents ($\sim \mathrm{48}\times {\mathrm{10}}^{\mathrm{8}}$ m⁻²), where vertical updraughts are stronger and aerosol concentrations more abundant, than over oceans ($\sim \mathrm{11}\times {\mathrm{10}}^{\mathrm{8}}$ m⁻²).

IWC at 200 and 600 hPa (Fig. 4) presents a pattern qualitatively similar to the ICNCs at the corresponding heights. Nevertheless, two interesting features appear. First, there are high IWC values (>10 mg kg⁻¹) over the TWP at 200 hPa, where ICNCs are not particularly high. This is probably caused by the larger radius of ice crystals simulated in this area. Second, IWC at 600 hPa is rather low over Antarctica (likely because of the low water vapour concentration), which is instead one of the regions with the highest ICNC. The relative changes in IWC with respect to the default simulation (Fig. S4 in the Supplement) approximately follow the changes obtained for ICNC, i.e. IWC reduces where ICNC decreases and vice versa.

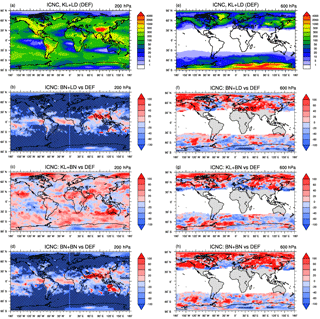
Figure 3Annual means of (grid-averaged) ice crystal number concentration (ICNC, L⁻¹) at 200 hPa (cirrus regime) and 600 hPa (mixed-phase regime) for the default simulation KL+LD and the relative percentage changes in BN+LD, KL+BN, and BN+BN with respect to it (i.e. $\left(\text{experiment-DEF}\right)/\left|\text{DEF}\right|\cdot \mathrm{100}$). The crossed pattern indicates areas with a significance level of 95 %.

Download

Figure 4Annual means of (grid-averaged) ice water content (IWC, mg kg⁻¹) at 200 hPa (cirrus regime) and 600 hPa (mixed-phase regime) for the default simulation KL+LD.

Download

4.1 Annual global means

Table 2 shows an overview of the global annual means of cloud microphysical variables and radiative fluxes computed for different observations and for all experiments, and the percentage changes with respect to the default simulation. The global vertically integrated ice crystal number concentration changes considerably depending on the ice scheme used in the cirrus regime and in the mixed-phase regime. When BN09 operates in the cirrus regime, ICNC_burden decreases by 10 % due to the competition between homogeneous and heterogeneous nucleation and the PREICE effect (a similar result has been also found by Liu et al., 2012; Kuebbeler et al., 2014; and Shi et al., 2015). On the other hand, ICNC_burden increases by almost 7 % when BN09 is used in the mixed-phase regime, i.e. when P13 simulates heterogeneous nucleation. On a large scale, these effects offset each other in BN+BN, where the global annual mean is basically unchanged with respect to the default simulation. Overall, the ICNC_burden values are very close to the global annual means found by Lohmann et al. (2008) and Kuebbeler et al. (2014), while they are 1 order of magnitude higher compared to the results of Wang and Penner (2010) and Shi et al. (2015). ICNC_burden,cirri and ICNC_burden,mixed are vertically integrated ICNCs in the cirrus regime and in the mixed-phase regime, respectively. It is interesting to quantitatively see the different contributions to the total ICNC: ICNCs_burden,cirri are about 6 times larger than the ICNCs_burden,mixed when KL02 is used and about 5 times when BN09 is applied in the cirrus regime. In general, we observe that the variability in ICNC increases when BN09 is used. Vertically integrated cloud droplet number concentration (CDNC_burden) is basically not influenced by the choice of the ice nucleation scheme. Its values are comparable with previous modelling studies (e.g. Lohmann et al., 2007; Hoose et al., 2008; Salzmann et al., 2010; Wang and Penner, 2010; Kuebbeler et al., 2014; Shi et al., 2015) and observations, although satellite observations are still affected by strong uncertainties (Bennartz and Rausch, 2017).

The ice water path (IWP) decreases by almost 7 % when BN09 is used in the cirrus regime, similarly to what has been found in Kuebbeler et al. (2014), who compared simulations assuming pure homogeneous nucleation against simulations including water vapour competition. Overall, the model underestimates the IWP, also found in other studies that applied ECHAM-HAM (e.g. Lohmann et al., 2008; Lohmann and Hoose, 2009; Kuebbeler et al., 2014; Gasparini et al., 2018); however, there are still large discrepancies among observational datasets which question the validation of the models (Duncan and Eriksson, 2018). The liquid water path (LWP) estimates derived from satellite observations vary substantially between 23 and 87 g m⁻² (Li et al., 2012; Han et al., 1994). The modelled results fall within this range and the one indicated as acceptable in Mauritsen et al. (2012), which is 50–80 g m⁻². The LWP variations among the experiments are much smaller than the IWP variations.

The absolute values of the shortwave cloud radiative effect (SCRE) and longwave cloud radiative effect (LCRE) are higher than those derived from satellite data, especially when KL02 is employed in the cirrus regime. However, when the net cloud radiative effect (NCRE) is computed, the same simulations with KL02 in the cirrus regime are closer to the observations. Looking at the absolute changes and the global distributions in the Supplement (Fig. S5) it is evident that the cloud radiative effects are sensitive to the ice nucleation scheme used for cirrus clouds. Indeed, SCRE with BN09 becomes weaker (more than 5 %) because of the less efficient scattering of shortwave radiation by fewer and larger crystals. More importantly, LCRE decreases up to 15 % in BN+LD because cirrus clouds, at the same, can trap less longwave radiation in the Earth–atmosphere system. As a result, NCRE becomes more negative, with statistical significance over some areas in the tropics and high latitudes, and the cooling effect is enhanced.

The total cloud cover (TCC) is slightly overestimated by the model (likely explaining why the cloud radiative forcing is high despite IWP being half of the observed values). However, Mauritsen et al. (2012) assert that a global model is acceptable if TCC is higher than 60 %. The changes with respect to the default simulation are very low (below 2 %), and the biggest change is in BN+LD where TCC reduces by 1.39 %, since lower ICNCs lead to higher sedimentation rates. Finally, the model tends to overestimate the total precipitation (P_tot), i.e. the sum of large scale and convective precipitations, but this has also been found with other global models (e.g. Barahona et al., 2014, with GEOS-5; Shi et al., 2015, with CAM5; and Lohmann et al., 2008, and Kuebbeler et al., 2014 with ECHAM-HAM). When BN09 is used in the cirrus regime, P_tot grows by 4 % especially because of the increase in the convective precipitation contribution, due to some feedbacks on the convective activity generated by the different ice nucleation schemes used, as mentioned in Sect. 3.2.

The annual zonal means of vertically integrated number concentration of ice crystals and cloud droplets, ice water path, liquid water path, shortwave and longwave cloud radiative effects, and total cloud cover are shown in Fig. S6 (in the Supplement) and are comparable with the literature cited before. The annual zonal mean profiles clearly show that the simulations using the same ice nucleation scheme in the cirrus regime are very close to each other, i.e. KL+LD and KL+BN, and BN+LD and BN+BN (as already visible in Table 2).

Overall, the model performs well with respect to observations and the literature. Mostly, the experiments do not yield evident differences among each other at the global scale, as regional variations may cancel out; however, there are clear effects on SCRE and LCRE from changing the cirrus ice nucleation scheme. As there is not a clear indication which simulation performs better, in the next subsection we extend our analysis including a statistical comparison with aircraft measurements.

Table 2Global annual means for simulations and observations. Shown are grid-averaged vertically integrated cloud droplet number concentration (CDNC_burden, 10¹⁰ m⁻²), vertically integrated ice crystal number concentration (ICNC_burden, 10⁸ m⁻²), vertically integrated ice crystal number concentration in the cirrus regime (ICNC_burden,cirri, 10⁸ m⁻²), vertically integrated ice crystal number concentration in the mixed-phase regime (ICNC_burden,mixed, 10⁸ m⁻²), grid-averaged liquid water path (LWP, g m⁻²) and ice water path (IWP, g m⁻²), net shortwave radiative flux (SW_NET,TOA, W m⁻²), longwave radiative flux (LW_TOA, W m⁻²), and radiative imbalance (Imbalance_TOA, W m⁻²) at TOA, shortwave cloud radiative effect (SCRE, W m⁻²), longwave cloud radiative effect (LCRE, W m⁻²), net cloud radiative effect (NCRE, W m⁻²), total cloud cover (TCC, %), and total precipitation (P_tot, mm day⁻¹). The values in brackets are (temporal) standard deviations. The sixth column contains the annual global means computed using the satellite data from ERBE 1985–1990¹ and 2000–2006⁴, CERES-SYN1deg 2004–2010², CERES-EBAF 2000–2016³, MODIS-TERRA 2004–2008⁵, CMAP 1970–2016⁶, GPCP 1979–2009⁷, and global means taken from the literature: ^a is derived from AVHRR data (Gettelman et al., 2010), ^b from NOAA-9 and NOAA-10 data (Han et al., 1994), ^c from CloudSat data (Li et al., 2012), and ^d from ISCCP data (Storelvmo et al., 2008). The last three columns show the percentage changes (%) of the experiments 2, 3, and 4 with respect to the default simulation, i.e. $\left(\text{experiment-DEF}\right)/\left|\mathrm{DEF}\right|\cdot \mathrm{100}$.

Download Print Version | Download XLSX

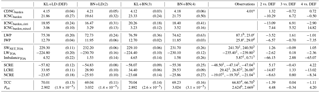
Figure 5In-cloud ice crystal number concentrations (ICNC_in−cloud, L⁻¹) versus temperature for modelled results and flight measurements. Medians are computed for modelled results (using daily means between 25^∘ S and 75^∘ N, masking ICNC_in-cloud<0.1 L⁻¹, i.e. the minimum observed value) and observations, for each 1 K temperature bin. They are shown with coloured lines: KL+LD (blue), BN+LD (green), KL+BN (light blue), BN+BN (red), and observations (black). Darker gray/red colours indicate the observations/BN+BN between the 25th and 75th percentiles, while lighter gray/red colours indicate the observations/BN+BN between the 5th and 95th percentiles. (a) Cirrus regime: the modelled medians are computed approximately in the range of 4–20 km height, the observations come from Martina Krämer (personal communication, not yet published, 2017). (b) Mixed-phase regime: the modelled medians are computed approximately in the range of 0–20 km height, the observations belong to the projects WISP-94 (solid line) and ICE-L (dashed line) and concern INP concentrations.

Download

4.2 Comparison with aircraft measurements

The validation of climate models with measurements from field experiments or aircraft campaigns is always limited by the fact that the models have difficulties to capture individual meteorological events. Nevertheless, here we consider a large collection of aircraft measurements recorded over 15 years, between 1999 and 2014 (Martina Krämer, personal communication, not yet published, 2017). Eighteen field campaigns (in total, 113 flights with about 127 h in cirrus clouds) covered Europe, Australia, Africa, Seychelles, Brazil, the USA, Costa Rica, and the tropical Pacific (i.e. between 25^∘ S and 75^∘ N) in the temperature range of 185–243 K. This extensive observational dataset is compared to the modelled in-cloud ICNCs in Fig. 5a. The observed ICNC varies between 8 and 80 L⁻¹ over the entire temperature range, and the lower and upper quartiles vary between 0.6 and 300 L⁻¹. Again, the simulations can be grouped into two sets according to the ice nucleation scheme used in the cirrus regime, i.e. KL+LD/KL+BN and BN+LD/BN+BN, because of their similarities. For most of the temperature range, the simulations which use KL02 in the cirrus regime overestimate the observed ICNCs (although they mostly remain below the 75th percentile). The overestimation of ICNCs is common to other modelling studies (e.g. Wang and Penner, 2010; Liu et al., 2012; Shi et al., 2015) and especially in cold cirrus clouds (for T<205 K). On the other hand, the simulations which use BN09 in the cirrus regime are very close to the observations at temperatures below 200 K and between 220 and 230 K, while they underestimate ICNCs between 200 and 220 K. In this temperature range the simulations can exceed the observed 25th percentile (although remaining within the 5th percentile). In comparison with the other two simulations, BN+LD and BN+BN always predict lower ICNCs at temperatures below 230 K, as expected because of the competition and PREICE effects. Finally, all four simulations overestimate ICNCs by 1 order of magnitude in the temperature range 230–240 K.

Overall, the simulations BN+LD and BN+BN agree particularly well with the measurements at temperatures lower than 200 K but underestimate the ICNCs within the interval 200–220 K, due to an overestimation of the competitive nucleation and PREICE effects. Barahona et al. (2010) showed that the competitive nucleation effect is small using P13. Also, Liu et al. (2012) found that BN09 (using the parameterization of Phillips et al., 2008, for heterogeneous nucleation) and BNhom produced very similar results in the cirrus regime, suggesting that the competitive nucleation effect was small because of the low ICNCs formed heterogeneously. Thus, we can deduce that the PREICE effect is the one which is likely overestimated in our simulations. Interestingly, modelled ICNCs do not show any particular trend, as with Kuebbeler et al. (2014) who used ECHAM-HAM. Disagreeing, other studies found that ICNCs are inversely proportional with temperature, e.g. Liu et al. (2012) and Shi et al. (2015) with CAM5 (using both the ice nucleation scheme of Liu and Penner (2005) and BN09) and Barahona et al. (2010) with GEOS-5 and BN09. Such distinct behaviours are likely derived from the wide model variabilities in reproducing subgrid-scale processes, like vertical velocity, which play a role in ice nucleation. We reiterate that ICNC is highly dependent on the vertical velocity which is usually poorly represented in terms of spatial and temporal variability (Barahona et al., 2017).

For further information, in Fig. 5b we also show the modelled in-cloud ICNCs in the mixed-phase regime, considering the same latitudes as the case before (25^∘ S–75^∘ N). The simulations do not show significant differences among each other. The distinctive features are the ICNC decrease with increasing temperatures and a positive “bulge” between 265 and 270 K caused by secondary ice production (rime splintering). The modelled ICNCs are in quite good agreement with two data sets of flight measurements taken from the projects Winter Icing and Storms Project (WISP-94) and Ice in Clouds Experiment–Layer Clouds (ICE-L), which consider about 99 and 46 flight hours, respectively. It is important to stress that this comparison is less accurate than the previous one because the observations here are much more limited both in time and in space than the extensive observational data used for the cirrus regime. It should also be noted that the measurements actually concern INPs. When the INP number is not high enough to deplete the ambient supersaturation, INP concentrations and ICNCs can correspond; however, it is well known that the two concentrations show discrepancies with increasing temperature because of the secondary ice formation (Kanji et al., 2017). Finally, ICNCs in Fig. 5b are in good agreement with the results of Heymsfield et al. (2013), also based on flight campaigns. They found that ICNCs decrease as temperature increases and are within the range 5–50 L⁻¹ in the mixed-phase regime.

Besides the flight measurements, the recent ICNC estimates from lidar–radar satellite retrievals must be mentioned, e.g. Sourdeval et al. (2018) and Gryspeerdt et al. (2018b). In particular, Gryspeerdt et al. (2018b) analysed the behaviour of ICNCs within clouds as a function of temperature. Contrary to Fig. 5a, they showed that there is a weak temperature dependence of ICNC, which increases with decreasing temperature. On the other hand, similarly to Fig. 5, they found a small increase in ICNC around 265–270 K, and, interestingly, a small peak at about 233 K due to orographic and frontal regimes, which could explain our higher modelled ICNCs between 230 and 240 K.