the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Devito (v3.1.0): an embedded domain-specific language for finite differences and geophysical exploration
Mathias Louboutin
Michael Lange
Fabio Luporini
Navjot Kukreja
Philipp A. Witte
Felix J. Herrmann
Paulius Velesko
Gerard J. Gorman
We introduce Devito, a new domain-specific language for implementing high-performance finite-difference partial differential equation solvers. The motivating application is exploration seismology for which methods such as full-waveform inversion and reverse-time migration are used to invert terabytes of seismic data to create images of the Earth's subsurface. Even using modern supercomputers, it can take weeks to process a single seismic survey and create a useful subsurface image. The computational cost is dominated by the numerical solution of wave equations and their corresponding adjoints. Therefore, a great deal of effort is invested in aggressively optimizing the performance of these wave-equation propagators for different computer architectures. Additionally, the actual set of partial differential equations being solved and their numerical discretization is under constant innovation as increasingly realistic representations of the physics are developed, further ratcheting up the cost of practical solvers. By embedding a domain-specific language within Python and making heavy use of SymPy, a symbolic mathematics library, we make it possible to develop finite-difference simulators quickly using a syntax that strongly resembles the mathematics. The Devito compiler reads this code and applies a wide range of analysis to generate highly optimized and parallel code. This approach can reduce the development time of a verified and optimized solver from months to days.
Large-scale inversion problems in exploration seismology constitute some of the most computationally demanding problems in industrial and academic research. Developing computationally efficient solutions for applications such as seismic inversion requires expertise ranging from theoretical and numerical methods for optimization constrained by a partial differential equation (PDE) to the low-level performance optimization of PDE solvers. Progress in this area is often limited by the complexity and cost of developing bespoke wave propagators (and their discrete adjoints) for each new inversion algorithm or formulation of wave physics. Traditional software engineering approaches often lead developers to make critical choices regarding the numerical discretization before manual performance optimization for a specific target architecture and making it ready for production. This workflow of bringing new algorithms into production, or even to a stage that they can be evaluated on realistic datasets, can take many person months or even person years. Furthermore, it leads to mathematical software that is not easily ported, maintained, or extended. In contrast, the use of high-level abstractions and symbolic reasoning provided by domain-specific languages (DSLs) can significantly reduce the time it takes to implement and verify individual operators for use in inversion frameworks, as has already been shown for the finite-element method (Logg et al., 2012; Rathgeber et al., 2015; Farrell et al., 2013).
State-of-the-art seismic imaging is primarily based upon explicit finite-difference schemes due to their relative simplicity and ease of implementation (Virieux, 1986; Symes, 2015a; Weiss and Shragge, 2013). When considering how to design a DSL for explicit finite-difference schemes, it is useful to recognize the algorithm as being primarily a subclass of stencil algorithms or polyhedral computation (Henretty et al., 2013; Andreolli et al., 2015; Yount, 2015). However, stencil compilers lack two significant features required to develop a DSL for finite differences: symbolic computational support required to express finite-difference discretizations at a high level, enabling these expressions to be composed and manipulated algorithmically; and support for algorithms that are not stencil-like, such as source and receiver terms that are both sparse and unaligned with the finite-difference grid. Therefore, the design aims behind the Devito DSL can be summarized as
-
creating a high-level mathematical abstraction for programming finite differences to enable composability and algorithmic optimization;
-
insofar as possible using existing compiler technologies to optimize the affine loop nests of the computation, which account for most of the computational cost; and
-
developing specific extensions for other parts of the computation that are non-affine (e.g., source and receiver terms).
The first of these aims is primarily accomplished by embedding the DSL in Python and leveraging the symbolic mathematics package Sympy (Meurer et al., 2017). From this starting point, an abstract syntax tree is generated and standard compiler algorithms can be employed to either generate optimized and parallel C code or to write code for a stencil DSL – which itself will be passed to the next compiler in the chain. The fact that this can all be performed just in time (JIT) means that a combination of static and dynamic analysis can be used to generate optimized code. However, in some circumstances, one might also choose to compile offline.
The use of symbolic manipulation, code generation, and just-in-time compilation allows for the definition of individual wave propagators for inversion in only a few lines of Python code, while aspects such as varying the problem discretization become as simple as changing a single parameter in the problem specification, for example changing the order of the spatial discretization (Louboutin et al., 2017a). This article explains what can be accomplished with Devito, showing how to express real-life wave propagators as well as their integration within larger workflows typical of seismic exploration, such as the popular full-waveform inversion (FWI) and reverse-time migration (RTM) methods. The Devito compiler, and in particular how the user-provided SymPy equations are translated into high-performance C, are also briefly summarized, although for a complete description the interested reader should refer to Luporini et al. (2018).
The remainder of this paper is structured as follows: first, we provide a brief history of optimizing compilers, DSL, and existing wave-equation seismic frameworks. Next, we highlight the core features of Devito and describe the implementation of the featured wave-equation operators in Sect. 3. We outline the seismic inversion theory in Sect. 4. Code verification and analysis of accuracy in Sect. 5 are followed by a discussion of the propagator computational performance in Sect. 6. We conclude by presenting a set of realistic examples, such as seismic inversion and computational fluid dynamics, and a discussion of future work.
Improving the runtime performance of a critical piece of code on a particular computing platform is a nontrivial task that has received significant attention throughout the history of computing. The desire to automate the performance optimization process itself across a range of target architectures is not new either, although it is often met with skepticism. Even the very first compiler, A0 (Hopper, 1952), was received with resistance, as best summarized in the following quote (Jones, 1954):
Dr. Hopper believes … that the result of a compiling technique should be a routine just as efficient as a hand tailored routine. Some others do not completely agree with this. They feel the machine-made routine can approach hand tailored coding, but they believe there are “tricks of the trade” that apply to various special cases that a computer cannot be expected to utilize.
Given the challenges of porting optimized codes to a wide range of rapidly evolving computer architectures, it seems natural to again raise the layer of abstraction and use compiler techniques to replace much of the manual labor.
Community acceptance of these new “automatic coding systems” began when concerns about the performance of the generated code were addressed by the first “optimizing compiler”, Fortran, released in 1957 – which not only translated code from one language to another but also ensured that the final code performed at least as good as a handwritten low-level code (Backus, 1978). Since then, as program and hardware complexity rose, the same problem has been solved over and over again, each time by the introduction of higher levels of abstractions. The first high-level languages and compilers were targeted at solving a large variety of problems and hence were restricted in the kind of optimizations they could leverage. As these generic languages became commonplace and the need for further improvement in performance was felt, restricted languages focusing on smaller problem domains were developed that could leverage more “tricks of the trade” to optimize performance. This led to the proliferation of DSLs for broad mathematical domains or sub-domains, such as APL (Iverson, 1962), Mathematica, MATLAB®, and R.
In addition to these relatively general mathematical languages, more specialized frameworks targeting the automated solution of PDEs have long been of interest (Cárdenas and Karplus, 1970; Umetani, 1985; Cook Jr., 1988; Van Engelen et al., 1996). More recent examples not only aim to encapsulate the high-level notation of PDEs, but are often centered around a particular numerical method. Two prominent contemporary projects based on the finite-element method (FEM), FEniCS (Logg et al., 2012) and Firedrake (Rathgeber et al., 2015), both implement a common DSL, UFL (Alnæs et al., 2014), that allows for the expression of variational problems in weak form. Multiple DSLs to express stencil-like algorithms have also emerged over time (Henretty et al., 2013; Zhang and Mueller, 2012; Christen et al., 2011; Unat et al., 2011; Köster et al., 2014; Membarth et al., 2012; Osuna et al., 2014; Tang et al., 2011; Bondhugula et al., 2008; Yount, 2015). Other stencil DSLs have been developed with the objective of solving PDEs using finite differences (Hawick and Playne, 2013; Arbona et al., 2017; Jacobs et al., 2016). However, in all cases their use in seismic imaging problems (or even more broadly in science and engineering) has been limited by a number of factors other than technology inertia. Firstly, they only raise the abstraction to the level of polyhedral-like (affine) loops. As they do not generally use a symbolic mathematics engine to write the mathematical expressions at a high level, developers must still write potentially complex numerical kernels in the target low-level programming language. For complex formulations, this process can be time-consuming and error prone, as hand-tuned codes for wave propagators can reach thousands of lines of code. Secondly, most DSLs rarely offer enough flexibility for extension beyond their original scope (e.g., sparse operators for source terms and interpolation), making it difficult to work the DSL into a more complex science or engineering workflow. Finally, since finite-difference wave propagators only form part of the overarching PDE-constrained (wave-equation) optimization problem, composability with external packages, such as the SciPy optimization toolbox, is a key requirement that is often ignored by self-contained stand-alone DSLs. The use of a fully embedded Python DSL, on the other hand, allows users to leverage a variety of higher-level optimization techniques through a rich variety of software packages provided by the scientific Python ecosystem.
Moreover, several computational frameworks for seismic imaging exist, although they provide varying degrees of abstraction and are typically limited to a single representation of the wave equation. IWAVE (Symes et al., 2011; Symes, 2015a, b; Sun and Symes, 2010), although not a DSL, provides a high level of abstraction and a mathematical framework to abstract the algebra related to the wave equation and its solution. IWAVE provides a rigorous mathematical abstraction for linear operations and vector representations including Hilbert space abstraction for norms and distances. However, its C++ implementation limits the extensibility of the framework to new wave equations. Other software frameworks, such as Madagascar (Fomel et al., 2013), offer a broad range of applications. Madagascar is based on a set of subroutines for each individual problem and offers modeling and imaging operators for multiple wave equations. However, the lack of high-level abstraction restricts its flexibility and interfacing with high-level external software (i.e., Python, Java). The subroutines are also mostly written in C or Fortran and limit the architecture portability.
In general, the majority of the computational workload in wave-equation-based seismic inversion algorithms arises from computing solutions to discrete wave equations and their adjoints. There are a wide range of mathematical models used in seismic imaging that approximate the physics to varying degrees of fidelity. To improve development and innovation time, including code verification, we describe the use of the symbolic finite-difference framework Devito to create a set of explicit matrix-free operators of arbitrary spatial discretization order. These operators are derived, for example, from the acoustic wave equation
where is the squared slowness with c(x), the spatially dependent speed of sound, the symbol Δu(t,x) denotes the Laplacian of the wave field u(t,x), and q(t,x) is a source usually located at a single location xs in space (). This formulation will be used as a running example throughout the section.
3.1 Code generation – an overview
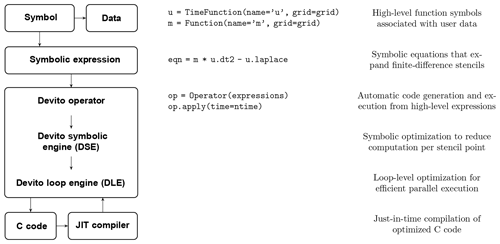
Figure 1Overview of the Devito architecture and the associated example workflow. Devito's top-level API allows users to generate symbolic stencil expressions using data-carrying function objects that can be used for symbolic expressions via SymPy. From this high-level definition, an operator then generates, compiles, and executes high-performance C code.
Devito aims to combine the performance benefits of dedicated stencil
frameworks (Bondhugula et al., 2008; Tang et al., 2011; Henretty et al., 2013; Yount, 2015) with the
expressiveness of symbolic PDE-solving DSLs (Logg et al., 2012; Rathgeber et al., 2015) through
automated code generation and optimization from high-level symbolic expressions
of the mathematics. Thus, the primary design objectives of the Devito DSL are
to allow users to define explicit finite-difference operators for
(time-dependent) PDEs in a concise symbolic manner and provide an API that is
flexible enough to fully support realistic scientific use cases. To this end,
Devito offers a set of symbolic classes that are fully compatible with the
general-purpose symbolic algebra package SymPy that enables users to derive
discretized stencil expressions in symbolic form. As we show in
Fig. 1, the primary symbols in such expressions are
associated with user data that carry domain-specific metadata information to be
used by the compiler engine (e.g., dimensions, data type, grid). The discretized
expressions form an abstract operator definition that Devito uses to generate
low-level C code (C99) and OpenMP at runtime. The encapsulating
Operator object can be used to execute the generated code from within
the Python interpreter, making Devito natively compatible with the wide range of
tools available in the scientific Python software stack. We manage memory using our
own allocators (e.g., to enforce alignment and NUMA optimizations) and therefore we also take control
over freeing memory. We wrap everything with the NumPy array API to ensure interoperability with other modules that use NumPy.
A Devito Operator takes as input a collection of symbolic expressions
and progressively lowers the symbolic representation to semantically equivalent
C code. The code generation process consists of a sequence of compiler passes
during which multiple automated performance optimization techniques are
employed. These can be broadly categorized into two classes and are performed
by distinct sub-packages.
-
Devito symbolic engine (DSE). Symbolic optimization techniques, such as common sub-expression elimination (CSE), factorization, and loop-invariant code motion, are utilized to reduce the number of floating point operations (flops) performed within the computational kernel (Luporini et al., 2015). These optimization techniques are inspired by SymPy but are custom implemented in Devito and do not rely on the SymPy implementation of CSE, for example.
-
Devito loop engine (DLE). Well-known loop optimization techniques, such as explicit vectorization, thread-level parallelization, and loop blocking with auto-tuned block sizes, are employed to increase the cache utilization and thus memory bandwidth utilization of the kernels.
A complete description of the compilation pipeline is provided in Luporini et al. (2018).

Figure 3Example code defining the two-dimensional wave equation without damping using Devito symbols and symbolic processing utilities from SymPy. Assuming , and s=Δt, the output is equivalent to Eq. (1) without the source term qs.
3.2 Discrete function symbols
The primary user-facing API of Devito allows for the definition of complex stencil operators from a concise mathematical notation. For this purpose, Devito relies strongly on SymPy (Devito 3.1.0 depends upon SymPy 1.1, and all dependency versions are specified in Devito's requirements file). Devito provides two symbolic object types that mimic SymPy symbols, enabling the construction of stencil expressions in symbolic form.
-
Function. The primary class of symbols provided by Devito behaves like
sympy.Functionobjects, allowing for symbolic differentiation via finite-difference discretization and general symbolic manipulation through SymPy utilities. Symbolic function objects encapsulate state variables (parameters and solution of the PDE) in the operator definition and associated user data (function value) with the represented symbol. The metadata, such as grid information and numerical type, which provide domain-specific information to the Devito compiler, are also carried by thesympy.Functionobject. -
Dimension. Each
sympy.Functionobject defines an iteration space for stencil operations through a set ofDimensionobjects that are used to define and generate the corresponding loop structure from the symbolic expressions.
In addition to sympy.Function and Dimension symbols, Devito
supplies the construct Grid, which encapsulates the definition of
the computational domain and defines the discrete shape (number of grid points,
grid spacing) of the function data. The number of spatial dimensions is
hereby derived from the shape of the Grid object and inherited by all
Function objects, allowing for the same symbolic operator definitions to
be used for two- and three-dimensional problem definitions. As an example, a
two-dimensional discrete representation of the square slowness of an acoustic
wave m[x,y] inside a 5 × 6 grid point domain can be created as a
symbolic function object as illustrated in Fig. 2.
It is important to note here that m[x,y] is constant in time, while
the discrete wave field is time dependent. Since time is
often used as the stepping dimension for buffered stencil operators, Devito
provides an additional function type TimeFunction, which
automatically adds a special TimeDimension object to the list of
dimensions. TimeFunction objects derive from Function with
an extra time dimension and inherit all the symbolic properties. The creation
of a TimeFunction requires the same parameters as a
Function, with an extra optional time_order property that
defines the discretization order for the time dimension and an integer
save parameter that defines the size of the time axis when the full
time history of the field is stored in memory. In the case of a buffered time
dimension save is equal to None and the size of the
buffered dimension is automatically inferred from the time_order
value. As an example, we can create an equivalent symbolic representation of
the wave field as u = TimeFunction(name='u', grid=grid), which is
denoted symbolically as u(t, x, y).
3.2.1 Spatial discretization
The symbolic nature of the function objects allows for the automatic derivation of
discretized finite-difference expressions for derivatives. Devito
Function objects provide a set of shorthand notations that allow users
to express, for example, as u.dx
and as u.dx2. Moreover, the
discrete Laplacian, defined in three dimensions as , can be expressed in shorthand simply
as u.laplace. The shorthand expression u.laplace is agnostic
to the number of spatial dimensions and may be used for two- or
three-dimensional problems.
The discretization of the spatial derivatives can be defined for any order. In the most general case, we can write the spatial discretization in the x direction of order k (and equivalently in the y and z direction) as
where hx is the discrete grid spacing for the dimension x, the constants in αj are the coefficients of the finite-difference scheme, and the spatial discretization error is of order .
3.2.2 Temporal discretization
We consider here a second-order time discretization for the acoustic wave equation, as higher-order time discretization requires us to rewrite the PDE (Seongjai Kim, 2007). The discrete second-order time derivative with this scheme can be derived from the Taylor expansion of the discrete wave field as
In this expression, Δt is the size of a discrete time step. The discretization error is O(Δt2) (second order in time) and will be verified in Sect. 5.
Following the convention used for spatial derivatives, the above expression can
be automatically generated using the shorthand expression u.dt2.
Combining the temporal and spatial derivative notations, and ignoring the
source term q, we can now define the wave propagation component of
Eq. (1) as a symbolic expression via Eq(m * u.dt2 - u.laplace, 0), where Eq is the SymPy representation of an equation.
In the resulting expression, all spatial and temporal derivatives are expanded
using the corresponding finite-difference terms. To define the propagation of
the wave in time, we can now rearrange the expression to derive a stencil
expression for the forward stencil point in time, , denoted by the shorthand expression u.forward. The forward
stencil corresponds to the explicit Euler time stepping that updates the next
time step u.forward from the two previous ones u and
u.backward (Eq. 2). We use the SymPy utility
solve to automatically derive the explicit time-stepping scheme, as
shown in Fig. 3 for the second order in space discretization.
The iteration over time to obtain the full solution is then generated by the
Devito compiler from the time dimension information. Solving the wave equation
with the above explicit Euler scheme is equivalent to a linear system
A(m)u=qs, where the vector u is the
discrete wave field solution of the discrete wave equation, qs is the
source term, and A(m) is the matrix representation of the
discrete wave equation. From Eq. (2) we can see that the matrix
A(m) is a lower triangular matrix that reflects the
time-marching structure of the stencil. Simulation of the wave field is
equivalent to a forward substitution (solve row by row from the top) on the
lower triangular matrix A(m). Since we do not consider complex
valued PDEs, the adjoint of A(m) is equivalent to its
transpose denoted as A⊤(m) and is an upper triangular
matrix. The solution v of the discrete adjoint wave equation
for an adjoint source qa
is equivalent to a backward substitution (solve from the bottom row to top row) on
the upper triangular matrix A(m)⊤ and is simulated
backward in time starting from the last time step. These matrices are never
explicitly formed, but are instead matrix-free operators with implicit
implementation of the matrix–vector product,
as a forward stencil. The stencil
for the adjoint wave equation in this self-adjoint case would simply be
obtained with solve(eqn, u.backward) and the compiler will detect the
backward-in-time update.
3.2.3 Boundary conditions
The field recorded data are measured on a wave field that propagates in an infinite domain. However, solving the wave equation in a discrete infinite domain is not feasible with finite differences. In order to mimic an infinite domain, absorbing boundary conditions (ABCs) or perfectly matched layers (PMLs) are necessary (Clayton and Engquist, 1977). These two methods allow for the approximation of the wave field as it is in an infinite medium by damping and absorbing the waves within an extra layer at the limit of the domain to avoid unnatural reflections from the edge of the discrete domain.
The least computationally expensive method is the absorbing boundary condition that adds a single damping mask in a finite layer around the physical domain. This absorbing condition can be included in the wave equation as
The parameter is equal to 0 inside the physical domain and increasing from inside to outside within the damping layer. The dampening parameter η can follow a linear or exponential curve depending on the frequency band and width of the dampening layer. For methods based on more accurate modeling, for example in simulation-based acquisition design (Liu and Fomel, 2011; Wason et al., 2017; Naghizadeh and Sacchi, 2009; Kumar et al., 2015), a full implementation of the PML will be necessary to avoid weak reflections from the domain limits.
3.2.4 Sparse point interpolation
Seismic inversion relies on data-fitting algorithms, and hence we need to support sparse operations such as source injection and wave field () measurement at arbitrary grid locations. Both operations occur at sparse domain points, which do not necessarily align with the logical Cartesian grid used to compute the discrete solution . Since such operations are not captured by the finite-difference abstractions for implementing PDEs, Devito implements a secondary high-level representation of sparse objects (Lange et al., 2017) to create a set of SymPy expressions that perform polynomial interpolation within the containing grid cell from predefined coefficient matrices.
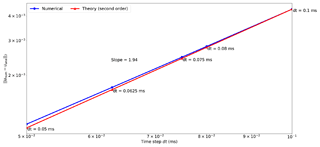
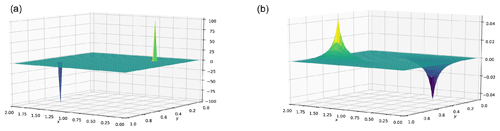
Figure 10Time discretization convergence analysis for a fixed grid, fixed propagation time (150 ms), and varying time step values. The result is plotted in a logarithmic scale and the numerical convergence rate (1.94 slope) shows that the numerical solution is accurate.
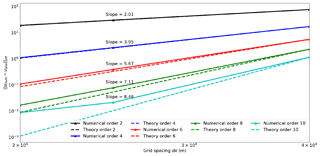
Figure 11Comparison of the numerical convergence rate of the spatial finite-difference scheme with the theoretical convergence rate from the Taylor theory. The theoretical rates are the dotted line with the corresponding colors. The result is plotted in a logarithmic scale to highlight the convergence orders as linear slopes and the numerical convergence rates show that numerical solution is accurate.
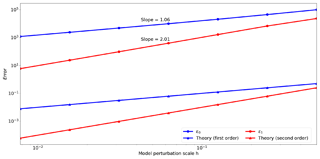
Figure 12Gradient test for the acoustic propagator. The first-order (blue) and second-order (red) errors are displayed in logarithmic scales to highlight the slopes. The numerical convergence order (1.06 and 2.01) shows that we have a correct implementation of the FWI operators.
The necessary expressions to perform interpolation and injection are
automatically generated through a dedicated symbol type,
SparseFunction, which associates a set of coordinates with the symbol
representing a set of nonaligned points. For example, the syntax
p.interpolate(expr) provided by a SparseFunction p will
generate a symbolic expression that interpolates a generic expression
expr onto the sparse point locations defined by p, while
p.inject(field, expr) will evaluate and add expr to each
enclosing point in field. The generated SymPy expressions are passed
to Devito Operator objects alongside the main stencil expression to be
incorporated into the generated C kernel code. A complete setup of the acoustic
wave equation with absorbing boundaries, injection of a source function, and
measurement of wave fields via interpolation at receiver locations can be found
in Sect. 4.2.
Seismic inversion methods aim to reconstruct physical parameters or an image of the Earth's subsurface from multi-experiment field measurements. For this purpose, a wave is generated at the ocean surface that propagates through to the subsurface and creates reflections at the discontinuities of the medium. The reflected and transmitted waves are then captured by a set of hydrophones that can be classified as either moving receivers (cables dragged behind a source vessel) or static receivers (ocean bottom nodes or cables). From the acquired data, physical properties of the subsurface such as wave speed or density can be reconstructed by minimizing the misfit between the recorded measurements and the numerically modeled seismic data.
4.1 Full-waveform inversion
Recovering the wave speed of the subsurface from surface seismic measurements is commonly cast into a nonlinear optimization problem called full-waveform inversion (FWI). The method aims at recovering an accurate model of the discrete wave velocity, c, or alternatively the square slowness of the wave, (not an overload), from a given set of measurements of the pressure wave field u. Lions (1971), Tarantola (1984), Virieux and Operto (2009), and Haber et al. (2012) show that this can be expressed as a PDE-constrained optimization problem. After elimination of the PDE constraint, the reduced objective function is defined as
where Pr is the sampling operator at the receiver locations, (T is the transpose or adjoint) is the injection operator at the source locations, A(m) is the operator representing the discretized wave-equation matrix, u is the discrete synthetic pressure wave field, qs is the corresponding pressure source, and d is the measured data. While we consider the acoustic isotropic wave equation for simplicity here, in practice, multiple implementations of the wave-equation operator A(m) are possible depending on the choice of physics. In the most advanced case, m would not only contain the square slowness but also anisotropic or orthorhombic parameters.
To solve this optimization problem with a gradient-based method, we use the adjoint-state method to evaluate the gradient (Plessix, 2006; Haber et al., 2012):
where nt is the number of computational time steps, is the data residual (difference between the measured data and the modeled data), J is the Jacobian operator, and vtt is the second-order time derivative of the adjoint wave field that solves
The discretized adjoint system in Eq. (4) represents an upper triangular matrix that is solvable by modeling wave propagation backwards in time (starting from the last time step). The adjoint-state method therefore requires a wave-equation solve for both the forward and adjoint wave fields to compute the gradient. An accurate and consistent adjoint model for the solution of the optimization problem is therefore of fundamental importance.
4.2 Acoustic forward modeling operator
We consider the acoustic isotropic wave equation parameterized in terms of
slowness with zero initial conditions assuming
the wave field does not have any energy before zero time. We define an
additional dampening term to mimic an infinite domain (see Sect. 3.2.3). At the limit of the domain,
the zero Dirichlet boundary condition is satisfied as the solution is considered to be
fully damped at the limit of the computational domain. The PDE is defined in
Eq. (2). Figure 4 demonstrates the complete setup of the acoustic wave equation with absorbing boundaries, injection of a
source function, and sampling wave fields at receiver locations. The shape of the
computational domain is hereby provided by a utility object model,
while the damping term is implemented via a
utility symbol eta defined as a Function object. It is
important to note that the discretization order of the spatial derivatives is
passed as an external parameter order and carried as metadata by the
wave field symbol u during construction, allowing the user to freely
change the underlying stencil order.

Figure 14Convection equation in Devito. In this example, the initial Dirichlet
boundary conditions are set to 1 using the API indexing feature, which allows us to assign values to the TensorFunction data.
The main (PDE) stencil expression to update the state of the wave field is
derived from the high-level wave-equation expression eqn = u.dt2 - u.laplace + damp*u.dt using SymPy utilities as demonstrated before in
Fig. 3. Additional expressions for the injection of the wave source
via the SparseFunction object src are then generated for the
forward wave field, and the source time signature is discretized onto the
computational grid via the symbolic expression src * dt**2 / m. The
weight is derived from rearranging the discretized wave
equation with a source as a right-hand side similarly to the Laplacian in
Eq. (2). A similar expression to interpolate the current state of
the wave field at the receiver locations (measurement points) is generated
through the receiver symbol. The combined list of stencils, a sum in
Python that adds the different expressions that update the wave field at
the next time step, injects the source, interpolates at the receivers, and is then
passed to the Operator constructor alongside a definition of the
spatial and temporal spacing provided by the
model utility. Devito then transforms this list of stencil expressions
into loops (inferred from the symbolic functions), replaces all necessary
constants by their values if requested, prints the generated C code, and
compiles it. The operator is finally callable in Python with
op.apply().
A more detailed explanation of the seismic setup and parameters such as the source and receiver terms in Fig. 4 is covered in Louboutin et al. (2017b).
4.3 Discrete adjoint wave equation and FWI gradient
To create the adjoint that pairs with the above forward modeling propagator we
can make use of the fact that the isotropic acoustic wave equation is
self-adjoint. This means that for the implementation of the forward wave
equation eqn, shown in Fig. 5, only the sign of the
damping term needs to be inverted, as the dampening time derivative has to be
defined in the direction of propagation (). For
the PDE stencil, however, we now rearrange the stencil expression to update the
backward wave field from the two next time steps as . Moreover, the role of the
sparse point symbols has changed (Eq. 4) so that we now inject
time-dependent data at the receiver locations (adj_src), while
sampling the wave field at the original source location (adj_rec).
Based on the definition of the adjoint operator, we can now define a similar
operator to update the gradient according to Eq. (3). As shown in
Fig. 6, we can replace the expression to sample the wave field
at the original source location with an accumulative update of the gradient
field grad via the symbolic expression Eq(grad, grad - u * v.dt2).
To compute the gradient, the forward wave field at each time step must be available, which leads to significant memory requirements. Many methods exist to tackle this memory issue, but all come with their advantages and disadvantages. For instance, we implemented optimal checkpointing with the library Revolve (Griewank and Walther, 2000) in Devito to drastically reduce the memory cost by only saving a partial time history and recomputing the forward wave field when needed (Kukreja et al., 2018). The memory reduction comes at an extra computational cost as optimal checkpointing requires log (nt)+2 extra PDE solves. Another method is boundary wave field reconstruction (McMechan, 1983; Mittet, 1994; Raknes and Weibull, 2016) that saves the wave field only at the boundary of the model, but still requires us to recompute the forward wave field during the back-propagation. This boundary method has a reduced memory cost but necessitates the computation of the forward wave field twice (one extra PDE solve), once to get the data and a second time from the boundary values to compute the gradient.
4.4 FWI using Devito operators
At this point, we have a forward propagator to model synthetic data in Fig. 4, the adjoint propagator for Eq. (4), and the FWI gradient of Eq. (3) in Fig. 6. With these three operators, we show the implementation of the FWI objective and gradient with Devito in Fig. 8. With the forward and adjoint and/or gradient operator defined for a given source, we only need to add a loop over all the source experiments and the reduction operation on the gradients (sum the gradient for each source experiment together). In practice, this loop over sources is where the main task-based or MPI-based parallelization happens. The wave-equation propagator does use some parallelization with multithreading or domain decomposition, but that parallelism requires communication. The parallelism-over-source experiment is task based and does not require any communication between the separate tasks as the gradient for each source can be computed independently and reduced to obtain the full gradient. With the complete gradient summed over the source experiments, we update the model with a simple fixed step-length gradient update (Cauchy, 1847).
This FWI function in Fig. 7 can then be included in any
black-box optimization toolbox such as SciPy optimize to solve the
inversion problem in Eq. (2). While black-box optimization methods
aim to minimize the objective, there are no guarantees that they will find a global minimum because the
objective is highly nonlinear in m and other more sophisticated methods are
required (Warner and Guasch, 2014; van Leeuwen and Herrmann, 2015; Peters and Herrmann, 2017; Witte et al., 2018).
Given the operators defined in Sect. 3 we now verify the correctness of the code generated by the Devito compiler. We first verify that the discretized wave equation satisfies the convergence properties defined by the order of discretization, and secondly we verify the correctness of the discrete adjoint and computed gradient.
Table 1Adjoint test for different discretization orders in 2-D, computed on a two-layer model in double precision. The highlighted values represent the error in the values and indicate at which decimal the error appears.

Table 2Adjoint test for different discretization orders in 3-D, computed on a two-layer model in double precision. The highlighted values indicate the error in the values and indicate at which decimal the error appears.

5.1 Numerical accuracy
The numerical accuracies of the forward modeling operator (Fig. 4) and the runtime achieved for a given spatial discretization order and grid size are compared to the analytical solution of the wave equation in constant media. We define two measures of the accuracy that compare the numerical wave field in constant velocity media to the analytical solution:
-
accuracy versus size, whereby we compare the obtained numerical accuracy as a function of the spatial sampling size (grid spacing); and
-
accuracy versus time, whereby we compare the obtained numerical accuracy as a function of runtime for a given physical model (fixed shape in physical units, variable grid spacing).
The measure of accuracy of a numerical solution relies on a hypothesis that we satisfy for these two tests:
-
the domain is large enough and the propagation time small enough to ignore boundary-related effects, i.e., the wave field never reaches the limits of the domain; and
-
the source is located on the grid and is a discrete approximation of the Dirac to avoid spatial interpolation errors. This hypothesis guarantees the existence of the analytical and numerical solution for any spatial discretization (Igel, 2016).

Figure 16Burgers' equations in Devito. In this example, we explicitly use
the FD function first_derivative. This function provides
more flexibility and allows us to take an upwind derivative, rather than a
standard centered derivative (ḋx), to avoid odd–even coupling,
which leads to chessboard artifacts in the solution.
5.1.1 Convergence in time
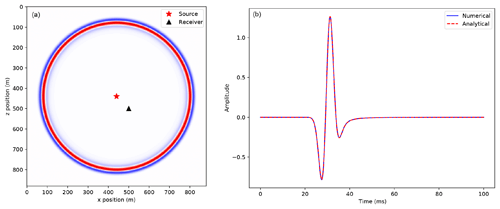
We analyze the numerical solution against the analytical solution and verify that the error between these two decreases at a second-order rate as a function of the time step size Δt. The velocity model is a 400 m×400 m domain with a source at the center. We compare the numerical solution to the analytical solution in Fig. 9.
The analytical solution is defined as (Watanabe, 2015)
where is the Hankel function of second kind and q(ω) is the spectrum of the source function. As we can see in Fig. 10 the error decreases nearly quadratically with the size of the time step with a time convergence rate slope of 1.94 in logarithmic scale that matches the theoretical expectation from a second-order temporal discretization.
5.1.2 Spatial discretization analysis
The spatial discretization analysis follows the same method as the temporal discretization analysis. We model a wave field for a fixed temporal setup with a small enough time step to ensure negligible time discretization error (dt=0.00625 ms). We vary the grid spacing (dx) and spatial discretization order and then compute the error between the numerical and analytical solution. The convergence rates should follow the theoretical rates defined in Eq. (2). In detail, for a kth-order discretization in space, the error between the numerical and analytical solution should decrease as O(dxk). The best way to look at the convergence results is to plot the error in logarithmic scale and verify that the error decreases linearly with slope k. We show the convergence results in Fig. 11. The numerical convergence rates follow the theoretical ones for every tested order with the exception of the 10th order for small grid size. This is mainly due to reaching the limits of the numerical accuracy and a value of the error on par with the temporal discretization error. This behavior for high-order and small grids is, however, in accordance with the literature as in Wang et al. (2017).
The numerical slopes obtained and displayed in Fig. 11 demonstrate that the spatial finite difference follows the theoretical errors and converges to the analytical solution at the expected rate. These two convergence results (time and space) verify the accuracy and correctness of the symbolic discretization with Devito. With this validated simulated wave field, we can now verify the implementation of the operators for inversion.
5.2 Propagators verification for inversion
We concentrate now on two tests, namely the adjoint test (or dot test) and the gradient test. The adjoint-state gradient of the objective function defined in Eq. (3) relies on the solutions of the forward and adjoint wave equations; therefore, the first mandatory property to verify is the exact derivation of the discrete adjoint wave equation. The mathematical test we use is the standard adjoint property or dot test:
The adjoint test is also individually performed on the source–receiver injection–interpolation operators in the Devito test suite. The results, summarized in Tables 1 and 2 with , verify the correct implementation of the adjoint operator for any order in both 2-D and 3-D. We observe that the discrete adjoint is accurate up to numerical precision for any order in 2-D and 3-D with an error of order . In combination with the previous numerical analysis of the forward modeling propagator that guarantees that we solve the wave equation, this result verifies that the adjoint propagator is the exact numerical adjoint of the forward propagator and that it implements the adjoint wave equation.
With the forward and adjoint propagators tested, we finally verify that the Devito operator that implements the gradient of the FWI objective function (Eq. 3, Fig. 6) is accurate with respect to the Taylor expansion of the FWI objective function. For a given velocity model and associated squared slowness m, the Taylor expansion of the FWI objective function from Eq. (2) for a model perturbation dm and a perturbation scale h is
These two equations constitute the gradient test whereby we define a small model perturbation dm and vary the value of h between 10−6 and 100 and compute the error terms:
We plot the evolution of the error terms as a function of the perturbation scale h knowing ϵ0 should be first order (linear with slope 1 in a logarithmic scale) and ϵ1 should be second order (linear with slope 2 in a logarithmic scale). We executed the gradient test defined in Eq. (5) in double precision with an eighth-order spatial discretization. The test can be run for higher orders in the same manner but since it has already been demonstrated that the adjoint is accurate for all orders, the same results would be obtained.
In Fig. 12, the matching slope of the error term with the theoretical h and h2 slopes from the Taylor expansion verifies the accuracy of the inversion operators. With all the individual parts necessary for seismic inversion, we now validate our implementation in a simple but realistic example.
5.3 Validation: full-waveform inversion
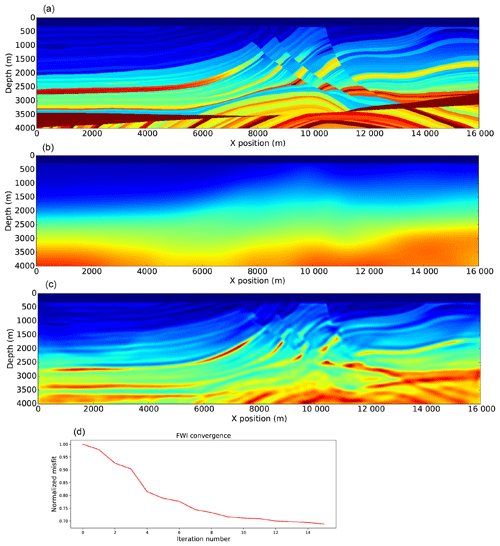
We show a simple example of FWI in Eq. (3) on the Marmousi-ii model (Versteeg, 1994). This result was obtained with the Julia interface to Devito JUDI (Witte et al., 2018, 2019) that provides high-level abstraction for optimization and linear algebra. The model size is 4 km×16 km discretized with a 10 m grid in both directions. We use a 10 Hz Ricker wavelet with 4 s recording. The receivers are placed at the ocean bottom (210 m of depth) every 10 m. We invert for the velocity with all the sources, spaced by 50 m at 10 m of depth for a total of 300 sources. The inversion algorithm used is minConf_PQN (Schmidt et al., 2009), an l-BFGS algorithm with bound constraints (minimum and maximum velocity value constraints). While conventional optimization would run the algorithm to convergence, this strategy is computationally not feasible for FWI. As each iteration requires two PDE solves per source qs (see adjoint state in Sect. 4), we can only afford 𝒪(10) iterations in practice (𝒪(104) PDE solves in total). In this example, we fix the number of function evaluations to 20, which, with the line search, corresponds to 15 iterations. The result is shown in Fig. 13 and we can see that we obtain a good reconstruction of the true model. More advanced algorithms and constraints will be necessary for more complex problems such as a less accurate initial model, noisy data, or field-recorded data (Witte et al., 2018; Peters and Herrmann, 2017); however, the wave propagator would not be impacted, making this example a good proof of concept for Devito.
This result highlights two main contributions of Devito. First, we provide PDE simulation tools that allow for the easy and efficient implementation of an inversion operator for seismic problems and potentially any PDE-constrained optimization problems. As described in Sects. 3 and 4, we can implement all the required propagators and the FWI gradient in a few lines in a concise and mathematical manner. Second, as we obtained these results with JUDI (Witte et al., 2019), a seismic inversion framework that provides a high-level linear abstraction layer on top of Devito for seismic inversion, this example illustrates that Devito is fully compatible with external languages and optimization toolboxes and allows users to use our symbolic DSL for finite differences within their own inversion framework.
5.4 Computational fluid dynamics
Finally, we describe three classical computational fluid dynamics examples to highlight the flexibility of Devito for another application domain. Additional CFD examples can be found in the Devito code repository in the form of a set of Jupyter notebooks. The three examples we describe here are the convection equation, the Burgers' equation, and the Poisson equation. These examples are adapted from Barba and Forsyth (2018), and the example repository contains both the original Python implementation with NumPy and the implementation with Devito for comparison.
5.4.1 Convection
The convection governing equation for a field u and a speed c in two dimensions is
The same way we previously described it for the wave equation, u is then
defined as a TimeFunction. In this simple case, the speed is a
constant and does not need a symbolic representation, but a more general
definition of this equation is possible with the creation of c as a Devito
Constant that can accept any runtime value. We then discretized the
PDE using forward differences in time and backward differences in space:
which is implemented in Devito as in Fig. 14.
The solution of the convection equation is displayed in Fig. 15 that shows the evolution of the field u, and the solution is consistent with the expected result produced by Barba and Forsyth (2018).
5.4.2 Burgers' equation
In this second example, we show the solution of the Burgers' equation. This example demonstrates that Devito supports coupled systems of equations and nonlinear equations easily. The Burgers' equation in two dimensions is defined as the following coupled PDE system:
where u and v are the two components of the solution and ν is the diffusion coefficient of the medium. The system of coupled equations is implemented in Devito in a few lines as shown in Fig. 16.
We show the initial state and the solution at the last time step of the Burgers' equation in Fig. 17. Once again, the solution corresponds to the reference solution of Barba and Forsyth (2018).
5.4.3 Poisson
We finally show the implementation of a solver for the Poisson equation in Devito. While the Poisson equation is not time dependent, the solution is obtained with an iterative solver and the simplest one can easily be implemented with finite differences. The Poisson equation for a field p and a right-hand side b is defined as
and its solution can be computed iteratively with
where the expression in Eq. (8) is computed until either the
number of iterations is reached (our example case) or more realistically when
. We show two different
implementations of a Poisson solver in Figs. 18 and
19. While these two implementations produce the same
result, the second one takes advantage of Devito's BufferedDimension
that allows us to iterate automatically alternating between pn and
pn+1 as the two different time buffers in the TimeFunction.
The solution of the Poisson equation is displayed in Fig. 20 with its right-hand side b.
These examples demonstrate the flexibility of Devito and show that a broad range of PDEs can easily be implemented with Devito, including a nonlinear equation, a coupled PDE system, and steady-state problems.
In this section we demonstrate the performance of Devito from a numerical and inversion point of view, as well as the absolute performance from a hardware point of view. This section only provides a brief overview of Devito's performance, and a more detailed description of the compiler and its performance is covered in Luporini et al. (2018).
6.1 Error–cost analysis
Devito's automatic code generation lets users define the spatial and temporal order of FD stencils symbolically and without having to re-implement long stencils by hand. This allows users to experiment with trade-offs between discretization errors and runtime, as higher-order FD stencils provide more accurate solutions that come at increased runtime. For our error–cost analysis, we compare absolute error in L2 norm between the numerical and the reference solution to the time to solution (the numerical and reference solution are defined in Sect. 5). Figure 21 shows the runtime and numerical error obtained for a fixed physical setup. We use the same parameter as in Sect. 5.1 with a domain of 400 m×400 m and we simulate the wave propagation for 150 ms.
The results in Fig. 21 illustrate that higher-order discretizations produce a more accurate solution on a coarser grid with a shorter runtime. This result is very useful for inverse problems, as a coarser grid requires less memory and fewer time steps. A grid size 2 times bigger implies a reduction of memory usage by a factor of 24 for 3-D modeling. Devito then allows users to design FD simulators for inversion in an optimal way, whereby the discretization order and grid size can be chosen according to the desired numerical accuracy and availability of computational resources. While a near-linear evolution of the runtime with increasing space order might be expected, we do not see such a behavior in practice. The main reason for this is that the effect of Devito's performance optimizations for different space orders is difficult to predict and does not necessarily follow a linear relationship. On top of these optimizations, the runtimes also include the source injection and receiver interpolation, which impact the runtime in a nonlinear way. Therefore, these results are still acceptable. The order of the FD stencils also affects the best possible hardware usage that can theoretically be achieved and whether an algorithm is compute or memory bound, a trade-off that is described by the roofline model.
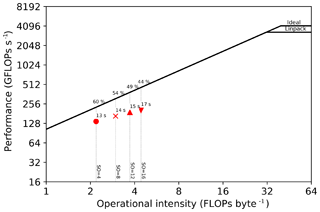
Figure 22Roofline plots for a model on a Skylake 8180 architecture. The runtimes correspond to 1000 ms of modeling for four different spatial discretization orders (4, 8, 12, 16).
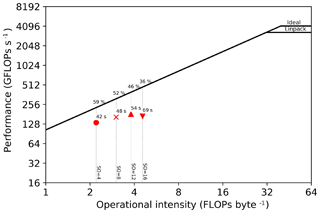
Figure 23Roofline plots for a model on a Skylake 8180 architecture. The runtimes correspond to 1000 ms of modeling for four different spatial discretization orders (4, 8, 12, 16).
6.2 Roofline analysis
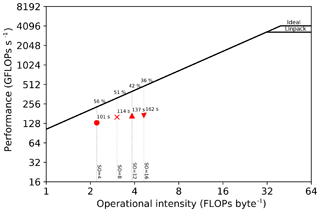
We present performance results of our solver using the roofline model, as previously discussed in Colella (2004), Asanovic et al. (2006), Patterson and Hennessy (2007), Williams et al. (2009), and Louboutin et al. (2017a). Given a finite-difference scheme, this method provides an estimate of the best achievable performance on the underlying architecture, as well as an absolute measure of the hardware usage. We also show a more classical metric, namely time to solution, in addition to the roofline plots, as both are essential for a clear picture of the achieved performance. The experiments were run on an Intel Skylake 8180 architecture (28 physical cores, 38.5 MB shared L3 cache, with cores operating at 2.5 Ghz). The observed STREAM TRIAD (McCalpin, 1991–2007) was 105 GB s−1. The maximum single-precision FLOP performance was calculated as . A (more realistic) performance peak of 3285 GFLOPs s−1 was determined by running the LINPACK benchmark (Dongarra, 1988). These values are used to construct the roofline plots. In the performance results presented in this section, the operational intensity (OI) is computed by the Devito profiler from the symbolic expression after the compiler optimization. While the theoretical OI could be used, we chose to recompute it from the final optimized symbolic stencil for a more accurate performance measure. A more detailed overview of Devito's performance model is described in Luporini et al. (2018).
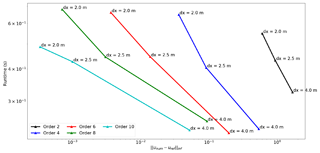
We show three different roofline plots, one plot for each domain size attempted, in Figs. 22, 23, and 24. Different space orders are represented as different data points. The time to solution in seconds is annotated next to each data point. The experiments were run with all performance optimizations enabled. Because auto-tuning is used at runtime to determine the optimal loop-blocking structure, timing only commences after auto-tuning has finished. The reported operational intensity benefits from the use of expression transformations, as described in Sect. 3; particularly relevant for this problem is the factorization of FD weights.
We observe that the time to solution increases nearly linearly with the size of the domain. For example, for a 16th-order discretization, we have a 17.1 s runtime for a domain and a 162.6 s runtime for a domain (a domain 8 times bigger and about 9 times slower). This is not surprising: the computation lies in the memory-bound regime and the working sets never fit in the L3 cache. We also note a drop in performance with a 16th-order discretization (relative to both the other space orders and the attainable peak), especially when using larger domains (Figs. 23 and 24). Our hypothesis, supported by profiling with Intel VTune (Intel Corporation, 2016), is that this is due to inefficient memory usage, in particular misaligned data accesses. Our plan to improve the performance in this regime consists of resorting to a specialized stencil optimizer such as YASK (see Sect. 7). These results show that we have a portable framework that achieves good performance on different architectures. There is small room for improvements, as the machine peak is still relatively distant, but 50 %–60 % of the attainable peak is usually considered very good. Finally, we remark that testing on new architectures will only require extensions to the Devito compiler, if any, while the application code remains unchanged.
A key motivation for developing an embedded DSL such as Devito is to enable quicker development, simpler maintenance, and better portability and performance of solvers. The other benefit of this approach is that HPC developer effort can be focused on developing the compiler technology that is reapplied to a wide range of problems. This software reuse is fundamental to keeping the pace of technological evolution. For example, one of the current projects in Devito regards the integration of YASK (Yount, 2015), a lower-level stencil optimizer conceived by Intel for Intel architectures. Adding specialized back ends such as YASK – meaning that Devito can generate and compile YASK code, rather than pure C/C++ – is the key for long-term performance portability, one of the goals that we are pursuing. Another motivation is to enable large-scale computations and as many different types of PDEs as possible. In practice, this means that a staggered grid setup with half-node discretization and domain decomposition will be required. These two main requirements to extend the DSL to a broader community and to more applications are in full development and will be made available in future releases.
We have introduced a DSL for time–domain simulation for inversion and its application to a seismic inverse problem based on the finite-difference method. Using the Devito DSL, a highly optimized and parallel finite-difference solver can be implemented within just a few lines of Python code. Although the current application focuses on features required for seismic imaging applications, Devito can already be used in problems based on other equations; a series of CFD examples is included in the code repository.
The code traditionally used to solve such problems is highly complex. The primary reason for this is that the complexity introduced by the mathematics is interleaved with the complexity introduced by the performance engineering of the code to make it useful for practical purposes. By introducing a separation of concerns, these aspects are decoupled and simplified. Devito successfully achieves this decoupling while delivering good computational performance and maintaining generality, both of which shall continue to be improved in future versions.
The asset
https://doi.org/10.5281/zenodo.1038305 (Louboutin et al., 2017c) is the official DOI for
the release of Devito 3.1.0. The source code, examples, and test script are
available on GitHub at https://github.com/opesci/devito (last access: 24 March 2019) and
contain a README for installation. A more
detailed overview of the project, with a list of publication and
documentation for the software generated with Sphinx, is available at
http://www.devitoproject.org/ (last access: 24 March 2019). To install Devito:
git clone -b v3.1.0
https://github.com/opesci/devito
cd devito
conda env create -f environment.yml
source activate devito
pip install -e .
MAL, MIL, NK, and FL designed and implemented the symbolic interface and Sympy extension in Devito.
MIL, FL, MAL, NK, and PV implemented the Devito compiler and the code generation framework.
NK and MAL implemented the checkpointing for Devito.
FJH and GJG were the PIs for the project and provided design and application input so that Devito would be usable and scalable.
PAW, MAL, and MIL developed and implemented the examples presented in this paper.
The authors declare that they have no conflict of interest.
The development of Devito was primarily supported through the Imperial
College London Intel Parallel Computing Centre. We would also like to acknowledge
support from the SINBAD II project and support from the member organizations
of the SINBAD Consortium as well as EPSRC grants EP/M011054/1 and EP/L000407/1.
Edited by: Simon Unterstrasser
Reviewed by: Jørgen Dokken and one anonymous referee
Alnæs, M. S., Logg, A., Ølgaard, K. B., Rognes, M. E., and Wells, G. N.: Unified Form Language: a domain-specific language for weak formulations of partial differential equations, ACM T. Math. Software, 40, 9, https://doi.org/10.1145/2566630, 2014. a
Andreolli, C., Thierry, P., Borges, L., Skinner, G., and Yount, C.: Chapter 23 – Characterization and Optimization Methodology Applied to Stencil Computations, in: High Performance Parallelism Pearls, edited by: Reinders, J. and Jeffers, J., 377–396, Morgan Kaufmann, Boston, https://doi.org/10.1016/B978-0-12-802118-7.00023-6, 2015. a
Arbona, A., Miñano, B., Rigo, A., Bona, C., Palenzuela, C., Artigues, A., Bona-Casas, C., and Massó, J.: Simflowny 2: An upgraded platform for scientific modeling and simulation, arXiv preprint arXiv:1702.04715, Computer Physics Communications, 229, 170–181, 2017. a
Asanović, K., Bodik, R., Catanzaro, B. C., Gebis, J. J., Husbands, P., Keutzer, K., Patterson, D. A., Plishker, W. L., Shalf, J., Williams, S. W., and Yelick, K. A.: The landscape of parallel computing research: A view from berkeley, Tech. rep., Technical Report UCB/EECS-2006-183, EECS Department, University of California, Berkeley, 2006. a
Backus, J.: The history of Fortran I, II, and III, in: History of programming languages I, ACM SIGPLAN Notices, 13, 165–180, 1978. a
Barba, L. A. and Forsyth, G. F.: CFD Python: the 12 steps to Navier-Stokes equations, Journal of Open Source Education, 9, 21, https://doi.org/10.21105/jose.00021, 2018. a, b, c
Bondhugula, U., Hartono, A., Ramanujam, J., and Sadayappan, P.: A Practical Automatic Polyhedral Parallelizer and Locality Optimizer, in: Proceedings of the 2008 ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2008, 101–113, ACM, New York, NY, USA, https://doi.org/10.1145/1375581.1375595, 2008. a, b
Cárdenas, A. F. and Karplus, W. J.: PDEL – a language for partial differential equations, Commun. ACM, 13, 184–191, 1970. a
Cauchy, A.-L.: Méthode générale pour la résolution des systèmes d'équations simultanées, Compte Rendu des Séances de L'Académie des Sciences XXV, Série A, 25, 536–538, 1847. a
Christen, M., Schenk, O., and Burkhart, H.: PATUS: A Code Generation and Autotuning Framework for Parallel Iterative Stencil Computations on Modern Microarchitectures, in: Proceedings of the 2011 IEEE International Parallel & Distributed Processing Symposium, IPDPS 2011, 676–687, IEEE Computer Society, Washington, DC, USA, https://doi.org/10.1109/IPDPS.2011.70, 2011. a
Clayton, R. and Engquist, B.: Absorbing boundary conditions for acoustic and elastic wave equations, B. Seismol. Soc. Am., 67, 1529–1540, 1977. a
Colella, P.: Defining Software Requirements for Scientific Computing, DARPA HPCS, 2004. a
Cook Jr., G. O.: ALPAL: A tool for the development of large-scale simulation codes, Tech. rep., Lawrence Livermore National Lab., CA, USA, 1988. a
Dongarra, J.: The LINPACK Benchmark: An Explanation, in: Proceedings of the 1st International Conference on Supercomputing, 456–474, Springer Verlag, London, UK, available at: http://dl.acm.org/citation.cfm?id=647970.742568 (last access: 24 March 2019), 1988. a
Farrell, P. E., Ham, D. A., Funke, S. W., and Rognes, M. E.: Automated Derivation of the Adjoint of High-Level Transient Finite Element Programs, SIAM J. Sci. Comput., 35, C369–C393, https://doi.org/10.1137/120873558, 2013. a
Fomel, S., Sava, P., Vlad, I., Liu, Y., and Bashkardin, V.: Madagascar: open-source software project for multidimensional data analysis and reproducible computational experiments, Journal of Open Research Software, 1, p.e8, https://doi.org/10.5334/jors.ag, 2013. a
Griewank, A. and Walther, A.: Algorithm 799: Revolve: An Implementation of Checkpointing for the Reverse or Adjoint Mode of Computational Differentiation, ACM Trans. Math. Softw., 26, 19–45, https://doi.org/10.1145/347837.347846, 2000. a
Haber, E., Chung, M., and Herrmann, F. J.: An effective method for parameter estimation with PDE constraints with multiple right hand sides, SIAM J. Optimiz., 22, 739–757, https://doi.org/10.1137/11081126X, 2012. a, b
Hawick, K. A. and Playne, D. P.: Simulation Software Generation using a Domain-Specific Language for Partial Differential Field Equations, in: 11th International Conference on Software Engineering Research and Practice (SERP '13), CSTN-187, p. SER3829, WorldComp, Las Vegas, USA, 2013. a
Henretty, T., Veras, R., Franchetti, F., Pouchet, L.-N., Ramanujam, J., and Sadayappan, P.: A Stencil Compiler for Short-vector SIMD Architectures, in: Proceedings of the 27th International ACM Conference on International Conference on Supercomputing, ICS '13, 13–24, ACM, New York, NY, USA, https://doi.org/10.1145/2464996.2467268, 2013. a, b, c
Hopper, G. M.: The education of a computer, in: Proceedings of the 1952 ACM national meeting (Pittsburgh), 243–249, ACM, 1952. a
Igel, H.: Computational Seismology: A Practical Introduction, Oxford University Press, 1. edn., available at: https://global.oup.com/academic/product/computational-seismology-9780198717409?cc=de&lang=en& (last access: 24 March 2019), 2016. a
Intel Corporation: Intel VTune Performance Analyzer, available at: https://software.intel.com/en-us/intel-vtune-amplifier-xe (last access: 24 March 2019), 2016. a
Iverson, K. E.: A Programming Language, John Wiley & Sons, Inc., New York, NY, USA, 1962. a
Jacobs, C. T., Jammy, S. P., and Sandham, N. D.: OpenSBLI: A framework for the automated derivation and parallel execution of finite difference solvers on a range of computer architectures, CoRR, abs/1609.01277, available at: http://arxiv.org/abs/1609.01277 (last access: 24 March 2019), 2016. a
Jones, J. L.: A survey of automatic coding techniques for digital computers, Ph.D. thesis, Massachusetts Institute of Technology, Boston, MA, USA, 1954. a
Köster, M., Leißa, R., Hack, S., Membarth, R., and Slusallek, P.: Platform-Specific Optimization and Mapping of Stencil Codes through Refinement, in: Proceedings of the 1st International Workshop on High-Performance Stencil Computations, 21 January 2014, Vienna, Austria, 1–6, 2014. a
Kukreja, N., Hückelheim, J., Lange, M., Louboutin, M., Walther, A., Funke, S. W., and Gorman, G.: High-level python abstractions for optimal checkpointing in inversion problems, arXiv preprint arXiv:1802.02474, 2018. a
Kumar, R., Wason, H., and Herrmann, F. J.: Source separation for simultaneous towed-streamer marine acquisition – a compressed sensing approach, Geophysics, 80, WD73–WD88, https://doi.org/10.1190/geo2015-0108.1, 2015. a
Lange, M., Kukreja, N., Luporini, F., Louboutin, M., Yount, C., Hückelheim, J., and Gorman, G. J.: Optimised finite difference computation from symbolic equations, in: Proceedings of the 16th Python in Science Conference (SciPy 2017), 10–16 July, Austin, Texas, edited by: Huff, K., Lippa, D., Niederhut, D., and Pacer, M., 89–96, 2017. a
Lions, J. L.: Optimal control of systems governed by partial differential equations, 1st edn., Springer Verlag, Berlin, Heidelberg, 1971. a
Liu, Y. and Fomel, S.: Seismic data interpolation beyond aliasing using regularized nonstationary autoregression, Geophysics, 76, V69–V77, https://doi.org/10.1190/geo2010-0231.1, 2011. a
Logg, A., Mardal, K.-A., Wells, and Wells, G.: Automated Solution of Differential Equations by the Finite Element Method, The FEniCS Book, Springer, https://doi.org/10.1007/978-3-642-23099-8, 2012. a, b, c
Louboutin, M., Lange, M., Herrmann, F. J., Kukreja, N., and Gorman, G.: Performance prediction of finite-difference solvers for different computer architectures, Comput. Geosci., 105, 148–157, https://doi.org/10.1016/j.cageo.2017.04.014, 2017a. a, b
Louboutin, M., Witte, P., Lange, M., Kukreja, N., Luporini, F., Gorman, G., and Herrmann, F. J.: Full-waveform inversion, Part 1: Forward modeling, The Leading Edge, 36, 1033–1036, https://doi.org/10.1190/tle36121033.1, 2017b. a
Louboutin, M., Luporini, F., Lange, M., Kukreja, N., Pandolfo, V., Kazakas, P., Zhang, S., Gorman, G., Hueckelheim, J., Peng, P., Velesko, P., and McCormick, D.: opesci/devito: Devito-3.1, https://doi.org/10.5281/zenodo.1038305, 2017. a
Luporini, F., Varbanescu, A. L., Rathgeber, F., Bercea, G.-T., Ramanujam, J., Ham, D. A., and Kelly, P. H. J.: Cross-Loop Optimization of Arithmetic Intensity for Finite Element Local Assembly, ACM Trans. Archit. Code Optim., 11, 57:1–57:25, https://doi.org/10.1145/2687415, 2015. a
Luporini, F., Lange, M., Louboutin, M., Kukreja, N., Hückelheim, J., Yount, C., Witte, P., Kelly, P. H. J., Gorman, G. J., and Herrmann, F. J.: Architecture and performance of Devito, a system for automated stencil computation, CoRR, abs/1807.03032, available at: http://arxiv.org/abs/1807.03032 (last access: 24 March 2019), 2018. a, b, c, d
McCalpin, J. D.: STREAM: Sustainable Memory Bandwidth in High Performance Computers, Tech. rep., University of Virginia, Charlottesville, Virginia, available at: http://www.cs.virginia.edu/stream/ (last access: 24 March 2019), a continually updated technical report, 1991–2007. a
McMechan, G. A.: Migration by extrapolation of time-dependent boundary values, Geophys. Prospect., 31, 413–420, https://doi.org/10.1111/j.1365-2478.1983.tb01060.x, 1983. a
Membarth, R., Hannig, F., Teich, J., and Köstler, H.: Towards domain-specific computing for stencil codes in HPC, in: High Performance Computing, Networking, Storage and Analysis (SCC), Salt Lake City, UT, 2012 SC Companion, IEEE, 1133–1138, https://doi.org/10.1109/SC.Companion.2012.136, 2012. a
Meurer, A., Smith, C. P., Paprocki, M., Čertík, O., Kirpichev, S. B., Rocklin, M., Kumar, A., Ivanov, S., Moore, J. K., Singh, S., Rathnayake, T., Vig, S., Granger, B. E., Muller, R. P., Bonazzi, F., Gupta, H., Vats, S., Johansson, F., Pedregosa, F., Curry, M. J., Terrel, A. R., Roučka, V., Saboo, A., Fernando, I., Kulal, S., Cimrman, R., and Scopatz, A.: SymPy: symbolic computing in Python, PeerJ Computer Science, 3, e103, https://doi.org/10.7717/peerj-cs.103, 2017. a
Mittet, R.: Implementation of the Kirchhoff integral for elastic waves in staggered-grid modeling schemes, Geophysics, 59, 1894–1901, https://doi.org/10.1190/1.1443576, 1994. a
Naghizadeh, M. and Sacchi, M. D.: f-x adaptive seismic-trace interpolation, Geophysics, 74, V9–V16, https://doi.org/10.1190/1.3008547, 2009. a
Osuna, C., Fuhrer, O., Gysi, T., and Bianco, M.: STELLA: A domain-specific language for stencil methods on structured grids, in: Poster Presentation at the Platform for Advanced Scientific Computing (PASC) Conference, Zurich, Switzerland, 2014. a
Patterson, D. A. and Hennessy, J. L.: Computer Organization and Design: The Hardware/Software Interface, 3rd edn., Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 2007. a
Peters, B. and Herrmann, F. J.: Constraints versus penalties for edge-preserving full-waveform inversion, The Leading Edge, 36, 94–100, https://doi.org/10.1190/tle36010094.1, 2017. a, b
Plessix, R.-E.: A review of the adjoint-state method for computing the gradient of a functional with geophysical applications, Geophys. J. Int., 167, 495–503, https://doi.org/10.1111/j.1365-246X.2006.02978.x, 2006. a
Raknes, E. B. and Weibull, W.: Efficient 3D elastic full-waveform inversion using wavefield reconstruction methods, Geophysics, 81, R45–R55, https://doi.org/10.1190/geo2015-0185.1, 2016. a
Rathgeber, F., Ham, D. A., Mitchell, L., Lange, M., Luporini, F., McRae, A. T. T., Bercea, G., Markall, G. R., and Kelly, P. H. J.: Firedrake: automating the finite element method by composing abstractions, CoRR, abs/1501.01809, available at: http://arxiv.org/abs/1501.01809 (last access: 24 March 2019), 2015. a, b, c
Schmidt, M., van den Berg, E., Friedlander, M. P., and Murphy, K.: Optimizing Costly Functions with Simple Constraints: A Limited-Memory Projected Quasi-Newton Algorithm, in: Proceedings of The Twelfth International Conference on Artificial Intelligence and Statistics (AISTATS) 2009, edited by: van Dyk, D. and Welling, M., vol. 5, 456–463, Clearwater Beach, Florida, 2009. a
Seongjai Kim, H. L.: High-order schemes for acoustic waveform simulation, Appl. Numer. Math., 57, 402–414, 2007. a
Sun, D. and Symes, W. W.: IWAVE implementation of adjoint state method, Tech. Rep. 10-06, Department of Computational and Applied Mathematics, Rice University, Houston, Texas, USA, available at: https://pdfs.semanticscholar.org/6c17/cfe41b76f6b745c435891ea\%6ba6f4e2c2dbf.pdf (last access: 24 March 2019), 2010. a
Symes, W. W.: Acoustic Staggered Grid Modeling in IWAVE, The Rice Inversion Project, p. 141, available at: http://www.trip.caam.rice.edu/reports/2014/book.pdf#page=145 (last access: 24 March 2019), 2015a. a, b
Symes, W. W.: IWAVE structure and basic use cases, The Rice Inversion Project, p. 85, available at: http://www.trip.caam.rice.edu/reports/2014/book.pdf#page=89 (last access: 24 March 2019), 2015b. a
Symes, W. W., Sun, D., and Enriquez, M.: From modelling to inversion: designing a well-adapted simulator, Geophys. Prospect., 59, 814–833, https://doi.org/10.1111/j.1365-2478.2011.00977.x, 2011. a
Tang, Y., Chowdhury, R. A., Kuszmaul, B. C., Luk, C.-K., and Leiserson, C. E.: The pochoir stencil compiler, in: Proceedings of the twenty-third annual ACM symposium on Parallelism in algorithms and architectures, 117–128, ACM, San Jose, CA, USA, 2011. a, b
Tarantola, A.: Inversion of seismic reflection data in the acoustic approximation, Geophysics, 49, 1259, 1140–1395, https://doi.org/10.1190/1.1441754, 1984. a
Umetani, Y.: DEQSOL A numerical Simulation Language for Vector/Parallel Processors, Proc. IFIP TC2/WG22, in: Parallel Processing for Scientific Computing, 5, 147–164, 1985. a
Unat, D., Cai, X., and Baden, S. B.: Mint: realizing CUDA performance in 3-D stencil methods with annotated C, in: ICS '11 International Conference on Supercomputing, Tucson, AZ, USA, 214–224, ACM, New York, NY, USA, 2011. a
Van Engelen, R., Wolters, L., and Cats, G.: Ctadel: A generator of multi-platform high performance codes for pde-based scientific applications, in: ICS '96 Proceedings of the 10th international conference on Supercomputing, 86–93, ACM, Philadelphia, Pennsylvania, USA, 1996. a
van Leeuwen, T. and Herrmann, F. J.: A penalty method for PDE-constrained optimization in inverse problems, Inverse Probl., 32, 015007, https://doi.org/10.1088/0266-5611/32/1/015007, 2015. a
Versteeg, R.: The Marmousi experience; velocity model determination on a synthetic complex data set, The Leading Edge, 13, 927–936, 1994. a
Virieux, J.: P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method, Geophysics, 51, 889–901, https://doi.org/10.1190/1.1442147, 1986. a
Virieux, J. and Operto, S.: An overview of full-waveform inversion in exploration geophysics, Geophysics, 74, WCC1–WCC26, https://doi.org/10.1190/1.3238367, 2009. a
Wang, S., Nissen, A., and Kreiss, G.: Convergence of finite difference methods for the wave equation in two space dimensions, Computing Research Repository, available at: https://arxiv.org/abs/1702.01383 (last access: 24 March 2019), 2017. a
Warner, M. and Guasch, L.: Adaptive waveform inversion: Theory, 1089–1093, https://doi.org/10.1190/segam2014-0371.1, SEG 2014, Denver, Colorado, 2014. a
Wason, H., Oghenekohwo, F., and Herrmann, F. J.: Low-cost time-lapse seismic with distributed compressive sensing – Part 2: impact on repeatability, Geophysics, 82, P15–P30, https://doi.org/10.1190/geo2016-0252.1, 2017. a
Watanabe, K.: Green's Functions for Laplace and Wave Equations, pp. 33–76, Springer International Publishing, Cham, https://doi.org/10.1007/978-3-319-17455-6_2, 2015. a
Weiss, R. M. and Shragge, J.: Solving 3D anisotropic elastic wave equations on parallel GPU devices., Geophysics, 78, 1Ma-Z51, https://doi.org/10.1190/geo2012-0063.1, 2013. a
Williams, S., Waterman, A., and Patterson, D.: The Roofline model offers insight on how to improve the performance of software and hardware, Communications of the ACM – A Direct Path to Dependable Software CACM Homepage archive, 52, 65–76, 2009. a
Witte, P., Louboutin, M., Lensink, K., Lange, M., Kukreja, N., Luporini, F., Gorman, G., and Herrmann, F. J.: Full-waveform inversion, Part 3: Optimization, The Leading Edge, 37, 142–145, https://doi.org/10.1190/tle37020142.1, 2018. a, b, c
Witte, P. A., Louboutin, M., Kukreja, N., Luporini, F., Lange, M., Gorman, G. J., and Herrmann, F. J.: A large-scale framework for symbolic implementations of seismic inversion algorithms in Julia, available at: https://www.slim.eos.ubc.ca/Publications/Private/Submitted/20\%18/witte2018alf/witte2018alf.html (last access: 24 March 2019), Geophysics, 84, F57–F71, https://doi.org/10.1190/geo2018-0174.1, 2019. a, b
Yount, C.: Vector Folding: Improving Stencil Performance via Multi-dimensional SIMD-vector Representation, in: 2015 IEEE 17th International Conference on High Performance Computing and Communications, 2015 IEEE 7th International Symposium on Cyberspace Safety and Security, and 2015 IEEE 12th International Conference on Embedded Software and Systems, 24–26 August 2015, 865–870, https://doi.org/10.1109/HPCC-CSS-ICESS.2015.27, 2015. a, b, c, d
Zhang, Y. and Mueller, F.: Auto-generation and Auto-tuning of 3D Stencil Codes on GPU Clusters, in: Proceedings of the Tenth International Symposium on Code Generation and Optimization, CGO '12, 155–164, ACM, New York, NY, USA, https://doi.org/10.1145/2259016.2259037, 2012. a