the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Implementation of the sectional aerosol module SALSA2.0 into the PALM model system 6.0: model development and first evaluation
Antti Hellsten
Pontus Roldin
Harri Kokkola
Juha Tonttila
Mikko Auvinen
Christoph Kent
Prashant Kumar
Björn Maronga
Leena Järvi
Urban pedestrian-level air quality is a result of an interplay between turbulent dispersion conditions, background concentrations, and heterogeneous local emissions of air pollutants and their transformation processes. Still, the complexity of these interactions cannot be resolved by the commonly used air quality models. By embedding the sectional aerosol module SALSA2.0 into the large-eddy simulation model PALM, a novel, high-resolution, urban aerosol modelling framework has been developed. The first model evaluation study on the vertical variation of aerosol number concentration and size distribution in a simple street canyon without vegetation in Cambridge, UK, shows good agreement with measurements, with simulated values mainly within a factor of 2 of observations. Dispersion conditions and local emissions govern the pedestrian-level aerosol number concentrations. Out of different aerosol processes, dry deposition is shown to decrease the total number concentration by over 20 %, while condensation and dissolutional increase the total mass by over 10 %. Following the model development, the application of PALM can be extended to local- and neighbourhood-scale air pollution and aerosol studies that require a detailed solution of the ambient flow field.
- Article
(6942 KB) -
Supplement
(1686 KB) - BibTeX
- EndNote
The coincidence of rising population densities, high air pollutant emissions, and limited ventilation in urban areas leads to an increasing number of air-pollution-related health problems and premature deaths globally every year (Gakidou et al., 2017; WHO, 2016). The local air quality is an outcome of complex interactions between the urban landscape, meteorology, background pollutant concentrations, and local emissions, as well as the chemical and physical processes of air pollutants. Thereby, urban air pollutant concentration fields are highly irregular in both time and space (e.g. Kumar et al., 2011). At the same time, pollutant characteristics, such as the size of aerosol particles and the chemical compositions of both particles and gaseous mixtures, are essential factors in determining health impacts (for review, see, e.g. Kelly and Fussell, 2012). Traditionally used local urban air quality models, such as Gaussian dispersion or semi-empirical street pollution models, cannot resolve these details in concentration fields and interactions due to an inadequate representation of urban complexity and limitations in resolving any fine-scale flow structures (Tominaga and Stathopoulos, 2016).
Detailed information on the variability of urban air pollutant concentrations are, however, highly valuable to urban planning to design healthy living environments (Giles-Corti et al., 2016; Kurppa et al., 2018), to air quality monitoring network design, and to conducting exposure studies. Therefore, a building-resolving tool for simulating and predicting air quality in real complex urban environments in current and future conditions is needed. To determine airflow and dispersion, computational fluid dynamics (CFDs) models, notably large-eddy simulation (LES), are currently the most promising methods. Compared to LES, turbulence models based on Reynolds-averaged Navies–Stokes (RANS) equations can be computationally less demanding, but their ability to resolve instantaneous turbulence structures above a complex urban surface is shown to be clearly weaker (e.g. Antoniou et al., 2017; García-Sánchez et al., 2018, and references within). With either method, the computational costs have been the bottleneck in extending CFD-based air quality modelling from tailpipe emission studies (e.g. Huang et al., 2014; Liu et al., 2011) to neighbourhood-scale studies. Fortunately, constantly increasing computational power has already allowed urban LES modelling for entire neighbourhoods up to 1 day or even more in a supercomputing environment (e.g. Resler et al., 2017). Currently, there are a number of RANS and LES models coupled with some chemical mechanism (Zhong et al., 2016) and a few RANS models with an aerosol module, for instance Mercure_Saturne with MAM (Albriet et al., 2010) and ANSYS-Fluent-based models (Uhrner et al., 2007; Huang et al., 2014) such as CTAG (Wang and Zhang, 2012). There is also at least one LES model including a detailed aerosol module (Liu et al., 2011), which, however, is only applied in a tailpipe emission study. The CTAG model has also been run in an LES mode (Steffens et al., 2013), but to date aerosol simulations have only considered dry deposition (Tong et al., 2016a, b) and chemical composition has been usually ignored.
The fate of aerosol particles in the atmosphere substantially depends on their size distribution. Consequently, detailed aerosol modelling requires size-specific emission and background information as input. Estimates for background aerosol size distributions and concentrations can be attained from larger-scale models, whereas emission data are usually treated as total aerosol mass. Hence, emission size distribution has to be estimated based on the source type and vehicle fleet in the case of traffic emissions. If any important emission source is neglected, aerosol processes are also calculated erroneously. At the same time, as LES outperforms traditionally used urban air quality models in resolving the turbulent wind field and pollutant dispersion, LES-based air quality models produce unique information on pollutant transformation and dispersion processes with accurate emission estimates.
Numerical approaches to describe the aerosol size distribution and to solve the aerosol general dynamic equations can generally be divided into modal, moment, and sectional approaches. Modal aerosol modules (Ackermann et al., 1998; Liu et al., 2012; Vignati et al., 2004) represent the continuous aerosol size distribution as a superposition of several modes (usually log-normal distributions), whereas moment-based methods track the lower-order radial moments of the aerosol size distribution (McGraw, 1997). Both approaches are computationally efficient due to the small number of prognostic variables. However, the modal approach lacks accuracy in simulating the evolution of the aerosol size distribution, especially if the standard deviations of log-normal modes are not allowed to vary (Whitby and McMurry, 1997; Zhang et al., 1999). Applying the moment approach instead requires resolving a closure problem of the moment evolution equations (Wright et al., 2001). Furthermore, as aerosol properties are tied into moments, which are typically not observed properties except for the first moments, retrieving information on aerosol properties during the simulation increases the computational load. In the sectional approach (Gong et al., 2003; Zaveri et al., 2008; Zhang et al., 2004), the aerosol size distribution is represented as a discrete set of size bins. The sectional approach is flexible and accurate, but it is usually more computationally demanding due to the high number of prognostic variables.
To meet the needs of a high-resolution urban air quality model that can account for the complex interactions controlling the local air quality at the neighbourhood to city scale, this article presents the implementation of the aerosol module SALSA2.0 (Sectional Aerosol Module for Large Scale Applications; Kokkola et al., 2008, 2018) as a part of the PALM model system (see Maronga et al., 2015, for a description of PALM 4.0; a description of version 6.0 is envisaged in this special issue of Geoscientific Model Development). The aim is to include aerosol dynamic processes into PALM, evaluate the model performance under different wind conditions, and study the relative impact of aerosol processes on the aerosol size distribution and chemical composition in real urban environment.
The modelling methods and equations of SALSA2.0, implementation into PALM, computational costs, and inevitable numerical issues related to the sectional representation are discussed in Sect. 2. The model evaluation set-up and sensitivity tests are described in Sect. 3 and the results of the model simulations in Sect. 4. Finally, Sect. 5 discusses the applications and limitations of the model.
2.1 PALM
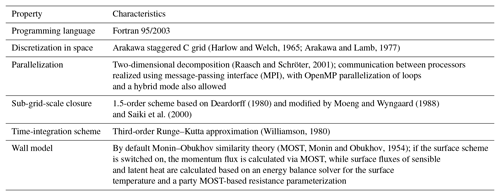
The PALM model system (version 6.0) features an LES core for atmospheric and oceanic boundary layer flows, which solves the non-hydrostatic, filtered, incompressible Navier–Stokes equations of wind (u, v, and w) and scalar variables (sub-grid-scale turbulent kinetic energy e, potential temperature θ, and specific humidity q) in Boussinesq-approximated form. Note that PALM, originally developed as a pure LES code, now also offers a RANS-type turbulence parameterization. PALM is especially suitable for complex urban areas owing to features such as a Cartesian topography scheme, a plant canopy module, and recent model enhancements like the so-called PALM-4U (short for PALM for urban applications) components, including an urban surface scheme (first version described in Resler et al., 2017) and a land surface scheme (first description in Maronga and Bosveld, 2017). Furthermore, other PALM-4U components, such as chemistry and indoor climate modules, have been or are currently being implemented into the PALM model system to develop a modern and highly efficient urban climate model (Maronga et al., 2019). Due to its excellent scalability on massively parallel computer architectures (up to 50 000 processor cores; Maronga et al., 2015), PALM is applicable for carrying out computationally expensive simulations over large, neighbourhood-scale, and city-scale domains with a sufficiently high grid resolution for urban LES (Auvinen et al., 2017; Xie and Castro, 2006). The performance of PALM over urban-like surfaces has been successfully evaluated against wind tunnel simulations, previous LES studies, and field measurements (Kanda et al., 2013; Letzel et al., 2008; Park et al., 2015; Razak et al., 2013). Some fundamental technical specifications of PALM are represented in Table 1.
(Harlow and Welch, 1965; Arakawa and Lamb, 1977)(Raasch and Schröter, 2001)Deardorff (1980)Moeng and Wyngaard (1988)Saiki et al. (2000)(Williamson, 1980)(MOST, Monin and Obukhov, 1954)2.2 SALSA
SALSA2.0 (referred to hereafter simply as SALSA) was selected as the basis for representing aerosol dynamics in PALM since one major criterion in its development has been limiting computational expenses without the cost of accuracy. A major share of the expenses stem from having a large number of prognostic variables to describe the aerosol population. SALSA has been optimized for resolving aerosol microphysics in a very large number of grid points, such as in global-scale climate models. Nonetheless, the same aerosol processes and model design choices are relevant at local scale.
In SALSA, the aerosol number size distribution is discretized into XB size bins i based on the mean dry particle diameter of each bin. The number ni (m−3) and mass concentration mc, i (kg m−3) of each chemical component c are the model prognostic variables. SALSA was originally optimized for computationally expensive large-scale climate models, and therefore the number of size bins is kept to a minimum (default XB=10) and only the following chemical components can currently be included: sulfuric acid (H2SO4), organic carbon (OC), black carbon (BC), nitric acid (HNO3), ammonium (NH3), sea salt, dust, and water (H2O). Furthermore, the gaseous concentrations of H2SO4, HNO3, NH3, and semi- and non-volatile organics (SVOCs and NVOCs) that can condense or dissolve on aerosol particles are also default prognostic variables. Nitrates and ammonium were not included in the original SALSA but have later been added (Kudzotsa et al., 2019). The sectional size distribution can be further divided into subranges 1 ( nm) and 2 ( nm). Subrange 1 consists of the smallest particles assumed to be internally mixed, strongly hygroscopic, and containing only H2SO4, OC, HNO3, and/or NH3. Subrange 2 can contain all chemical components and it can be further divided into strongly hygroscopic (2a) and weakly hygroscopic (2b) subranges to allow for the description of externally mixed aerosol particle populations (Kokkola et al., 2018). The evolution of aerosol size distribution is represented using the sectional hybrid-bin method (Young, 1974; Chen and Lamb, 1994). As a difference to the original SALSA, is calculated as the geometric mean diameter instead of the arithmetic mean. Assuming spherical particles, the latter tends to overestimate the total volume , especially for larger aerosol particles when XB∼10.
The original SALSA contains detailed descriptions for the aerosol dynamic processes of nucleation, condensation, dissolutional growth, and coagulation, and here it has been further extended by including dry deposition on solid surfaces and resolved-scale vegetation and gravitational settling. The process of particle resuspension from surfaces is currently neglected. However, the resuspension of road dust, for example, can be included in the model as an additional surface emission (see Sect. 2.2.5).
A detailed description of the aerosol source–sink terms is given below (and in Kokkola et al., 2008 and Tonttila et al., 2017).
2.2.1 Coagulation
Coagulation decreases the aerosol number as two aerosol particles collide to form one larger particle. In SALSA, coagulation is solved using the non-iterative method by Jacobson (2005). For ni,
and, similarly, for mc, i,
Here, t and t−Δt are the current and previous time steps, βi, j is the coagulation kernel (m3 s−1) of the colliding aerosol particles in size bins i and j, υc, i is the aerosol volume concentration of chemical component c in size bin i, and ρc is its density. The coagulation kernel is the product of a collision kernel Ki, j (m3 s−1) and a dimensionless coalescence efficiency . For aerosol particles smaller than 2 µm in radius, can be approximated as unity (i.e. particles stick together) as the likelihood of bounce-off is low (Beard and Ochs, 1984). Brownian coagulation is assumed for aerosol particles, for which Ki, j in the transition regime is calculated with the interpolation formula by Fuchs (1964):
where ri (m) is the particle radius, Γp, i (m2 s−1) is the particle diffusion coefficient, δi (m) is the mean distance from the centre of the sphere reached by particles leaving the surface of the sphere and travelling a distance of particle mean free path, and vp, i (m s−1) is the thermal speed of a particle in air.
2.2.2 Condensation and dissolutional growth
The condensation of gases on an aerosol particle increases the particle volume and decreases the gas-phase concentrations. For water vapour, H2SO4, NVOC, and SVOC condensation is calculated by applying the analytical predictor of a condensation scheme (Jacobson, 2005) in which the vapour mole concentration Cc,t at time step t after condensation is first calculated as
where is the particle volume-dependent mass-transfer coefficient (s−1) in size bin i at the previous time step t−Δt, is the equilibrium saturation ratio, and is an uncorrected saturation vapour mole concentration (mol m−3) of the condensing gas c. The change in particle mole concentration in the aerosol size bin i is then given by the formula
which is then translated to aerosol number and mass concentrations. The condensation and evaporation of water vapour on aerosol particles would require a very short time step to avoid non-oscillatory solutions. The applied solution used in SALSA is described in Tonttila et al. (2017).
Furthermore, aerosol particles may grow further due to dissolutional growth when a gas transfers to a particle surface and dissolves in liquid water on the surface. This partitioning between the gaseous and particulate phases is solved for water vapour, nitric acid, and ammonia using the analytical predictor of dissolution (APD) scheme (Jacobson, 2005) in the following way. First, the vapour mole concentration Cc, t after dissolutional growth at time step t is calculated as
Here, is the dimensionless Henry's constant for chemical compound c in size bin i:
where mv (mol m−3) is the molecular weight of water, cw, i (mol m−3) is the mole concentration of liquid water in aerosol size bin i, m3 atm K−1 mol−1 is the universal gas constant, T (K) is the ambient temperature, and Hc (mol kg−1 atm−1) is the Henry's law constant estimated by the thermodynamic model PD-FiTE (Topping et al., 2009). Finally, the new particle mole concentration is given by
which is then translated to number and mass concentrations. The evaporation of gases from aerosol particle surfaces, with water being an exception, is not considered.
2.2.3 Dry deposition and gravitational settling
Dry deposition removes aerosol particles from air when they collide with a surface and stick to it. Here, the original scheme in SALSA allowing dry deposition on horizontal surfaces was extended by also including deposition on vertical solid surfaces (e.g. building walls) and resolved-scale vegetation. Deposition on sub-grid vegetation (e.g. grass surface) is not yet implemented. By default, dry deposition velocity vd (m s−1) is calculated by applying the size-segregated scheme by Zhang et al. (2001) (hereafter Z01), which is the most applied dry deposition scheme in numerical studies. For size bin i,
where ρp and ρa are the particle and air densities (kg m−3), g (m s−2) is the gravitational acceleration, Gi is the Cunningham slip-correction factor, ηa (kg m−1 s−1) is the dynamic viscosity of air, ϵ0=3 and β=2 are empirical constants, u* (m s−1) is the friction velocity of above a surface, Sti is the Stokes number, Sci is the particle Schmidt number, γ and α are empirical constants that depend on the surface type, and A is the characteristic radius of the different surface types and seasonal categories. Note that the aerodynamic resistance in the original Z01 formulation is not considered here as LES resolves the aerodynamic effect explicitly. For solid surfaces, u* is solved within PALM by applying a stability-adjusted logarithmic wind profile, whereas for the resolved-scale vegetation an estimation (Prandtl, 1925), where CD is the canopy drag coefficient and is the three-dimensional wind speed, is applied. Z01 has been suggested to overestimate vd for submicron particles (Petroff and Zhang, 2010; Mingxuan et al., 2018), and therefore as an alternative to Z01, the formulation by Petroff and Zhang (2010) (hereafter P10) for the deposition velocity can be used (see Sect. S1 in the Supplement). The different parameterizations Z01 and P10 for vd over built surfaces and deciduous broadleaf trees during leaf-on period are visualized in Fig. 1.
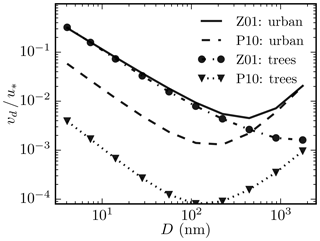
Figure 1Normalized deposition velocity as a function of aerosol particle diameter D (nm) for urban surfaces (solid and dashed lines) and deciduous broadleaf trees (dashed–dotted line with circles and dotted line with triangles) using the parameterization by Zhang et al. (Z01, 2001) and Petroff and Zhang (P10, 2010).
Dry deposition on vegetation creates a local sink term,
which depends on the local leaf area density (LAD), whereas dry deposition on horizontal surfaces and building walls is implemented by means of surfaces fluxes:
The same equations apply for mc, i. When not in contact with a surface, only gravitational settling contributes to dry deposition and generates a downward flux of particles, which is mainly important for large particles (D>1.0 µm) (Zhang et al., 2001; Petroff and Zhang, 2010). Dry deposition and gravitational settling are currently calculated only for aerosol particles and not for gaseous components.
2.2.4 New particle formation
In the model evaluation represented here, nucleation is assumed to have already occurred (Rönkkö et al., 2007; Uhrner et al., 2007), and the nucleation-mode aerosol particles are given to the model as an input. That notwithstanding, new particle formation by sulfuric acid can be taken into account by calculating the apparent rate of formation of 3 nm sized aerosol particles according to the parameterization by Kerminen and Kulmala (2002), Lehtinen et al. (2007), or Anttila et al. (2010). To calculate the “real” nucleation rate, users can choose between the binary (Vehkamäki et al., 2002), ternary (Napari et al., 2002a, b), kinetic (Sihto et al., 2006; Riipinen et al., 2007), or activation-type (Riipinen et al., 2007) nucleation.
2.2.5 Emissions
Aerosol particle emissions can be given to the model as an input by applying three levels of detail (LOD): parameterized (LOD1, units kg m−2 s−1) or detailed (LOD2, units m−2 s−1) two-dimensional surface fluxes or three-dimensional sources (LOD3, units m−3 s−1). Using LOD1, aerosol emissions are given as particulate mass (PM) emissions, from which the size-segregated number emissions are calculated within the model implementing default aerosol size distributions and mass compositions for each emission category EC (e.g. traffic, domestic heating, etc.). LOD2 and LOD3 emission data include and the mass composition per each EC, based on which the mass emission per size bin i and chemical component c are then calculated within the model. Gaseous emissions can be specified using any LOD. The time dependency of the aerosol emissions has not been implemented yet.
2.3 Model coupling and steering
SALSA is integrated into PALM as an optional PALM-4U module, which directly utilizes the momentum and scalar concentration fields of the parent model as input. The aerosol source–sink terms are resolved sequentially at a user-specified frequency fSALSA, while the prognostic equations and thus the transport of aerosol number and mass as well as gas concentrations are resolved at every LES time step ΔtLES in PALM. Molecular diffusion is assumed negligible compared with turbulent diffusion and is thus ignored.
Since water is a default chemical component in SALSA, PALM needs to be run in the humid mode (i.e. calculate the prognostic equation for specific humidity q). The particle water content per size bin i can be represented either as a prognostic variable or as a diagnostic variable and calculated at each ΔtSALSA based on the equilibrium solution using the Zdanovskii–Stokes–Robinson (ZSR) method (Stokes and Robinson, 1966). The feedback on temperature and humidity due to the condensation of water vapour on particles can be switched off. Moreover, SALSA can be run together with the available PALM-4U chemistry module to transfer the gas concentrations, while the impact of aerosol particles on radiative transfer has not been implemented yet.
2.4 Computational expenses
Each ni, mc,i, and gaseous compound introduces a new prognostic variable that is transported by the flow in PALM. Increasing the number of prognostic variables XPV from the default value of XPV=6 (wind components u, v, w and scalars e, θ, and q) to
where XB is the number of size bins, XCC the total number of chemical components (aerosol phase), and XG=5 the total number of gaseous compounds, increases the computational load tremendously. To estimate the increase in computational costs caused by significantly increasing XPV, and also resolving the aerosol dynamics, simulations over a simple test domain of (see Fig. S1 in the Supplement) were conducted with varying set-ups for SALSA.
Table 2The relative change in the total computational time over a modelling domain with different configurations for SALSA. The number of simulated size bins XB=10, time step of the LES model Δt≈2 s, and the total simulation time 1000 s. XCC stands for the number of chemical components and ΔXPV for the change in the number of prognostic variables.
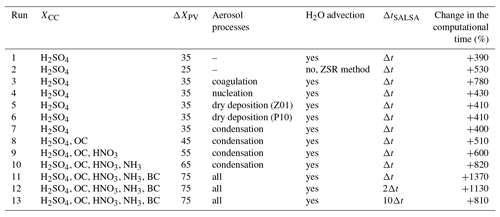
The relative changes in computational load per simulation are given in Table 2. Adding XB=10 size bins composed of XCC=2 chemical components (water always present) introduces ΔXPV=35 new prognostic variables and increases the original computational time by nearly a factor of 4 (run 1). Calculating the aerosol water content at each ΔtSALSA instead of treating it as a prognostic variable is even more demanding (run 2). Of all aerosol dynamic processes, coagulation is the most expensive (run 3). Including more chemical components further increases the computational time (runs 8–13), which can be notably decreased by lengthening ΔtSALSA (runs 12–13). Considering the longer timescales of aerosol dynamic processes compared to dispersion (e.g. Pryor and Binkowski, 2004; Kumar et al., 2008), ΔtSALSA=10Δt is considered to be reasonable in urban simulations with a grid resolution of ∼1 m and Δt∼0.1. In any case, the computational expenses are multiplied when SALSA is included, which limits the size of LES model domains to be considered.
2.5 Initialization of the aerosol number and mass size distribution
The initial aerosol size distribution is defined by setting the number concentration of particles in each bin ni of which the volume υc, i and mass concentrations mc, i are calculated based on the geometric mean diameter . Aerosol emissions are defined similarly. In other words, the total number concentration is preserved in the initialization, whereas uncertainties arise when estimating mc, i or vc, i.
Limiting XB in a sectional aerosol module is a simple method to reduce computational costs and memory demand. However, this results in an inevitable loss of accuracy as the aerosol size range covers many orders of magnitude from a few nanometres to several micrometres. To test the sensitivity of the representation of the aerosol number and mass size distribution to XB, four different configurations are tested (Fig. 2). All configurations cover particles from 3 nm to 2.5 µm, and subrange 1 includes particles up to 10 nm. The default configuration contains XB=10 with two bins in subrange 1. The second configuration contains XB=8 and only one bin in subrange 1, whereas the third configuration contains two additional bins in subrange 2 compared to the default configuration. Additionally, an ideal configuration with XB=50 was tested.
The total aerosol particle volume concentration V is highly sensitive to XB, and the rate of overestimation increases with decreasing XB (Fig. 2). Overestimating particle volume causes errors in, for instance, calculating the coagulation kernel, gas-to-particle mass transfer, and deposition velocity. Furthermore, the ability of a sectional module to capture narrow features in a size distribution (e.g. in Fig. 2c) improves with higher XB. To compromise between computational costs and modelling accuracy, XB=10 is used in this evaluation study.
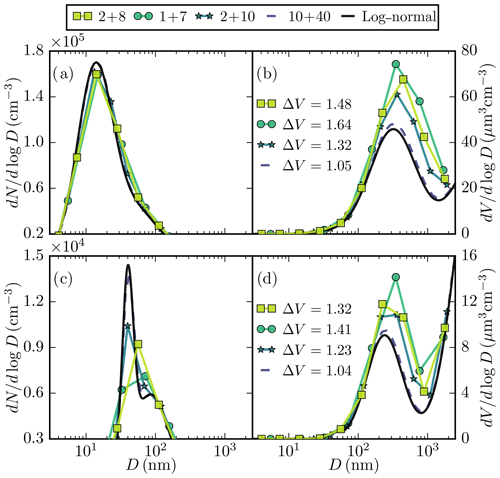
Figure 2A sectional representation of the aerosol number dN∕dlog D (cm−3) (a, c) and volume dV∕dlog D (µm3 cm−3) (b, d) size distribution as a function of particle diameter D (nm) in SALSA for typical polluted urban (a, b) and hazy rural conditions (c, d) (Zhang et al., 1999). Top legend: (number of size bins in subrange 1) + (number of size bins in subrange 2). The continuous log-normal size distribution is given by a solid black line. ΔV is the total volume concentration relative to the continuous log-normal size distribution.
3.1 Case description
The performance of the SALSA module in PALM is evaluated against measurements of the vertical variation of the aerosol number size distribution and concentrations in a street canyon (Pembroke Street) in central Cambridge, United Kingdom, over consecutive 24 h on 20–21 March 2007 (Kumar et al., 2008, 2009). During the measurement campaign, the predominant wind direction (WD) was from the northwest and perpendicular to the street canyon. Furthermore, there is a large pedestrian area upwind of the site with no traffic emissions, and hence emissions from adjacent streets were unlikely to affect the measurements. The building height is around 14–18 m on the upwind and 11–15 m on the downwind side of the street canyon (Fig. 3).
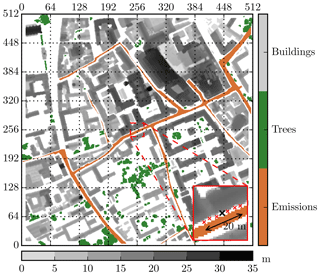
Figure 3Visualization of the simulation domain. The building height (m) is shown in grey shades, and the location of trees and emissions are in green and copper, respectively. The evaluation domain is marked with a red square. In the zoomed figure, the black cross indicates the measurement location and the red crosses the additional points at which the model output is evaluated against measurements. The grid represents the horizontal model grid. Data sources: elevation maps – Environment Agency (UK) data archive; land use footprints – Ordnance Survey 2014.
Aerosol size distributions in the size range D=5–2738 nm were measured pseudo-simultaneously at four heights (z=1.00, 2.25, 4.62, and 7.37 m above ground level, a.g.l.) using a fast-response differential mobility spectrometer (DMS500). The measurement location was on the northwestern side of Pembroke Street around 66 m from the closest intersection in the southwest. Traffic volumes along the street were simultaneously measured. Moreover, 30 min averaged meteorological data, including wind speed (U) and direction, ambient air temperature (T), and relative humidity (RH), were measured 40 m a.g.l. at some 500 m from the sampling site. For more information on the measurements, refer to Kumar et al. (2008).
The evaluation is done for three different periods (LT is for local time): 08:30–09:30 LT (morning), 21:00–22:00 LT (evening), and 03:00–04:00 LT (night-time). No daytime evaluation is presented here in order to minimize the role of thermal and vehicle-induced turbulence (VIT) on pollutant transport. The evening and night-time periods represent time after sunset, while the morning measurements were conducted under partly cloudy conditions.
3.2 Model domain and morphological data
Simulations are conducted over a domain of a grid box with the measurement site approximately at the centre of the domain (Fig. 3). A uniform grid spacing of m is applied within the lowest 96 m, and above the vertical grid Δz is stretched by a factor of 1.04, resulting in a total domain height of around 164 m and a maximum m.
The building-height and vegetation maps for the study area were constructed from 1 m horizontal resolution digital surface models (DSMs) and digital terrain models (DTMs) (Environment Agency UK data archive) following Kent et al. (2018). First, the DTM was subtracted from the DSM to set the terrain height to zero. Next, buildings were separated from other surface elements using a building footprint dataset from the OS MasterMap® Topography Layer (Ordnance Survey 2014). The vegetation map was formed from the remaining pixels by first removing the residue pixels around buildings and then performing dilation of the raster map to remove holes and unify vegetated areas. Only vegetation elements higher than m were included in the simulations. They were modelled as springtime deciduous broadleaf trees with a constant LAD =0.6 m2 m−3 from zv, min to the tree top. This LAD value was estimated as a lower limit for urban street trees in northern Europe in spring (Gillner et al., 2015). Excluding the details of local vegetation is acceptable since there are no trees close to the measurement site and overall the amount of vegetation is low.
Only road traffic lanes are defined as source areas for aerosol particles and gaseous compounds. The emission map (Fig. 3) was created by first extracting the roads, tracks, and paths from the OS MasterMap® Topography Layer and then manually removing pedestrian areas and small streets. Finally, raster erosion was applied to the remaining map to result in a lane width of 6–7 m on Pembroke Street.
3.3 Pollutant boundary conditions: emissions and background concentrations
In the simulations, a total aerosol number emission factor EF km−1 vehicle−1 is used (Table 3), which is an estimate specific to the measurement site (Kumar et al., 2009). EFn was distributed to a representative aerosol number size distribution with the shape estimated from the measured size distribution at the lowest level z=1.0 m during each simulation time (see Sect. S3). Aerosol emissions are assumed to be composed of mainly black (48 %) and organic carbon (48 %) and some H2SO4 (4 % of the total mass) (Maricq, 2007; Dallmann et al., 2014). Emission factors of gaseous compounds are instead calculated using the fleet-weighted road transport emission factors for 2008 by the National Atmospheric Emissions Inventory (NAEI; Walker, 2011) and the following fleet composition: 75 % petrol and 19 % diesel passenger cars, 1 % buses, 3 % light and 1 % heavy-duty diesel vehicles, and 1 % motorcycles. Since no EF or EFSVOC is given by NAEI, the following estimates were applied: EF (Arnold et al., 2006, 2012; Miyakawa et al., 2007) and EFSVOC=0.01EFNMOG (Zhao et al., 2017), where NMOG stands for non-methane organic gases. The latter is rather conservative compared to emission rates applied by Albriet et al. (2010) for a light-duty diesel truck. Both aerosol and gaseous emissions are introduced as constant fluxes per unit area.
Table 3Emission factors (EFs) applied in the simulations for all gaseous compounds and aerosol number n.

The background aerosol particle number and trace gas concentrations are produced with the trajectory model for Aerosol Dynamics, gas and particle phase CHEMistry and radiative transfer (ADCHEM; Roldin et al., 2011). Similar to Öström et al. (2017), ADCHEM was operated as a one-dimensional column trajectory model along HYSPLIT (Stein et al., 2015) air mass trajectories. In total, the gas and aerosol particle compositions were simulated along 48 trajectories arriving at central Cambridge between 20 March at 00:00 and 21 March at 23:00 (one every hour). All air mass trajectories started 5 days upwind of Cambridge over the Arctic Ocean (see Fig. S5). The anthropogenic trace gas emissions along the trajectories were taken from the European Monitoring and Evaluation Programme (EMEP) emission inventory for 2007 and the size-resolved primary particle emissions from the global emission inventory from Paasonen et al. (2016). These vertical profiles of the background concentrations (Sect. S5) are introduced to the simulation domain by a decycling method, in which constant background concentrations are fixed at the lateral boundaries.
3.4 Flow boundary conditions
In all simulations, a neutral atmospheric stratification is assumed for simplicity as no information on the atmospheric stratification or boundary layer height was available. Thus, a constant θ=T (z=40 m) (Table 4) is applied throughout the domain. The flow is driven by an external pressure gradient force above z=120 m. The gradient was set so that the horizontal mean U (z=40 m) over the whole simulation domain equals (±0.1 m s−1) the measured U (Table 4; see Fig. S7 for vertical profiles). Furthermore, the domain height was 164 m for all simulations. This is >13 h, where h=12.08 m is the mean building height over the domain, which should be enough to correctly resolve the small-scale turbulent structures within the urban canopy (Coceal et al., 2006).
Table 4Prevailing wind speed U, air temperature T, and relative humidity RH at z=40 m a.g.l., with the applied external pressure gradient force and traffic rates for each simulation hour. Wind direction is always from the northwest (WD ).

Cyclic lateral boundary conditions are applied for the flow, q, and e, which is reasonable since the surroundings do not notably differ from the simulation domain. A Neumann (free-slip) boundary condition is applied at the top boundary and also at the bottom and top for all scalars. The roughness height is z0=0.05 m (Letzel et al., 2012) and the drag coefficient applied for the trees is CD=0.5 (see Kent et al., 2017, and references within).
3.5 Simulations
Baseline simulations used to evaluate the performance of the model in the morning, evening, and at night are conducted with the default number of aerosol size bins (see Sect. 2.5). All aerosol processes, except nucleation, are switched on, and the following chemical components are included: H2SO4, OC, BC, HNO3, and NH3. All aerosol particle are assumed to be internally mixed and hygroscopic, and thereby no subrange 2b was applied.
In addition to the base run, the sensitivity to different aerosol processes and the number of size bins XB was examined for the morning simulation. Firstly, the following four simulations with are conducted: no aerosol processes (NOAP), only coagulation (COAG), only dry deposition (scheme Z01) on solid surfaces and vegetation (DEPO), and only condensation (COND). In the first three, particles are assumed to constitute only OC in order to limit computational costs, given that coagulation and dry deposition do not depend on aerosol composition. COND is instead performed with an identical set-up to the baseline simulation, except that other processes were switched off. Secondly, the sensitivity to XB is tested by replicating the baseline morning simulation with less (LB) and more bins (MB).
The advection of both momentum variables and scalars was based on the fifth-order advection scheme by Wicker and Skamarock (2002) together with a third-order Runge–Kutta time-stepping scheme (Williamson, 1980). The pressure term in the prognostic equations for momentum was calculated using the iterative multigrid scheme (Hackbusch, 1985). In order to enable similar flow conditions for all simulations, feedback to PALM was switched off; i.e. changes in specific humidity due to the condensation of water on aerosol particles were not allowed. Therefore q also remained constant. Here, ΔtSALSA=1.0 s in all simulations, which is a safe choice since the turbulence timescale is smaller than any aerosol process timescale (Kumar et al., 2008).
Simulations were conducted with the PALM model revision 3125. This was a model version prior to the 6.0 release, but reproducibility with version 6.0 was ensured by repeating the NOAP simulation. All simulations were first run for 2 h to create a quasi-stationary state of the flow, after which SALSA was switched on and run for 70 min. Data output was collected within the last 60 min with a 0.5–1 Hz frequency. Simulations were performed on the Centre for Scientific Computing (CSC) Taito supercluster. Using 64×64 Intel Haswell processor cores, one 70 min long simulation with SALSA required between 17 h (NOAP) and 52 h (MB) of computing time.
Modelled aerosol number concentrations were compared against measurements at the measurement location and six additional horizontal points on the northern side of the street canyon within the evaluation domain of 30 m×30 m (Fig. 3). The additional six profiles were analysed to include possible error in defining the measurement location and also to illustrate the variation in concentrations at different adjacent points in a street canyon. In the evaluation, the modelled values were linearly interpolated to the measurement heights and the measured size distributions to the modelled size bins. All modelled and measured values are hourly averaged.
4.1 Baseline simulations
To give a general picture of aerosol particle concentrations and dispersion in this study, Fig. 4 illustrates the modelled total aerosol number concentrations Ntot and wind speed U at z=3.5 m a.g.l. for all baseline simulations. The horizontal distribution of Ntot is shown to follow that of emissions (see Fig. 3) and, for instance, courtyards remain relatively clean. Nevertheless, wind controls the dispersion, which is seen as up to 70 % higher Ntot inside the street canyons for the calmer night-time compared to the more windy evening simulation (see Fig. S8) despite the lower emission rates at night. Interestingly, pollutant accumulation occurs close to the measurement site within the evaluation domain.
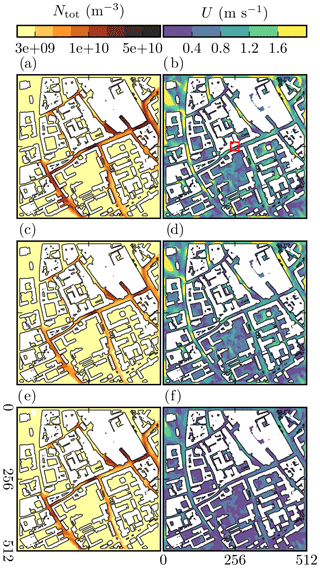
Figure 4Total aerosol number concentration Ntot (m−3, a, c, e) and wind speed U (m s−1, b, d, f) at z=3.5 m for the morning (a, b), evening (c, d), and night-time simulation (e, f) over the whole simulation domain of 512 m × 512 m. The evaluation domain (see Fig. 3) is marked with a red square in (b).
The modelled mean vertical profiles of Ntot compare well against the measured values (Fig. 5), especially in the morning. Indeed, the additional six profiles are also generally within a factor of 2of observations (see Fig. S9). The rate of change in Ntot in the vertical is correctly modelled except for a measured increase in concentrations within the lowest 2 m. Despite the modelled Ntot being 50 %–100 % higher than measured in the evening (Fig. 5b), concentrations are of the same order of magnitude. This deviation from measurements is comparable to typical differences in measured aerosol number concentrations with different instruments (Ankilov et al., 2002; Hornsby and Pryor, 2014). Comparing the mean values of all seven modelled profiles, their variation is shown to be larger than that between the measured and modelled Ntot at the exact measurement location.
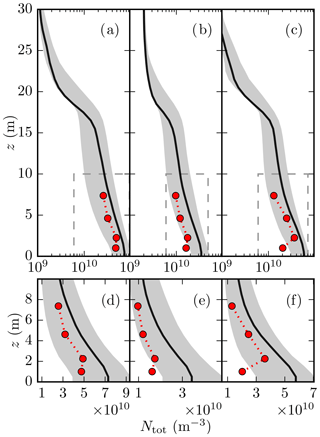
Figure 5Measured (red circles with a dotted line) and modelled (black solid line and grey shaded area) vertical profiles of total aerosol number concentration Ntot (m−3) for the morning (a, d), evening (b, e), and night-time (c, f) simulation. (d, e, f) Ntot in the lowest 10 m (area marked with a black dotted line in a, b, c) using a linear scale on the x axis. The black solid line shows the mean vertical profile at the measurement location and the grey shaded area the range of mean vertical profiles at six additional evaluation points within the evaluation domain.
Naturally, the coarse sectional representation of the aerosol size distribution with XB=10 means some details, such as a drop in concentrations at D≈60 nm (Fig. 6), cannot always be captured by the model. Furthermore, omitting any emission sources can produce error. For instance, an underestimation of the number of particles larger than 20 nm at z=2.25 m and z=4.62 m in the night-time (Fig. 6b and c) could stem from excluding some elevated sources, such as tailpipe emissions of trucks. Nonetheless, the model predictions are mainly within a factor of 2 of the measurements (see Fig. S10). The size distributions display very similar shapes to that of emissions, showing that the result is very sensitive to the quality of the input emission data.
At the same time, a mismatch with the measurements near the surface is to be expected, as the LES technique lacks reliability close to walls. Maronga et al. (2015), for instance, showed that the turbulent flow over a homogeneous surface is not well-resolved for the lowest six grid points, which corresponds to the lowest 5 m in these simulations. In that context, the modelled concentration fields agree exceptionally well with the measurements.
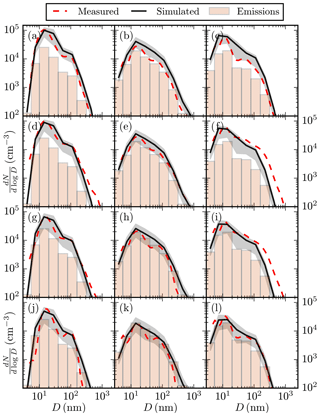
Figure 6Measured (red dashed line) and simulated (black) aerosol number size distribution dN∕dlog D (cm−3) as a function of particle diameter D (nm) in the morning (first column: a, d, g, j), evening (second column: b, e, h, k), and at night (third column: c, f, i, l) at levels z=1.00, 2.25, 4.62, and 7.37 m (top to bottom). The shape of the number size distribution for the emissions is given with bars (not in units cm−3). The black solid line shows the mean value at the measurement location and the grey shaded area the range of mean values at six additional evaluation points within the evaluation domain.
4.2 Sensitivity tests
4.2.1 Role of different aerosol processes
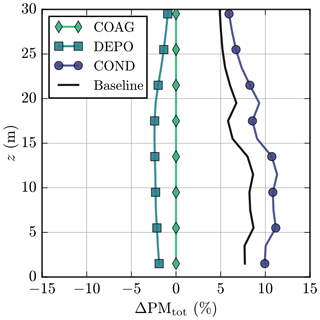
At the temporal and spatial scales applied in the simulations, dry deposition changes the total aerosol number concentrations most, with a relative difference ΔNtot< −20 %, especially in areas with vegetation but also in the wake of buildings (Fig. 7). Coagulation (COAG) changes Ntot only by less than 1 %. The impact of condensation and dissolutional growth (COND) on Ntot is negligible, as expected, since condensation only grows particles (Kumar et al., 2011).
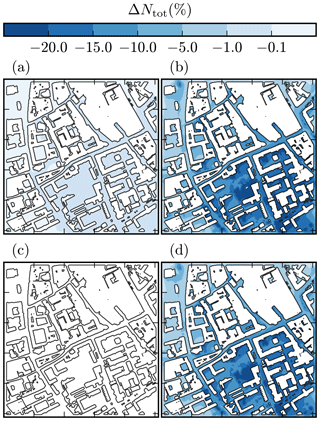
Figure 7Relative difference in the total aerosol number concentration ΔNtot (%) at z=3.5 m compared to NOAP for the (a) COAG, (b) DEPO, (c) COND, and (d) baseline simulation in the morning.
Neglecting all aerosol processes overestimates Ntot (see Fig. S11), and therefore including dry deposition is essential for modelling realistic Ntot. Above the roof level (z≳15 m), the role of dry deposition starts to weaken (Fig. 8), which is also attributable to lower aerosol concentrations. The smallest aerosol particles are most strongly affected by aerosol processes independently of modelling height (Fig. 9): this is because more efficient Brownian diffusion leads to higher deposition velocities vd (see Fig. 1) and coagulation rates. Furthermore, the smallest particles grow through condensation and dissolutional growth, which instead leads to less efficient removal by dry deposition. The impact of dry deposition and, to a lesser extent, coagulation decreases with height, and above the roof level the observed ΔNtot is likely due to aerosol processes acting upwind of the measurement site.
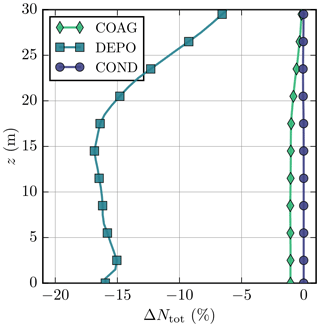
Figure 8Relative difference in the vertical profile of the total aerosol number concentration ΔNtot (%) compared to NOAP simulation for COAG (diamonds), DEPO (squares), and COND (circles) simulations in the morning. The difference is averaged over all seven evaluation points.
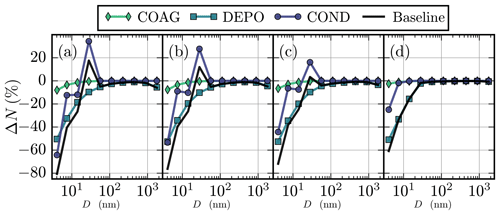
Figure 9Relative difference in the aerosol number concentration ΔN (%) compared to NOAP as a function of aerosol particle diameter D (nm) at levels (a) z=3.5 m, (b) z=10.5 m, (c) z=20.5 m, and (d) z=40.5 m in the morning. The difference is averaged over all seven evaluation points.
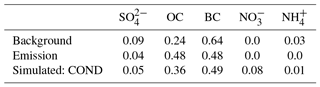
While condensation and dissolutional growth do not directly affect the number concentrations, the total mass and chemical composition of aerosol particles are shown to change. Over the whole evaluation domain, condensation and dissolutional growth increase PMtot by over 10 % below the roof height (Fig. 10). Comparing the initial chemical composition of the background aerosol concentrations and emissions (Table 5) with the modelled composition shows that the mass fraction of nitrates has especially increased, from 0 % to 8 %. This increased particulate mass of nitrates originates solely from the condensation of background gaseous HNO3 as there are no traffic-related emissions of gaseous HNO3. The simulated mass fraction of BC is very close to that of the aerosol emissions, while other mass fractions that also change due to condensation and dissolutional growth vary more. Deposition decreases PMtot, but the relative change is clearly lower than for Ntot, as the smallest particles, which are most affected by dry deposition, represent only a tiny share of the total mass.
Table 5Mass fractions of different chemical compounds for the aerosol background, emissions, and simulated concentrations for the COND simulation. The values are averaged over the whole evaluation domain within z<30 m.
4.2.2 Number of size bins
Further decreasing the number of aerosol size bins XB is a tempting method in order to reduce the computational load. Indeed, the total CPU time is reduced by −24 % when (LB), while setting (MB) increases the CPU time by +18 % compared to the baseline simulation in the morning. However, as shown in Sect. 2.5 and Fig. S12, the capability to describe the details of aerosol size distribution drops rapidly when decreasing XB.
Despite the background Ntot and total aerosol number emissions EFn being equal for the baseline, LB, and MB simulations, modelled Ntot values are not equal (Fig. 11). The difference is entirely attributable to the dissimilar effectiveness of aerosol processes with a lower (LB) and higher (MB) level of detail in representing the aerosol size distribution. Interestingly, using fewer size bins (LB) has a very minor impact on the horizontal field of Ntot, while more bins (MB) result in %. This is still smaller than ΔNtot due to deposition.

Figure 11Relative difference in the total number concentration ΔNtot (%) at z=3.5 m compared to the baseline simulation for the (a) LB and (b) MB simulation in the morning.
Comparing the modelled particulate masses is not that straightforward and is thus not represented here. The background concentrations and emissions of particulate mass differ between the simulations because the mass size distribution is calculated from the sectional number size distribution, which is different for all simulations.
This article represents a novel, high-resolution, LES-based urban aerosol model that resolves aerosol particle concentrations, size distributions, and chemical compositions at spatial and temporal scales of 1.0 m and 1.0 s for entire neighbourhoods.
An evaluation study of the vertical variation of the aerosol number size distribution and total number concentration in a simple street canyon in central Cambridge, UK, shows good agreement against measurements. The model can predict the dilution of concentrations in the vertical as well as the number of aerosol particles in different size bins generally within a factor of 2 of observations. The spatial distribution of aerosol concentrations is mostly determined by the flow and emissions. As regards the individual impact of aerosol dynamic processes, dry deposition is shown to decrease local number concentrations by over 20 %, which is nonetheless at the lower end of % estimated by Huang et al. (2014) for an open space with traffic. Coagulation has a very minor impact, which agrees with previous timescale analyses (Kumar et al., 2009; Zhang et al., 2004) and CFD modelling studies (Albriet et al., 2010; Huang et al., 2014; Wang and Zhang, 2012). Condensation and dissolutional growth increase particulate mass by over 10 %. The role of aerosol dynamic processes is shown as important for both number and mass, especially in areas with low wind speeds, such as in courtyards and the shelter of trees. Furthermore, comparing six additional modelling profiles to the measured one shows the limited representativeness of point measurements and supports performing air quality modelling which also gives the spatial variability of concentrations.
With increasing modelling complexity, the number of potential sources of modelling uncertainty is augmented. One of the largest sources of uncertainty is related to the quality of the emission data. A major reason to evaluate the aerosol model against the dataset by Kumar et al. (2008) was that the measured concentrations were mainly affected by traffic emissions along Pembroke Street, which simplified the emission estimations.
Aerosol modelling uncertainties caused by simplifying assumptions and model design are discussed in detail in Kokkola et al. (2008). One of the main challenges in simulating both the aerosol number and mass also in this study is the limited number of aerosol size bins, whereas the aerosol dynamic processes have less impact. Another inevitable error in sectional aerosol modelling is made when assuming a spherical particle shape and defining the aerosol volume from the bin mean diameter. Despite these limitations, the model simulated the observed number concentrations correctly.
Further arguments for applying the selected dataset were the availability of measurements of the vertical variability of aerosol number size distribution at high temporal resolution, but also the simplicity of the urban morphology at the measurement location. The influence of aerosol dynamic processes on aerosol concentration is determined by their size distribution, and thus measurements only of the total number concentration or particulate mass (e.g. Weber et al., 2006) were considered insufficient for this model evaluation. To our knowledge, there are only a few datasets on the vertical variation of the aerosol size distribution in an urban environment (Kumar et al., 2008; Li et al., 2007; Marini et al., 2015; Quang et al., 2012; Sajani et al., 2018). Of these datasets, the measurement location of Kumar et al. (2008) in a street canyon with no urban vegetation was simple enough for the first evaluation study. Modelling individual street trees and their aerodynamic impact without exact information on the distribution of leaf area introduces another source of uncertainty for resolving the flow. Furthermore, dry deposition is strongly tree species dependent (e.g. Popek et al., 2013; Sæbø et al., 2012) and therefore sensitive to the correct modelling of different species. Finally, high-resolution topography and land use information were freely available for this specific site.
At the same time, no high-resolution evaluation data for the flow were available, and therefore the modelling set-up was kept as simple as possible. Hence, the thermal and vehicle-induced turbulence was excluded from the simulations. The increase in Ntot for z=1.0–2.25 m observed in the measurements could be explained by either of the two sources of turbulence. Kumar et al. (2008) argued that the increase is likely due to more efficient dry deposition near the surface or the complex dispersion pattern within the canyon caused by both topography and vehicle-induced turbulence.
Keeping in mind the aforementioned uncertainties and required computational resources, the presented model provides a novel and flexible tool to study, for example, how the shape, size, and location of urban obstacles affect air pollutant transport and transformation at a neighbourhood scale. For instance, the potential of urban vegetation to improve air quality by acting as a biological aerosol filter (Beckett et al., 1998) depends on the size-dependent deposition velocity of aerosol particles, which is explicitly calculated within the model. The model can also provide information at high enough resolution to perform air pollutant exposure studies or to design a representative air pollution monitoring network. The aerosol module SALSA can be further coupled with an online chemistry module, which are both embedded in the PALM model system as so-called PALM-4U components. This will extend the applicability of the model from aerosol processes to more complex chemical processes and will allow researchers to examine different urban processes simultaneously such as radiation or thermal comfort. Moreover, ongoing model development aims at extending the application of the model from supercomputing environments to personal PCs in future (Maronga et al., 2019).
The PALM code, including the sectional aerosol model SALSA, can be freely downloaded from http://palm.muk.uni-hannover.de (last access: 29 March 2019). The distribution is under the GNU General Public License v3. More about the code management, versioning, and revision control of PALM can be found in Maronga et al. (2015). The exact version of the source code used in this study is additionally freely available at https://doi.org/10.5281/zenodo.2575325. The stand-alone version of the SALSA model is freely available at https://github.com/UCLALES-SALSA/SALSA-standalone/ (last access: 29 March 2019) and the input datasets at https://doi.org/10.5281/zenodo.1565752 (Kurppa, 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-12-1403-2019-supplement.
MK developed the model code with support from HK, JT, and BM. MK and CK prepared the morphological data and PK the evaluation data. MK, AH, MA, and LJ designed the simulations and MK carried them out. MK prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
MK acknowledges Sasu Karttunen for technical support and Basit Khan, Farah Kanani-Sühring, Renate Forkel, and Sabine Banzhaf for cooperation, valuable discussions, and model testing. This study was financially supported by the doctoral programme in Atmospheric Sciences (ATM-DP, University of Helsinki), the Helsinki Metropolitan Region Urban Research Program and the Academy of Finland (181255, 277664), the trans-national project SMURBS (http://www.smurbs.eu/, last access: 29 March 2019; grant agreement no. 689443), and the Helsinki metropolitan Air Quality Testbed (HAQT).
This paper was edited by Samuel Remy and reviewed by Bo Yang and one anonymous referee.
Ackermann, I. J., Hass, H., Memmesheimer, M., Ebel, A., Binkowski, F. S., and Shankar, U.: Modal aerosol dynamics model for Europe: development and first applications, Atmos. Environ., 32, 2981–2999, https://doi.org/10.1016/S1352-2310(98)00006-5, 1998. a
Albriet, B., Sartelet, K., Lacour, S., Carissimo, B., and Seigneur, C.: Modelling aerosol number distributions from a vehicle exhaust with an aerosol CFD model, Atmos. Environ., 44, 1126–1137, https://doi.org/10.1016/j.atmosenv.2009.11.025, 2010. a, b, c
Ankilov, A., Baklanov, A., Colhoun, M., Enderle, K.-H., Gras, J., Julanov, Y., Kaller, D., Lindner, A., Lushnikov, A., Mavliev, R., McGovern, F., Mirme, A., O'Connor, T., Podzimek, J., Preining, O., Reischl, G., Rudolf, R., Sem, G., Szymanski, W., Tamm, E., Vrtala, A., Wagner, P., Winklmayr, W., and Zagaynov, V.: Intercomparison of number concentration measurements by various aerosol particle counters, Atmos. Res., 62, 177–207, https://doi.org/10.1016/S0169-8095(02)00010-8, 2002. a
Antoniou, N., Montazeri, H., Wigo, H., Neophytou, M. K.-A., Blocken, B., and Sandberg, M.: CFD and wind-tunnel analysis of outdoor ventilation in a real compact heterogeneous urban area: Evaluation using “air delay”, Build. Environ., 126, 355–372, https://doi.org/10.1016/j.buildenv.2017.10.013, 2017. a
Anttila, T., Kerminen, V.-M., and Lehtinen, K. E.: Parameterizing the formation rate of new particles: The effect of nuclei self-coagulation, J. Aerosol Sci., 41, 621–636, https://doi.org/10.1016/j.jaerosci.2010.04.008, 2010. a
Arakawa, A. and Lamb, V. R.: Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model, in: General Circulation Models of the Atmosphere, in: Methods in Computational Physics: Advances in Research and Applications, edited by: Chang, J., Elsevier, 17, 173–265, https://doi.org/10.1016/B978-0-12-460817-7.50009-4, 1977. a
Arnold, F., Pirjola, L., Aufmhoff, H., Schuck, T., Lähde, T., and Hämeri, K.: First gaseous sulfuric acid measurements in automobile exhaust: Implications for volatile nanoparticle formation, Atmos. Environ., 40, 7097–7105, https://doi.org/10.1016/j.atmosenv.2006.06.038, 2006. a
Arnold, F., Pirjola, L., Rönkkö, T., Reichl, U., Schlager, H., Lähde, T., Heikkilä, J., and Keskinen, J.: First Online Measurements of Sulfuric Acid Gas in Modern Heavy-Duty Diesel Engine Exhaust: Implications for Nanoparticle Formation, Environ. Sci. Technol., 46, 11227–11234, https://doi.org/10.1021/es302432s, 2012. a
Auvinen, M., Järvi, L., Hellsten, A., Rannik, Ü., and Vesala, T.: Numerical framework for the computation of urban flux footprints employing large-eddy simulation and Lagrangian stochastic modeling, Geosci. Model Dev., 10, 4187–4205, https://doi.org/10.5194/gmd-10-4187-2017, 2017. a
Beard, K. V. and Ochs, H. T.: Collection and coalescence efficiencies for accretion, J. Geophys. Res., 89, 7165–7169, https://doi.org/10.1029/JD089iD05p07165, 1984. a
Beckett, K., Freer-Smith, P., and Taylor, G.: Urban woodlands: their role in reducing the effects of particulate pollution, Environ. Pollut., 99, 347–360, https://doi.org/10.1016/S0269-7491(98)00016-5, 1998. a
Chen, J.-P. and Lamb, D.: Simulation of Cloud Microphysical and Chemical Processes Using a Multicomponent Framework. Part I: Description of the Microphysical Model, J. Aerosol Sci., 51, 2613–2630, https://doi.org/10.1175/1520-0469(1994)051<2613:SOCMAC>2.0.CO;2, 1994. a
Coceal, O., Thomas, T. G., Castro, I. P., and Belcher, S. E.: Mean Flow and Turbulence Statistics Over Groups of Urban-like Cubical Obstacles, Bound.-Lay. Meteorol., 121, 491–519, https://doi.org/10.1007/s10546-006-9076-2, 2006. a
Dallmann, T. R., Onasch, T. B., Kirchstetter, T. W., Worton, D. R., Fortner, E. C., Herndon, S. C., Wood, E. C., Franklin, J. P., Worsnop, D. R., Goldstein, A. H., and Harley, R. A.: Characterization of particulate matter emissions from on-road gasoline and diesel vehicles using a soot particle aerosol mass spectrometer, Atmos. Chem. Phys., 14, 7585–7599, https://doi.org/10.5194/acp-14-7585-2014, 2014. a
Deardorff, J. W.: Stratocumulus-capped mixed layers derived from a three-dimensional model, Bound.-Lay. Meteorol., 18, 495–527, https://doi.org/10.1007/BF00119502, 1980. a
Fuchs, N.: The Mechanics of Aerosols, translated from the Russian by: Daisley, R. E. and Fuchs, M., New York, Pergamon Press, 1964. a
Gakidou, E., Afshin, A., Abajobir, et al.: Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks, 1990–2016: a systematic analysis for the Global Burden of Disease Study 2016, The Lancet, 390, 1345–1422, https://doi.org/10.1016/S0140-6736(17)32366-8, 2017. a
García-Sánchez, C., van Beeck, J., and Gorlé, C.: Predictive large eddy simulations for urban flows: Challenges and opportunities, Build. Environ., 139, 146–156, https://doi.org/10.1016/j.buildenv.2018.05.007, 2018. a
Giles-Corti, B., Vernez-Moudon, A., Reis, R., Turrell, G., Dannenberg, A. L., Badland, H., Foster, S., Lowe, M., Sallis, J. F., Stevenson, M., and Owen, N.: City planning and population health: a global challenge, The Lancet, 388, 2912–2924, 2016. a
Gillner, S., Vogt, J., Tharang, A., Dettmann, S., and Roloff, A.: Role of street trees in mitigating effects of heat and drought at highly sealed urban sites, Landscape Urban Plan., 143, 33–42, https://doi.org/10.1016/j.landurbplan.2015.06.005, 2015. a
Gong, S. L., Barrie, L. A., Blanchet, J.-P., von Salzen, K., Lohmann, U., Lesins, G., Spacek, L., Zhang, L. M., Girard, E., Lin, H., Leaitch, R., Leighton, H., Chylek, P., and Huang, P.: Canadian Aerosol Module: A size-segregated simulation of atmospheric aerosol processes for climate and air quality models 1. Module development, J. Geophys. Res., 108, 4007, https://doi.org/10.1029/2001JD002002, 2003. a
Hackbusch, W.: Multi-grid methods and applications, 1st edn., Springer-Verlag, Berlin Heidelberg, 1985. a
Harlow, F. H. and Welch, J. E.: Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface, Phys. Fluids, 8, 2182–2189, https://doi.org/10.1063/1.1761178, 1965. a
Hornsby, K. E. and Pryor, S. C.: A Laboratory Comparison of Real-Time Measurement Methods for 10–100-nm Particle Size Distributions, Aerosol Sci. Tech., 48, 571–582, https://doi.org/10.1080/02786826.2014.901488, 2014. a
Huang, L., Gong, S. L., Gordon, M., Liggio, J., Staebler, R., Stroud, C. A., Lu, G., Mihele, C., Brook, J. R., and Jia, C. Q.: Aerosol–computational fluid dynamics modeling of ultrafine and black carbon particle emission, dilution, and growth near roadways, Atmos. Chem. Phys., 14, 12631–12648, https://doi.org/10.5194/acp-14-12631-2014, 2014. a, b, c, d
Jacobson, M. Z.: Fundamentals of Atmospheric Modeling, 2nd edn., Cambridge University Press, New York, 2005. a, b, c
Kanda, M., Inagaki, A., Miyamoto, T., Gryschka, M., and Raasch, S.: A New Aerodynamic Parametrization for Real Urban Surfaces, Bound.-Lay. Meteorol., 148, 357–377, https://doi.org/10.1007/s10546-013-9818-x, 2013. a
Kelly, F. J. and Fussell, J. C.: Size, source and chemical composition as determinants of toxicity attributable to ambient particulate matter, Atmos. Environ., 60, 504–526, https://doi.org/10.1016/j.atmosenv.2012.06.039, 2012. a
Kent, C. W., Grimmond, S., and Gatey, D.: Aerodynamic roughness parameters in cities: Inclusion of vegetation, J. Wind Eng. Ind. Aerod., 169, 168–176, https://doi.org/10.1016/j.jweia.2017.07.016, 2017. a
Kent, C. W., Lee, K., Ward, H. C., Hong, J.-W., Hong, J., Gatey, D., and Grimmond, S.: Aerodynamic roughness variation with vegetation: analysis in a suburban neighbourhood and a city park, Urban Ecosyst., 21, 227–243, https://doi.org/10.1007/s11252-017-0710-1, 2018. a
Kerminen, V.-M. and Kulmala, M.: Analytical formulae connecting the “real” and the “apparent” nucleation rate and the nuclei number concentration for atmospheric nucleation events, J. Aerosol Sci., 33, 609–622, https://doi.org/10.1016/S0021-8502(01)00194-X, 2002. a
Kokkola, H., Korhonen, H., Lehtinen, K. E. J., Makkonen, R., Asmi, A., Järvenoja, S., Anttila, T., Partanen, A.-I., Kulmala, M., Järvinen, H., Laaksonen, A., and Kerminen, V.-M.: SALSA – a Sectional Aerosol module for Large Scale Applications, Atmos. Chem. Phys., 8, 2469–2483, https://doi.org/10.5194/acp-8-2469-2008, 2008. a, b, c
Kokkola, H., Kühn, T., Laakso, A., Bergman, T., Lehtinen, K. E. J., Mielonen, T., Arola, A., Stadtler, S., Korhonen, H., Ferrachat, S., Lohmann, U., Neubauer, D., Tegen, I., Siegenthaler-Le Drian, C., Schultz, M. G., Bey, I., Stier, P., Daskalakis, N., Heald, C. L., and Romakkaniemi, S.: SALSA2.0: The sectional aerosol module of the aerosol–chemistry–climate model ECHAM6.3.0-HAM2.3-MOZ1.0, Geosci. Model Dev., 11, 3833–3863, https://doi.org/10.5194/gmd-11-3833-2018, 2018. a, b
Kudzotsa, I., Kokkola, H., Tonttila, J., Raatikainen, T., and Romakkaniemi, S.: Implementing Gas-to-Particle Partitioning of Semi-Volatile Inorganic Compounds in UCLALES-SALSA V1.6, Geosci. Model Dev., in preparation, 2019. a
Kumar, P., Fennell, P., Langley, D., and Britter, R.: Pseudo-simultaneous measurements for the vertical variation of coarse, fine and ultrafine particles in an urban street canyon, Atmos. Environ., 42, 4304–4319, https://doi.org/10.1016/j.atmosenv.2008.01.010, 2008. a, b, c, d, e, f, g, h
Kumar, P., Garmory, A., Ketzel, M., Berkowicz, R., and Britter, R.: Comparative study of measured and modelled number concentrations of nanoparticles in an urban street canyon, Atmos. Environ., 43, 949–958, https://doi.org/10.1016/j.atmosenv.2008.10.025, 2009. a, b, c
Kumar, P., Ketzel, M., Vardoulakis, S., Pirjola, L., and Britter, R.: Dynamics and dispersion modelling of nanoparticles from road traffic in the urban atmospheric environment – a review, J. Aerosol Sci., 42, 580–603, 2011. a, b
Kurppa, M.: Input data for performing a model evaluation of the sectional aerosol module SALSA embedded to PALM model system 6.0, version 1.0.1, Zenodo, https://doi.org/10.5281/zenodo.1565752, 2018. a
Kurppa, M., Hellsten, A., Auvinen, M., Raasch, S., Vesala, T., and Järvi, L.: Ventilation and Air Quality in City Blocks Using Large-Eddy Simulation–Urban Planning Perspective, Atmosphere, 9, 65, https://doi.org/10.3390/atmos9020065, 2018. a
Lehtinen, K. E., Maso, M. D., Kulmala, M., and Kerminen, V.-M.: Estimating nucleation rates from apparent particle formation rates and vice versa: Revised formulation of the Kerminen–Kulmala equation, J. Aerosol Sci., 38, 988–994, https://doi.org/10.1016/j.jaerosci.2007.06.009, 2007. a
Letzel, M. O., Krane, M., and Raasch, S.: High resolution urban large-eddy simulation studies from street canyon to neighbourhood scale, Atmos. Environ., 42, 8770–8784, https://doi.org/10.1016/j.atmosenv.2008.08.001, 2008. a
Letzel, M. O., Helmke, C., Ng, E., An, X., Lai, A., and Raasch, S.: LES case study on pedestrian level ventilation in two neighbourhoods in Hong Kong, Meteorol. Z., 21, 575–589, https://doi.org/10.1127/0941-2948/2012/0356, 2012. a
Li, X., Wang, J., Tu, X., Liu, W., and Huang, Z.: Vertical variations of particle number concentration and size distribution in a street canyon in Shanghai, China, Sci. Total Environ., 378, 306–316, https://doi.org/10.1016/j.scitotenv.2007.02.040, 2007. a
Liu, X., Easter, R. C., Ghan, S. J., Zaveri, R., Rasch, P., Shi, X., Lamarque, J.-F., Gettelman, A., Morrison, H., Vitt, F., Conley, A., Park, S., Neale, R., Hannay, C., Ekman, A. M. L., Hess, P., Mahowald, N., Collins, W., Iacono, M. J., Bretherton, C. S., Flanner, M. G., and Mitchell, D.: Toward a minimal representation of aerosols in climate models: description and evaluation in the Community Atmosphere Model CAM5, Geosci. Model Dev., 5, 709–739, https://doi.org/10.5194/gmd-5-709-2012, 2012. a
Liu, Y. H., He, Z., and Chan, T. L.: Three-Dimensional Simulation of Exhaust Particle Dispersion and Concentration Fields in the Near-Wake Region of the Studied Ground Vehicle, Aerosol Sci. Technol., 45, 1019–1030, https://doi.org/10.1080/02786826.2011.580021, 2011. a, b
Maricq, M. M.: Chemical characterization of particulate emissions from diesel engines: A review, J. Aerosol Sci., 38, 1079–1118, https://doi.org/10.1016/j.jaerosci.2007.08.001, 2007. a
Marini, S., Buonanno, G., Stabile, L., and Avino, P.: A benchmark for numerical scheme validation of airborne particle exposure in street canyons, Environ. Sci. Pollut. R., 22, 2051–2063, https://doi.org/10.1007/s11356-014-3491-6, 2015. a
Maronga, B. and Bosveld, F. C.: Key parameters for the life cycleof nocturnal radiation fog: a comprehensive large-eddy simulation study, Q. J. Roy. Meteor. Soc., 143, 2463–2480, https://doi.org/10.1002/qj.3100, 2017. a
Maronga, B., Gryschka, M., Heinze, R., Hoffmann, F., Kanani-Sühring, F., Keck, M., Ketelsen, K., Letzel, M. O., Sühring, M., and Raasch, S.: The Parallelized Large-Eddy Simulation Model (PALM) version 4.0 for atmospheric and oceanic flows: model formulation, recent developments, and future perspectives, Geosci. Model Dev., 8, 2515–2551, https://doi.org/10.5194/gmd-8-2515-2015, 2015. a, b, c, d
Maronga, B., Gross, G., Raasch, S., Banzhaf, S., Forkel, R., Heldens, W., Kanani-Sühring, F., Matzarakis, A., Mauder, M., Pavlik, D., Pfafferot, J., Seckmeyer, G., Sieker, H., and Trusilova, K.: Development of a new urban climate model based on the model PALM – Project overview, planned work, and first achievements, Meteorol. Z., https://doi.org/10.1127/metz/2019/0909, 2019. a, b
McGraw, R.: Description of Aerosol Dynamics by the Quadrature Method of Moments, Aerosol Sci. Tech., 27, 255–265, https://doi.org/10.1080/02786829708965471, 1997. a
Mingxuan, W., Xiaohong, L., Leiming, Z., Chenglai, W., Zheng, L., Po-Lun, M., Hailong, W., Simone, T., Natalie, M., Hitoshi, M., and C., E. R.: Impacts of Aerosol Dry Deposition on Black Carbon Spatial Distributions and Radiative Effects in the Community Atmosphere Model CAM5, J. Adv. Model. Earth Sy., 10, 1150–1171, https://doi.org/10.1029/2017MS001219, 2018. a
Miyakawa, T., Takegawa, N., and Kondo, Y.: Removal of sulfur dioxide and formation of sulfate aerosol in Tokyo, J. Geophys. Res., 112, D13209, https://doi.org/10.1029/2006JD007896, 2007. a
Moeng, C.-H. and Wyngaard, J. C.: Spectral Analysis of Large-Eddy Simulations of the Convective Boundary Layer, J. Atmos. Sci., 45, 3573–3587, https://doi.org/10.1175/1520-0469(1988)045<3573:SAOLES>2.0.CO;2, 1988. a
Monin, A. S. and Obukhov, A.: Basic laws of turbulent mixing in the surface layer of the atmosphere, Trudy Geofiz, Instituta Akademii Nauk, SSSR, 24, 163–187, 1954 (in Russian). a
Napari, I., Noppel, M., Vehkamäki, H., and Kulmala, M.: An improved model for ternary nucleation of sulfuric acid–ammonia–water, J. Chem. Phys., 116, 4221–4227, https://doi.org/10.1063/1.1450557, 2002a. a
Napari, I., Noppel, M., Vehkamäki, H., and Kulmala, M.: Parametrization of ternary nucleation rates for H2SO4-NH3-H2O vapors, J. Geophys. Res., 107, 4381, https://doi.org/10.1029/2002JD002132, 2002b. a
Öström, E., Putian, Z., Schurgers, G., Mishurov, M., Kivekäs, N., Lihavainen, H., Ehn, M., Rissanen, M. P., Kurtén, T., Boy, M., Swietlicki, E., and Roldin, P.: Modeling the role of highly oxidized multifunctional organic molecules for the growth of new particles over the boreal forest region, Atmos. Chem. Phys., 17, 8887–8901, https://doi.org/10.5194/acp-17-8887-2017, 2017. a
Paasonen, P., Kupiainen, K., Klimont, Z., Visschedijk, A., Denier van der Gon, H. A. C., and Amann, M.: Continental anthropogenic primary particle number emissions, Atmos. Chem. Phys., 16, 6823–6840, https://doi.org/10.5194/acp-16-6823-2016, 2016. a
Park, S.-B., Baik, J.-J., and Lee, S.-H.: Impacts of Mesoscale Wind on Turbulent Flow and Ventilation in a Densely Built-up Urban Area, J. Appl. Meteorol. Clim., 54, 811–824, https://doi.org/10.1175/JAMC-D-14-0044.1, 2015. a
Petroff, A. and Zhang, L.: Development and validation of a size-resolved particle dry deposition scheme for application in aerosol transport models, Geosci. Model Dev., 3, 753–769, https://doi.org/10.5194/gmd-3-753-2010, 2010. a, b, c, d
Popek, R., Gawrońska, H., Wrochna, M., Gawroński, S. W., and Sæbø, A.: Particulate Matter on Foliage of 13 Woody Species: Deposition on Surfaces and Phytostabilisation in Waxes – a 3-Year Study, Int. J. Phytoremediat., 15, 245–256, https://doi.org/10.1080/15226514.2012.694498, 2013. a
Prandtl, L.: Bericht uber Untersuchungen zur ausgebildeten Turbulenz, ZAMM-Z. Angew. Math. Me., 5, 136–139, 1925. a
Pryor, S. C. and Binkowski, F. S.: An Analysis of the Time Scales Associated with Aerosol Processes during Dry Deposition, Aerosol Sci. Tech., 38, 1091–1098, https://doi.org/10.1080/027868290885827, 2004. a
Quang, T. N., He, C., Morawska, L., Knibbs, L. D., and Falk, M.: Vertical particle concentration profiles around urban office buildings, Atmos. Chem. Phys., 12, 5017–5030, https://doi.org/10.5194/acp-12-5017-2012, 2012. a
Raasch, S. and Schröter, M.: PALM – A large-eddy simulation model performing on massively parallel computers, Meteorol. Z., 10, 363–372, 2001. a
Razak, A. A., Hagishima, A., Ikegaya, N., and Tanimoto, J.: Analysis of airflow over building arrays for assessment of urban wind environment, Build. Environ., 59, 56–65, https://doi.org/10.1016/j.buildenv.2012.08.007, 2013. a
Resler, J., Krč, P., Belda, M., Juruš, P., Benešová, N., Lopata, J., Vlček, O., Damašková, D., Eben, K., Derbek, P., Maronga, B., and Kanani-Sühring, F.: PALM-USM v1.0: A new urban surface model integrated into the PALM large-eddy simulation model, Geosci. Model Dev., 10, 3635–3659, https://doi.org/10.5194/gmd-10-3635-2017, 2017. a, b
Riipinen, I., Sihto, S.-L., Kulmala, M., Arnold, F., Dal Maso, M., Birmili, W., Saarnio, K., Teinilä, K., Kerminen, V.-M., Laaksonen, A., and Lehtinen, K. E. J.: Connections between atmospheric sulphuric acid and new particle formation during QUEST III–IV campaigns in Heidelberg and Hyytiälä, Atmos. Chem. Phys., 7, 1899–1914, https://doi.org/10.5194/acp-7-1899-2007, 2007. a, b
Roldin, P., Swietlicki, E., Schurgers, G., Arneth, A., Lehtinen, K. E. J., Boy, M., and Kulmala, M.: Development and evaluation of the aerosol dynamics and gas phase chemistry model ADCHEM, Atmos. Chem. Phys., 11, 5867–5896, https://doi.org/10.5194/acp-11-5867-2011, 2011. a
Rönkkö, T., Virtanen, A., Kannosto, J., Keskinen, J., Lappi, M., and Pirjola, L.: Nucleation Mode Particles with a Nonvolatile Core in the Exhaust of a Heavy Duty Diesel Vehicle, Environ. Sci. Technol., 41, 6384–6389, https://doi.org/10.1021/es0705339, 2007. a
Saiki, E. M., Moeng, C.-H., and Sullivan, P. P.: Large-Eddy Simulation Of The Stably Stratified Planetary Boundary Layer, Bound.-Lay. Meteorol., 95, 1–30, https://doi.org/10.1023/A:1002428223156, 2000. a
Sajani, S. Z., Marchesi, S., Trentini, A., Bacco, D., Zigola, C., Rovelli, S., Ricciardelli, I., Maccone, C., Lauriola, P., Cavallo, D. M., Poluzzi, V., Cattaneo, A., and Harrison, R. M.: Vertical variation of PM2.5 mass and chemical composition, particle size distribution, NO2, and BTEX at a high rise building, Environmental Pollution, 235, 339–349, https://doi.org/10.1016/j.envpol.2017.12.090, 2018. a
Sihto, S.-L., Kulmala, M., Kerminen, V.-M., Dal Maso, M., Petäjä, T., Riipinen, I., Korhonen, H., Arnold, F., Janson, R., Boy, M., Laaksonen, A., and Lehtinen, K. E. J.: Atmospheric sulphuric acid and aerosol formation: implications from atmospheric measurements for nucleation and early growth mechanisms, Atmos. Chem. Phys., 6, 4079–4091, https://doi.org/10.5194/acp-6-4079-2006, 2006. a
Steffens, J. T., Heist, D. K., Perry, S. G., and Zhang, K. M.: Modeling the effects of a solid barrier on pollutant dispersion under various atmospheric stability conditions, Atmos. Environ., 69, 76–85, https://doi.org/10.1016/j.atmosenv.2012.11.051, 2013. a
Stein, A. F., Draxler, R. R., Rolph, G. D., Stunder, B. J. B., Cohen, M. D., and Ngan, F.: NOAA's HYSPLIT Atmospheric Transport and Dispersion Modeling System, B. Am. Meteorol. Soc., 96, 2059–2077, https://doi.org/10.1175/BAMS-D-14-00110.1, 2015. a
Stokes, R. H. and Robinson, R. A.: Interactions in Aqueous Nonelectrolyte Solutions. I. Solute-Solvent Equilibria, J. Phys. Chem., 70, 2126–2131, https://doi.org/10.1021/j100879a010, 1966. a
Sæbø, A., Popek, R., Nawrot, B., Hanslin, H., Gawronska, H., and Gawronski, S.: Plant species differences in particulate matter accumulation on leaf surfaces, Sci. Total Environ., 427–428, 347–354, https://doi.org/10.1016/j.scitotenv.2012.03.084, 2012. a
Tominaga, Y. and Stathopoulos, T.: Ten questions concerning modeling of near-field pollutant dispersion in the built environment, Build. Environ., 105, 390–402, https://doi.org/10.1016/j.buildenv.2016.06.027, 2016. a
Tong, Z., Baldauf, R. W., Isakov, V., Deshmukh, P., and Zhang, K. M.: Roadside vegetation barrier designs to mitigate near-road air pollution impacts, Sci. Total Environ., 541, 920–927, https://doi.org/10.1016/j.scitotenv.2015.09.067, 2016a. a
Tong, Z., Chen, Y., Malkawi, A., Adamkiewicz, G., and Spengler, J. D.: Quantifying the impact of traffic-related air pollution on the indoor air quality of a naturally ventilated building, Environ. Int., 89–90, 138–146, https://doi.org/10.1016/j.envint.2016.01.016, 2016b. a
Tonttila, J., Maalick, Z., Raatikainen, T., Kokkola, H., Kühn, T., and Romakkaniemi, S.: UCLALES-SALSA v1.0: a large-eddy model with interactive sectional microphysics for aerosol, clouds and precipitation, Geosci. Model Dev., 10, 169–188, https://doi.org/10.5194/gmd-10-169-2017, 2017. a, b
Topping, D., Lowe, D., and McFiggans, G.: Partial Derivative Fitted Taylor Expansion: An efficient method for calculating gas-liquid equilibria in atmospheric aerosol particles: 1. Inorganic compounds, J. Geophys. Res., 114, D04304, https://doi.org/10.1029/2008JD010099, 2009. a
Uhrner, U., von Löwis, S., Vehkamäki, H., Wehner, B., Bräsel, S., Hermann, M., Stratmann, F., Kulmala, M., and Wiedensohler, A.: Dilution and aerosol dynamics within a diesel car exhaust plume–CFD simulations of on-road measurement conditions, Atmos. Environ., 41, 7440–7461, https://doi.org/10.1016/j.atmosenv.2007.05.057, 2007. a, b
Vehkamäki, H., Kulmala, M., Napari, I., Lehtinen, K. E. J., Timmreck, C., Noppel, M., and Laaksonen, A.: An improved parameterization for sulfuric acid–water nucleation rates for tropospheric and stratospheric conditions, J. Geophys. Res., 107, 4622, https://doi.org/10.1029/2002JD002184, 2002. a
Vignati, E., Wilson, J., and Stier, P.: M7: An efficient size-resolved aerosol microphysics module for large-scale aerosol transport models, J. Geophys. Res., 109, D22202, https://doi.org/10.1029/2003JD004485, 2004. a
Walker, H.: Fleet weighted Road Transport Emission Factor 2008, National Atmospheric Emissions Inventory, available at: http://naei.beis.gov.uk/data/ef-transport (last access: 25 September 2018), 2011. a
Wang, Y. J. and Zhang, K. M.: Coupled turbulence and aerosol dynamics modeling of vehicle exhaust plumes using the CTAG model, Atmos. Environ., 59, 284–293, https://doi.org/10.1016/j.atmosenv.2012.04.062, 2012. a, b
Weber, S., Kuttler, W., and Weber, K.: Flow characteristics and particle mass and number concentration variability within a busy urban street canyon, Atmos. Environ., 40, 7565–7578, https://doi.org/10.1016/j.atmosenv.2006.07.002, 2006. a
Whitby, E. R. and McMurry, P. H.: Modal Aerosol Dynamics Modeling, Aerosol Sci. Tech., 27, 673–688, https://doi.org/10.1080/02786829708965504, 1997. a
WHO: Ambient air pollution: A global assessment of exposure and burden of disease, World Health Organization (WHO), 131 pp., 2016. a
Wicker, L. and Skamarock, W.: Time-splitting methods for elastic models using forward time schemes, Mon. Weather Rev., 130, 2088–2097, 2002. a
Williamson, J. H.: Low-Storage Runge-Kutta Schemes, J. Comput. Phys., 35, 48–56, https://doi.org/10.1016/0021-9991(80)90033-9, 1980. a, b
Wright, D. L., Kasibhatla, P. S., McGraw, R., and Schwartz, S. E.: Description and evaluation of a six-moment aerosol microphysical module for use in atmospheric chemical transport models, Journal of Geophysical Research: Atmospheres (1984–2012), 106, 20275–20291, https://doi.org/10.1029/2001JD900098, 2001. a
Xie, Z. and Castro, I. P.: LES and RANS for Turbulent Flow over Arrays of Wall-Mounted Obstacles, Flow Turbul. Combustion, 76, 291, https://doi.org/10.1007/s10494-006-9018-6, 2006. a
Young, K. C.: A Numerical Simulation of Wintertime, Orographic Precipitation: Part I. Description of Model Microphysics and Numerical Techniques., J. Atmos. Sci., 31, 1735–1748, https://doi.org/10.1175/1520-0469(1974)031<1735:ANSOWO>2.0.CO;2, 1974. a
Zaveri, R. A., Easter, R. C., Fast, J. D., and Peters, L. K.: Model for Simulating Aerosol Interactions and Chemistry (MOSAIC), J. Geophys. Res., 113, D13204, https://doi.org/10.1029/2007JD008782, 2008. a
Zhang, L., Gong, S., Padro, J., and Barrie, L.: A size-segregated particle dry deposition scheme for an atmospheric aerosol module, Atmos. Environ., 35, 549–560, https://doi.org/10.1016/S1352-2310(00)00326-5, 2001. a, b, c
Zhang, Y., Seigneur, C., Seinfeld, J. H., Jacobson, M. Z., and Binkowski, F. S.: Simulation of Aerosol Dynamics: A Comparative Review of Algorithms Used in Air Quality Models, Aerosol Sci. Tech., 31, 487–514, 1999. a, b
Zhang, Y., Pun, B., Vijayaraghavan, K., Wu, S., Seigneur, C., Pandis, S. N., Jacobson, M. Z., Nenes, A., and Seinfeld, J. H.: Development and application of the Model of Aerosol Dynamics, Reaction, Ionization, and Dissolution (MADRID), J. Geophys. Res., 109, D01202, https://doi.org/10.1029/2003JD003501, 2004. a, b
Zhao, Y., Saleh, R., Saliba, G., Presto, A. A., Gordon, T. D., Drozd, G. T., Goldstein, A. H., Donahue, N. M., and Robinson, A. L.: Reducing secondary organic aerosol formation from gasoline vehicle exhaust, P. Natl. Acad. Sci. USA, 114, 6984–6989, https://doi.org/10.1073/pnas.1620911114, 2017. a
Zhong, J., Cai, X.-M., and Bloss, W. J.: Coupling dynamics and chemistry in the air pollution modelling of street canyons: A review, Environ. Pollut., 214, 690–704, https://doi.org/10.1016/j.envpol.2016.04.052, 2016. a