the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Efficiency and robustness in Monte Carlo sampling for 3-D geophysical inversions with Obsidian v0.1.2: setting up for success
Richard Scalzo
David Kohn
Hugo Olierook
Gregory Houseman
Rohitash Chandra
Mark Girolami
Sally Cripps
The rigorous quantification of uncertainty in geophysical inversions is a challenging problem. Inversions are often ill-posed and the likelihood surface may be multi-modal; properties of any single mode become inadequate uncertainty measures, and sampling methods become inefficient for irregular posteriors or high-dimensional parameter spaces. We explore the influences of different choices made by the practitioner on the efficiency and accuracy of Bayesian geophysical inversion methods that rely on Markov chain Monte Carlo sampling to assess uncertainty using a multi-sensor inversion of the three-dimensional structure and composition of a region in the Cooper Basin of South Australia as a case study. The inversion is performed using an updated version of the Obsidian distributed inversion software. We find that the posterior for this inversion has a complex local covariance structure, hindering the efficiency of adaptive sampling methods that adjust the proposal based on the chain history. Within the context of a parallel-tempered Markov chain Monte Carlo scheme for exploring high-dimensional multi-modal posteriors, a preconditioned Crank–Nicolson proposal outperforms more conventional forms of random walk. Aspects of the problem setup, such as priors on petrophysics and on 3-D geological structure, affect the shape and separation of posterior modes, influencing sampling performance as well as the inversion results. The use of uninformative priors on sensor noise enables optimal weighting among multiple sensors even if noise levels are uncertain.
- Article
(5357 KB) -
Supplement
(732 KB) - BibTeX
- EndNote
Construction of 3-D geological models is plagued by the limitations on direct sampling and geophysical measurement (Wellmann et al., 2010; Lindsay et al., 2013). Direct geological observations are sparse because of the difficulty in acquiring them, with basement geology often obscured by sedimentary or regolith cover; acquiring direct observations at depth via drilling is expensive (Anand and Butt, 2010; Salama et al., 2016). Indirect observations via geophysical sensors deployed at or above the surface are more readily obtained (Strangway et al., 1973; Gupta and Grant, 1985; Sabins, 1999; Nabighian et al., 2005b, a). All geophysical measurements integrate data from the surrounding volume, so it is difficult to resolve precise geological constraints at any given position and depth, except where borehole measurements are also available. Determining the true underlying geological structure, or range of geological structures, consistent with observations constitutes an often poorly constrained inverse problem. One natural way to approach this is forward modeling, whereby the responses of various sensors on a proposed geological structure are simulated, and the proposed structure is then updated or sampled iteratively (for examples see Jessell, 2001; Calcagno et al., 2008; Olierook et al., 2015).
The incompleteness and uncertainty of the information contained in geophysical data frequently mean that there are many possible worlds consistent with the data being analyzed (Tarantola and Valette, 1982; Sambridge, 1998; Tarantola, 2005). To the extent that information provided by different datasets is complementary, combining all available information into a single joint inversion reduces uncertainty in the final results. Accomplishing this in a principled and self-consistent manner presents several challenges, including the following: (i) how to weigh constraints provided by different datasets relative to each other; (ii) how to rule out worlds inconsistent with geological processes (expert knowledge); (iii) how to present a transparent accounting of the remaining uncertainty; and (iv) how to do all this in a computationally efficient manner.
Bayesian statistical techniques provide a powerful framework for characterizing and fusing disparate sources of probabilistic information (Tarantola and Valette, 1982; Mosegaard and Tarantola, 1995; Sambridge and Mosegaard, 2002; Sambridge et al., 2012). In a Bayesian approach, model elements are flexible but all statements about the fit of a model, either to data or to preexisting expert knowledge, are expressed in terms of probability distributions; this forces the practitioner to make explicit all assumptions, not only about expected values or point estimates for system parameters, but also about their beliefs regarding the true values of those parameters. The output of a Bayesian method is also a probability distribution (the posterior) representing all values of system parameters consistent with both the available data and prior beliefs. For complex statistical models the exact posterior cannot be expressed analytically; in such cases, Monte Carlo algorithms, in particular Markov chain Monte Carlo (MCMC; Mosegaard and Tarantola, 1995; Sambridge and Mosegaard, 2002), can provide samples drawn from the posterior for the purpose of computing averages over uncertain properties of the system. The uncertainty associated with the posterior can be visualized in terms of the marginal distributions of parameters of interest or rendered in 3-D voxelizations of information entropy (Wellmann and Regenauer-Lieb, 2012). The inference also can be readily updated as new information becomes available using the posterior for the previous inference as the prior for the next one. This use of Bayesian updating allows for automated decision-making about which additional data to take to minimize the cost of reducing uncertainty (Mockus, 2013).
Although Bayesian methods provide rigorous uncertainty quantification, implementing them in practice for complicated forward models with many free parameters has proven difficult in other geoscientific contexts, such as landscape evolution (Chandra et al., 2019) and coral reef assembly (Pall et al., 2018). Sambridge and Mosegaard (2002) point out the challenge of capturing all elements of a geophysical problem in terms of probability, which can be difficult for complex datasets and even harder for approximate forward models or world representations in which the precise nature of the approximation is hard to capture. The irregular shapes and multi-modal structure of the posterior distributions for realistic geophysics problems make them hard to explore. The use of the inverse Fisher information matrix to describe posterior uncertainty implicitly assumes a single multivariate Gaussian mode; for posteriors with multiple modes or significant non-Gaussian tails, the inverse Fisher information provides only a lower bound on the posterior variance (Cramer, 1946; Rao, 1945) and may be a significant underestimate. Moreover, the large number of parameters needed to specify 3-D structures also means these irregular posteriors are embedded in high-dimensional spaces, increasing the computational cost for both optimization and sampling. Since the most appropriate sampling strategy may depend on the characteristics of the posterior for specific problems, sampling methods must usually be tailored to each individual problem and no “one-size-fits-all” solution exists (Green et al., 2015; Agostinetti and Malinverno, 2010; Bodin et al., 2012; Xiang et al., 2018).
While 1-D inversions for specific sensor types may use some quite sophisticated sampling methods (Agostinetti and Malinverno, 2010; Bodin et al., 2012; Xiang et al., 2018), the uptake of MCMC sampling appears to be slower for 3-D structural modeling problems. Giraud et al. (2016) and Giraud et al. (2017, 2018) demonstrate an optimization-based Bayesian inversion framework for 3-D geological models, which finds the maximum of the posterior distribution (maximum a posteriori, or MAP); while they show that fusing data reduces uncertainty around this mode, they do not attempt to find or characterize other modes, and only Giraud et al. (2016) calculate the actual posterior covariance. Ruggeri et al. (2015) investigate several MCMC schemes for sampling a single-sensor inverse problem (cross-hole georadar travel time tomography), focusing on sequential, localized perturbations of a proposed 3-D model (sequential geostatistical resampling, or SGR); they show that sampling is impractically slow due to high dimensionality and correlations between model parameters. Laloy et al. (2016) embed the SGR proposal within a parallel-tempered sampling scheme to explore multiple posterior modes of a 2-D inverse problem in groundwater flow, improving computational performance but not to a cost-effective threshold.
The above methods are nonparametric in that the model parameters simply form a 3-D field of rock properties to which sensors respond. Although this type of method is flexible, parametric models, in which the parameterized elements correspond more directly to geological interpretation, comprise a more transparent and parsimonious approach. Wellmann et al. (2010) describe a workflow for propagating uncertainty in structural data through to uncertainty in the geological interpretation. Pakyuz-Charrier et al. (2018b, a) further develop a Monte Carlo approach to uncertainty estimation for structural and drill hole data, showing the impact of different distributions used to summarize uncertainty in the data. Such approaches are much simplified by the use of an implicit potential-field parameterization of geological structure (Lajaunie et al., 1997), in which the data coincide directly with model parameters; conditioning on further data, and hence the use of MCMC methods, is not necessary in this context. de la Varga and Wellmann (2016) and de la Varga et al. (2019) recast the modeling of structural data in terms of MCMC sampling of a posterior, which is required in order to fuse structural data with other types of data, including geophysical sensor data. A large-scale 3-D joint inversion with multiple sensors remains to be done in this framework.
McCalman et al. (2014) present Obsidian, a flexible software platform for MCMC sampling of 3-D multi-modal geophysical models on distributed computing clusters. Beardsmore (2014) and Beardsmore et al. (2016) demonstrate Obsidian on a test problem in geothermal exploration in the Moomba gas field of the Cooper Basin in South Australia and compare their results to a deterministic inversion of the same area performed by Meixner and Holgate (2009). These papers outline a full-featured open-source inversion method that can fuse heterogeneous data into a detailed solution, but they make few comments about how the efficiency and robustness of the method depend on the particular choices they made.
In this paper, we revisit the inversion problem of Beardsmore et al. (2016) using a customized version (Scalzo et al., 2019) of the McCalman et al. (2014) inversion code. Our interest is in exploring this problem as a case study to determine which aspects of this problem's posterior present the most significant obstacles to efficient sampling, which updates to the MCMC scheme improve sampling under these conditions, and how plausible alternative choices of problem setup might influence the efficiency of sampling or the robustness of the inversion. The aspects we consider include correlations between model parameters, relative weights between datasets with poorly constrained uncertainty, and degrees of constraint from prior knowledge representing different possible exploration scenarios.
In this section we present a brief overview of the Bayesian forward-modeling paradigm to geophysical inversions. We also provide a discussion on implementing Bayesian inference via sampling using MCMC methods. We then present the background of the original Moomba inversion problem, commenting on choices made in the inversion process before we begin to explore different choices in subsequent sections.
2.1 Overview of Bayesian inversion
A Bayesian inversion scheme for geophysical forward models is comprised of three key elements:
-
the underlying parameterized representation of the simulated volume or history, which we call the world or world view, denoted by a vector of world parameters ;
-
a probability distribution p(θ) over the world parameters, called the prior, expressing expert knowledge or belief about the world before any datasets are analyzed; and
-
a probability distribution p(𝒟|θ) over possible realizations of the observed data 𝒟 as a function of world parameters, called the likelihood, that incorporates the prediction of a deterministic forward model g(θ) of the sensing process for each value of θ.
The posterior is then the distribution p(θ|𝒟) of the values of the world parameters consistent with both prior knowledge and observed data. Bayes' theorem describes the relationship between the prior, likelihood, and posterior:
Although each of these elements has a correspondence to some similar model element in more traditional geophysical inversion literature (for example, Menke, 2018), interpreting model elements in terms of probability may motivate different mathematical choices from the usual non-probabilistic misfit or regularization terms. The terminology we use in this paper will be typical of the statistics literature. In other geophysical inversion papers a “model” might refer to the world representation, whereas below we will use the word “model” to refer to the statistical model defined by a choice of parameterization, prior, and likelihood. A non-Bayesian inversion would proceed by minimizing an objective function, one simple form of which is the mean square misfit between the (statistical) model predictions and the data, corresponding to our negative log likelihood (assuming observational errors that are independent and Gaussian-distributed with precisely known variance). To penalize solutions that are considered a priori unlikely, the objective function might include additional regularization terms corresponding to the negative log priors in our framework; the weight of a non-probabilistic regularization term might ordinarily be optimized by cross-validation against subsets of the data (MacCarthy et al., 2011; Wrona et al., 2018), whereas in our framework we include plausible (possibly vague) constraints as part of the prior distribution. The full objective function would correspond to the negative log posterior, and minimization of the objective function would correspond to maximization of the posterior probability, under some choice of prior.
Indeed, there is considerable flexibility in choosing the above elements even in a fully probabilistic context. For example, the partitioning of information into “data” and “prior knowledge” is neither unique nor cut-and-dried. However, there are guiding principles: the ideal set of parameters θ is both parsimonious – as few as possible to faithfully represent the world – and interpretable, referring to meaningful aspects of the world that can easily be read off the parameter vector. Information resulting from processes that can be easily simulated belongs in the likelihood: for example, one might argue that the output of a gravimeter should have a Gaussian distribution because it responds to the mean rock density within a volume and hence obeys the central limit theorem or that the output of a Geiger counter should follow a Poisson distribution to reflect the physics of radioactive decay. Even processes that are not so easily simulated can at least be approximately described, for example by using a mixture distribution to account for outlier measurements (Mosegaard and Tarantola, 1995) or a prior on the unknown noise level in a process (Sambridge et al., 2012). Other information about allowable or likely worlds belongs in the prior, such as the distribution of initial conditions for simulation or interpretations of datasets with expensive or intractable forward models.
The implicit assumption behind the use of mean square error as a (log) likelihood – that the residuals of the data for each sensor from the corresponding forward model are independent Gaussian – may not be true if the data have been interpolated, resampled, or otherwise modified from original point observations. For example, gravity anomaly and magnetic anomaly measurements are usually taken at ground level along access trails to a site or along spaced flight lines in the case of aeromagnetics. In online data releases, the original measurements may then be interpolated or resampled onto a grid, changing the number and spacing of points and introducing correlations on spatial scales comparable to the scale of the smoothing kernel. This resampling of observations onto a regular grid may be useful for traditional inversions using Fourier transform techniques. However, if used uncritically in a Bayesian inversion context, correlations in residuals from the model may then arise from the resampling process rather than from model misfit, resulting in stronger penalties in the likelihood for what would otherwise be plausible worlds and muddying questions around model inadequacy. If such correlations are known to exist, they can be modeled explicitly as part of the likelihood. For example, autoregressive models are already being used as error models for 1-D inversions of magnetotelluric and seismic data (Agostinetti and Malinverno, 2010; Bodin et al., 2012; Xiang et al., 2018). Care must be taken in formulating such likelihoods to avoid confusion between real (but possibly unresolved) structure and correlated observational noise.
The inference process expresses its results in terms of either p(θ|𝒟) itself or integrals over p(θ|𝒟) (including credible limits on θ). This is different from the use of point estimates for the world parameters, such as the maximum likelihood (ML) solution or the maximum a posteriori (MAP) solution . To the extent that ML or MAP prescriptions give any estimate of uncertainty on θ, they usually do so through the covariance of the log likelihood or log posterior around the optimal value of θ, equivalent to a local approximation of the likelihood or posterior by a multivariate Gaussian. As mentioned above, these approaches will underestimate the uncertainty for complex posteriors; a more rigorous accounting of uncertainty will include all known modes, higher moments of the distribution, or (more simply) enough samples from the distribution to characterize it.
The posterior distribution p(θ|𝒟) is rarely available in closed form. However, it is often known up to a normalizing constant: p(𝒟|θ)p(θ). Sampling methods such as MCMC can therefore be used to approximate the posterior without having to explicitly evaluate the normalizing constant (the high-dimensional integral in the denominator of Eq. 1). It is to these methods we turn next.
2.2 Markov chain Monte Carlo
An MCMC algorithm comprises a sequence of world parameter vectors {θ[j]}, called a (Markov) chain, and a proposal distribution to generate a new set of parameters based only on the last element of the chain. In the commonly used Metropolis–Hastings algorithm (Metropolis et al., 1953; Hastings, 1970), a proposal is at random either accepted and added to the chain's history () with probability
or it is rejected and a copy of the previous state added instead (). This rule guarantees, under certain regularity conditions (Chib and Greenberg, 1995), that the sequence {θ[j]} converges to the required stationary distribution, P(θ|𝒟), in the limit of increasing n.
Metropolis–Hastings algorithms form a large class of sampling algorithms limited only by the forms of proposals. Although proofs that the chain will eventually sample from the posterior are important, clearly chains based on efficient proposals are to be preferred. A proposal's efficiency will depend on the degree of correlation between consecutive states in the chain, which in turn can depend on how well matched the proposal distribution is to the properties of the posterior.
One simple, commonly used proposal distribution is a (multivariate) Gaussian random walk (GRW) step u from the chain's current position, drawn from a multivariate Gaussian distribution with covariance matrix Σ:
This proposal is straightforward to implement, but its effectiveness can depend strongly on Σ and does not in general scale well to rich, high-dimensional world parameterizations. If Σ has too large a scale, the GRW proposal will step too often into regions of low probability, resulting in many repeated states due to rejections; if the scale is too small, the chain will take only small, incremental steps. In both cases, subsequent states are highly correlated. If the shape of Σ is not tuned to capture correlations between different dimensions of θ, the overall scale must usually be reduced to ensure a reasonable acceptance fraction. If constraints from additional data are weak, Σ could take the shape of the prior; if there are no other constraints, as in Monte Carlo uncertainty estimation (MCUE) (Pakyuz-Charrier et al., 2018b, a), sampling directly from the prior may be easier.
The SGR method (Ruggeri et al., 2015; Laloy et al., 2016) can be seen as a mixture of multivariate Gaussians, in which Σ has highly correlated sub-blocks of parameters corresponding to variations of the world over different spatial scales. Ruggeri et al. (2015) and Laloy et al. (2016) evaluate SGR using single-sensor inversions in cross-hole georadar travel time tomography, with posteriors corresponding to a Gaussian process – an unusually tractable (if high-dimensional) problem that could be solved in closed form as a cross-check. These authors found that in general updating blocks of parameters simultaneously was inefficient, which may not be surprising in a high-dimensional model: for a tightly constrained posterior lying along a low-dimensional subspace of parameter space, almost all directions – and hence almost all posterior covariance choices – lead towards regions of low probability. Directions picked at random without regard for the shape of the posterior will scale badly with increasing dimension.
Many other types of proposals can be used in Metropolis–Hastings sampling schemes with information from ensembles of particles (Goodman and Weare, 2010, as distinct from particle swarm optimization or sequential Monte Carlo), the adaptation of the proposal distribution based on the chain's history (Haario et al., 2001), derivatives of the posterior (Neal, 2011; Girolami and Calderhead, 2011), approximations to the posterior (Strathmann et al., 2015), and so forth. The GRW proposal is not only easy to write down and fast to evaluate, but also requires no derivative information. We will compare and contrast several derivative-free proposals in our experiments below.
The posterior distributions arising in geophysical inversion problems are also frequently multi-modal; MCMC algorithms to sample such posteriors need the ability to escape from, or travel easily between, local modes. Parallel-tempered MCMC, or PTMCMC (Geyer and Thompson, 1995), is a meta-method used by Obsidian for sampling multi-modal distributions that works by running an ensemble of Markov chains. The ensemble is characterized by a sequence of M+1 parameters {βi}, with , called the (inverse) temperature ladder. Each chain samples the distribution
so that the chain with β0=1 is sampling from the desired posterior and a chain with βi=0 samples from the prior, which should be easy to explore. Chains with intermediate values sample intermediate distributions in which the data's influence is reduced so that modes are shallower and easier for chains to escape and traverse. In addition to proposing new states within each chain, PTMCMC includes Metropolis-style proposals that allow for adjacent chains on the temperature ladder, with inverse temperatures β and β′, to swap their most recent states θ and θ′ with probability
This allows chains with current states spread throughout parameter space to share global information about the posterior in such a way that chain i still samples Pi(θ|D) in the long-term limit. The locations of discovered modes diffuse from low-βi chains (which can jump freely between relaxed, broadened versions of these modes) towards the β0=1 chain, which can then sample from all modes of the unmodified posterior in the correct proportions. The temperature ladder should be defined so that adjacent chains on the ladder are sampling from distributions similar enough for swaps to occur frequently.
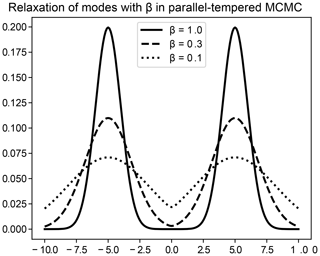
Figure 1 illustrates the sampling of a simple bimodal probability distribution (a mixture of two Gaussians) via PTMCMC. The solid line depicts the true bimodal distribution, while the broken lines show the stationary distribution of tempered chains for smaller values of β. The tempered chains are more likely to propose moves across modes than the untempered chains, and the existence of a sequence of chains ensures that the difference in probability between successive chains is small enough that swaps can take place easily.
Since only samples from the β=1 chain are retained as samples from the true posterior, and since the time for information about well-separated modes to propagate down the ladder increases as the square of the number of inverse temperatures used, PTMCMC can be extremely computationally intensive. It should be employed only in cases in which multiple modes are likely to be present and when capturing the relative contributions of all of these modes is relevant to the application. For problems that have many deep, well-separated modes (e.g., Chandra et al., 2019), swap proposals may provide the only source of movement in the low-temperature chains; such posteriors present next-generation challenges for sampling.
Even without regard to multiple modes, PTMCMC can also help to reduce correlations between successive independent posterior samples. Laloy et al. (2016) use SGR as a within-chain proposal in a PTMCMC scheme, demonstrating its effects on correlations between samples but noting that the algorithm remains computationally intensive.
2.3 Performance metrics for MCMC
Because MCMC guarantees results only in the limit of large samples, criteria are still required to assess the algorithm's performance. Suppose for the discussion below that up to the assessment point, we have obtained N samples of a d-dimensional posterior from each of M separate chains; let be the d×1 vector of parameter values drawn at iteration [j] in chain i. Let
be the mean value of the parameter θk in chain i across the N iterates, and let be the sample mean of θk across all iterates and chains. Then
Further define
and
For Metropolis–Hastings MCMC, the acceptance fraction of proposals is easily measured and for a chain that is performing well should be ∼20 %–50 %. Roberts et al. (1997) showed that the optimal acceptance fraction for random walks in the limit of a large number of dimensions is 0.234, which we will take as our target since the proposals we will consider are modified random walks.
We examine correlations between samples within each chain separated by a lag time l using the autocorrelation function,
The number of independent draws from the posterior with equal statistical power to each set of N chain samples scales with the area under the autocorrelation function or (integrated) autocorrelation time,
A trace plot of the history of an element of the parameter vector θ over time summarizes the sampling performance at a glance, revealing where in parameter space an algorithm is spending its time; Fig. 3 shows a series of such figures for some of the different MCMC runs in the present work.
Gelman and Rubin (1992) assess the number of samples required to reach a robust sampling of the posterior by comparing results among multiple chains. If the simulation has run long enough, the mean values among chains should differ by some small fraction of the width of the distribution; intuitively, this is similar to a hypothesis test that the chains are sampling the same marginal distribution for each parameter. More precisely, the quantity
provides a metric for the convergence of different chains to the same result, which decreases to 1 as N→∞. The chains may be stopped and results read out when the metric dips below a target value for all world parameters θ. The precise number of samples needed may depend on the details of the distribution; the metric provides a stopping condition but not an estimate of how long it will take to achieve.
The results from this procedure must still be evaluated according to how well the underlying statistical model describes the geophysical data and whether the results are geologically plausible – although this is not unique to MCMC solutions. The distribution of residuals of model predictions (forward-modeled datasets) from the observed data can be compared to the assumed likelihood. The standard deviation or variance of the residuals (relative to the uncertainty) provides a convenient single-number summary, but the spatial distribution of residuals may also be important; outliers and/or structured residuals will indicate places where the model fails to predict the data well and highlight parts of the model parameterization that need refinement.
Finally, representative instances of the world itself should be visualized to check for surprising features. Given the complexity of real-world data, the adequacy of a given model is in part a matter of scientific judgment or fitness for a particular applied purpose to which the model will be put. We will use the term model inadequacy to refer to model errors arising from approximations or inaccuracies in the world parameterization or the mathematical specification of the forward model – although there will always be such approximations in real problems, and the presence of model inadequacy should not imply that the model is unfit for purpose.
2.4 The Obsidian distributed PTMCMC code
For our experiments we use a customized fork (v0.1.2; Scalzo et al., 2019) of the open-source Obsidian software package. Obsidian was previously presented in McCalman et al. (2014) and was used to obtain the modeling results of Beardsmore et al. (2016); v0.1.1 was the most recent open-source version publicly available before our work. We refer the reader to these publications for a comprehensive description of Obsidian, but below we summarize key elements corresponding to the inversion framework set out above and describe the changes we have made to the code since v0.1.1.
Obsidian was designed to run on large distributed architectures such as supercomputing clusters. McCalman et al. (2014) show that the code scales well to large numbers of processors by allowing individual MCMC chains to run in parallel and initiating communication between chains only when a PTMCMC swap proposal is initiated. The inversion of Beardsmore et al. (2016) was performed on Amazon Web Services using 160 cores.
2.4.1 World parameterization
Obsidian's world is parameterized as a series of discrete units, each with its own spatially constant rock properties separated by smooth boundaries. Each unit boundary is defined by a set of control points that specify the subsurface depth of the boundary at given surface locations. The depth to each unit boundary at any other location is calculated using a two-dimensional Gaussian process regression (kriging) through the control points; each unit is truncated against the overlying unit to allow for the lateral termination of units and ensure a strict stratigraphic sequence.
For a world with N units, indexed by i with , each with a grid ni of regularly spaced control points at sites xi and with K rock properties necessary and sufficient to evaluate the forward models for all relevant sensors, the parameter vector is therefore
where αij is the offset of the mean depth of the top of unit i at site j, and ρis is the rock property of unit i associated with sensor s. Taken together, the rock properties for each unit and the control points for the boundaries between the units fully specify the world. This parameterization requires that interface depths be single-valued, not, for example, permitting the surface to fold above or below. Such a limitation still enables reasonable representations of sedimentary basins but may hinder faithful modeling of other kinds of structures.
2.4.2 Prior
The control point depth offsets within each unit i have a multivariate Gaussian prior with mean zero and covariance . The Gaussian processes that interpolate the unit boundaries across the lateral extent of the world use a radial basis function kernel to describe the correlation structure of the surface between two surface locations (x,y) and ,
and have a mean function μi(x,y) that can be specified at finer resolution to capture fine detail in unit structure. The correlation lengths Δx and Δy could in principle be varied, but in this case they are fixed in value to the spacing between control point locations along the x and y coordinate axes, respectively. The rock properties for each unit i, which are statistically independent of the control points, also have a multivariate Gaussian prior, with mean and covariance . This allows the user to formulate priors that capture intrinsic covariances between rock properties, though of a somewhat simpler form than the petrophysical mixture models of Giraud et al. (2017). The prior for the full parameter vector is therefore block diagonal:
2.4.3 Likelihood
The likelihood for each Obsidian sensor s is Gaussian, meaning that the residuals of the data 𝒟s={dsi} from the forward model predictions {fsi(θ)} for the true world parameters θ are assumed to be independent, identically distributed Gaussian draws. The underlying variance of the Gaussian noise is not known but is assumed to follow an inverse gamma distribution with different (user-specified) hyperparameters αs and βs for each sensor s. This choice of distribution amounts to a prior, but the hyperparameters αs and βs for each sensor are not explicitly sampled over; instead, they are integrated out analytically so that the final likelihood has the form
where tν(x) is a Student's t distribution with ν degrees of freedom. This distribution is straightforward to calculate, although the results may be sensitive to the user's choices of αs and βs; unrestrictive choices (e.g., ) should be used if the user has little prior knowledge about the noise level in the data. The likelihood including all sensors is therefore
since each sensor probes a different physical aspect of the rock. Obsidian v0.1.1 includes forward models for gravity and magnetic anomaly, magnetotellurics, reflection seismic, thermal, and contact-point sensors for drill cores; v0.1.2 introduces a lithostratigraphic sensor.
2.4.4 MCMC
The sampling algorithm used by Obsidian is an adaptive form of PTMCMC, described in detail in Miasojedow et al. (2013). This algorithm allows for the progressive adjustment of the step size used for proposals within each chain, as well as the temperature ladder used to sample across chains, as sampling progresses. A key feature of the adjustment process is that the maximum allowed change to any chain property diminishes over time, made inversely proportional to the number of samples; this is necessary to ensure that the chains converge to the correct distribution in the limit of large numbers of samples (Roberts and Rosenthal, 2007). The Obsidian implementation of PTMCMC also allows it to be run on distributed computing clusters, making it truly parallel in resource use as well as in the requirement for multiple chains. Obsidian v0.1.2 uses the same methods for adapting the PTMCMC temperature ladder and the sizes of within-chain proposals as v0.1.1, but it adds new options for within-chain proposal distributions (see Sect. 3.1 below).
2.5 The original Moomba inversion problem
The goal of the original Moomba inversion problem (Beardsmore, 2014; Beardsmore et al., 2016; McCalman et al., 2014) was to identify potential geothermal energy applications from hot granites in the South Australian part of the Cooper Basin (see Carr et al., 2016, for a recent review of the Cooper Basin). Modeling the structure of granite intrusions and their temperature enabled the inference of the probability of the presence of granite above 270 ∘C at any point within the volume. The provenance of the original datasets involved, and how they were used to set up the prior for the original inversion, is described in more detail in the final technical report published by NICTA (Beardsmore, 2014), while the results are described in the corresponding conference paper (Beardsmore et al., 2016); we summarize key elements in this section as appropriate.
The chosen region was a portion of the Moomba gas field with dimensions of 35 km × 35 km × 12 km volume centered at −28.1∘ S, 140.2∘ E. The volume is divided into six layers, with the first four being thin, sub-horizontal, Permo–Triassic sedimentary layers, the fifth corresponding to Carboniferous–Permian granitoid intrusions (Big Lake Suite), and the sixth to a Proterozoic basement (Carr et al., 2016). The number of layers and the priors on mean depths of layer boundaries were related to interpretations of depth-converted seismic reflection horizons published by the Department of State Development (DSD) in South Australia (Beardsmore et al., 2016). Data used in the original inversion include Bouguer anomaly, total magnetic intensity, magnetotelluric sensor data at 44 frequencies between 0.0005 and 240 Hz, temperature measurements from gas wells, and petrophysical laboratory measurements based on 115 core samples from holes drilled throughout the region. Rock properties measured for each sample include density, magnetic susceptibility, thermal conductivity, thermal productivity, and resistivity.
The original choices of how to partition knowledge between prior and likelihood struck a balance between the accuracy of the world representation and computational efficiency. The empirical covariances of the petrophysical sample measurements for each layer were used to specify a multivariate Gaussian prior on that layer's rock properties; although these measurements could be construed as data, the simplifying assumption of spatially constant mean rock properties left little reason to write their properties into the likelihood. The gravity, magnetic, magnetotelluric, and thermal data all directly constrained rock properties relevant to the geothermal application and were explicitly forward-modeled as data. “Contact points” from drilled wells, directly constraining the layer depths in the neighborhood of a drilled hole as part of the likelihood, were available and used to inform the prior but were not treated as sensors in the likelihood. Treating the seismic measurements as data would have dramatically increased computational overhead relative to the use of interpreted reflection horizons as mean functions for layer boundary depths in the prior. Using interpreted seismic data to inform the mean functions of the layer boundary priors also reduced the dimension of the parameter space, letting the control points specify long-wavelength deviations from seismically derived prior knowledge at finer detail: each reflection horizon was interpolated onto a 20×20 grid.
Given this knowledge of the local geology (Carr et al., 2016; Beardsmore, 2014; McCalman et al., 2014), the world parameters for geometry were chosen as follows: the surface was fixed by a level plane at zero depth. The control point grids for the relatively simple sedimentary layers were specified by 2×2 grids of control points (lateral spacing: 17.5 km). The layer boundary for the granite intrusion layer used a 7×7 grid (lateral spacing: 5 km) and also underwent a nonlinear transformation stretching the boundary vertically to better represent the elongated shapes of the intrusions. Including the rock properties, this allowed the entire world to be specified by a vector of 101 parameters, which is a large but not unmanageable number.
Figure 4 shows horizontal slices through the posterior probability density for granite at a depth of 3.5 km, similar to that shown in Fig. 9 of Beardsmore et al. (2016), for three MCMC runs sampling from the original problem. While the posterior samples from the previous inference are not available for quantitative comparison, we see reasonable qualitative agreement with previous results in the cross-sectional shape of the granite intrusion.
To demonstrate the impact of problem setup and proposal efficiency in a Bayesian MCMC scheme for geophysical inversion, we run a series of experiments altering the prior, likelihood, and proposal for the Moomba problem. We approach this variation as an iterative investigation into the nature of the data and the posterior's dependence on them, motivating each choice with the intent of relating our findings to related 3-D inversion problems.
The experiments described in this section were run on the Artemis high-performance computing cluster at the University of Sydney. Artemis's standard job queue provides access to 56 nodes with 24 Intel Xeon E5-2680-V3 (2.5 GHz) cores each and 80 nodes with 32 Intel Xeon E5-2697A-V4 (2.6 GHz) cores each. Each run used 32 cores and ran for up to 8 h of wall time.
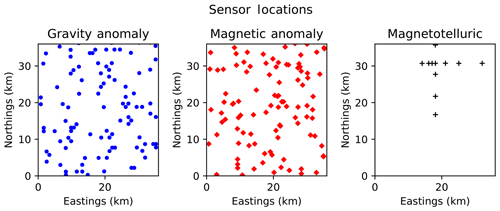
The datasets we use for our experiments are the gravity anomaly, total magnetic intensity, and magnetotelluric readings originally distributed as an example Moomba configuration with v0.1.1 of the Obsidian source code. In order to focus on information that may be available in an exploration context (i.e., publicly available geophysical surveys without contact points), we omit the thermal sensor readings relying on a joint inversion of gravity, magnetic, and magnetotelluric data. Maps of the locations of these sensor readings, referring to the coordinate system of the inversion, are shown in Fig. 2.
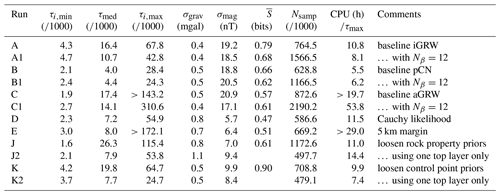
All experiments use PTMCMC sampling, with 4 simultaneous temperature ladders or “stacks” of chains, each with 8 temperatures unless otherwise specified. The posterior is formally defined in terms of samples over the world parameters, so when quantifying predictions for particular regions of the world and their uncertainty (such as entropy), the parameter samples are each used to create a voxelized realization of the 3-D world and the average observable calculated over these voxelized samples. A quantitative summary of our results is shown in Table 1, including the following for each run:
-
the shortest (τmin), median (τmed), and longest (τmax) autocorrelation time measured for individual model parameters;
-
the standard deviations, σgrav and σmag, of the gravity and magnetic anomaly sensor data from the posterior mean forward model prediction in physical units;
-
the mean information entropy (Shannon, 1948; Wellmann and Regenauer-Lieb, 2012) of the posterior probability density for granite, averaged over the volume beneath 3.5 km, in bits (i.e., the presence or absence of granite; an entropy of 0 bits means total certainty, while 1 bit of entropy indicates total uncertainty) – this measure is appropriate to summarize posterior uncertainty in categorical predictions such as the type of rock; and
-
the CPU time spent per worst-case autocorrelation time as a measure of computational efficiency.
Table 1Performance metrics for each run, including the following: best-case (τi,min), median (τi,med), and worst-case (τi,max) autocorrelation times for model parameters; standard deviations, σgrav and σmag, of residuals of the posterior mean forward model predictions for the gravity anomaly and magnetic anomaly data; volume-average information entropy ; number of chain iterates Nsamples (with each iterate representing a single evaluation of all forward models for a given set of world parameters); and CPU hours per autocorrelation time (i.e., the computational cost of obtaining a single independent sample from the posterior).
3.1 Choice of within-chain proposal
The initial work of McCalman et al. (2014) and Beardsmore et al. (2016) used an isotropic Gaussian random walk (iGRW) proposal within each chain:
where η is a (possibly adaptive) step size parameter tuned to reach a target acceptance rate, which we choose to be 25 % for our experiments. Each dimension of a sampled parameter vector is “whitened” by dividing it by a scale factor corresponding to the allowed full range of the variable (of the order of a few times the prior width; this also accounts for differences in physical units between parameters). This should at least provide a scale for the marginal distribution of each parameter but does not account for potential correlations between parameters. The covariance matrix of the iGRW proposal is a multiple of the identity matrix so that, on average, steps of identical extent are taken along every direction in parameter space. When tuning the proposal, the adaptive scheme tunes only an overall step size applying to all dimensions at once.
The iGRW proposal is the simplest proposal available, but as noted above, it loses efficiency in high-dimensional parameter spaces, and it is unable to adapt if the posterior is highly anisotropic – for example, if parameters are scaled inappropriately or are highly correlated. To maintain the target acceptance rate, the adapted step size approaches the scale of the posterior's narrowest dimension, and the random walk will then slowly explore the other dimensions using this small step size. The time it takes for a random walk to cover a distance scales as the square of that distance, so we might expect the worst-case autocorrelation time for random walk MCMC in a long, narrow mode to scale as the condition number of the covariance matrix for that mode.
The adaptive (anisotropic) Gaussian random walk (Haario et al., 2001), or aGRW, attempts to learn an appropriate covariance structure for a random walk proposal based on the past history of the chain. The covariance of the aGRW proposal is calculated in terms of the sample covariance of the chain history {θ[j]}:
in which
where a is a timescale for adaptation (measured in samples). As the length n of the chain increases, the proposal will smoothly transition from an isotropic random walk to an anisotropic random walk with a covariance structure that reflects the chain history.
A third proposal, addressing high-dimensional parameter spaces, is the preconditioned Crank–Nicolson (pCN) proposal (Cotter et al., 2013):
with and P(θ) as a multivariate Gaussian prior. For η≪1, the proposal resembles a GRW proposal with small step size, while for η∼1 the proposal becomes a draw from the prior. This proposal results in a sampling efficiency that is independent of the dimensionality of θ; in fact, it was developed by Cotter et al. (2013) to sample infinite-dimensional function spaces arising in inversion problems using differential equations as forward models, wherein the prior is specified in the eigenbasis for the forward model operator. In our case, the prior incorporates the correlation between neighboring control points in the Gaussian process layer boundaries, so we might expect a proposal that respects this structure to improve sampling.
Our first three runs (A, B, C) use the iGRW, pCN, and aGRW (with a=10) proposals, respectively. All three algorithms give roughly similar results on the baseline dataset. The autocorrelation time for this problem remains very long, of the order of 104 samples. This means that ∼106 samples are required to achieve reasonable statistical power.
There are nevertheless differences in efficiency among the samplers. The pCN proposal has not only the lowest median autocorrelation, but also the lowest worst-case autocorrelation across dimensions. The aGRW proposal has the largest spread in autocorrelation times across dimensions, with its median performance comparable to iGRW and its worst-case performance at least 3 times worse (it had still failed to converge after over 1000 h of CPU time). Repeat trials running for twice as many samples with 12 chains per stack instead of 8 (runs A1, B1, C1) produced similar results, although we were then able to reliably measure the worst-case autocorrelation time for aGRW. For all samplers, but most noticeably aGRW, the step size can take a long time to adapt. Large differences are sometimes seen in the adapted step sizes between chains at similar temperatures in different stacks and do not always increase monotonically with temperature.
The differences are shown in Fig. 3, showing the zero-temperature chains from the four stacks in each run sampling the marginal distribution of the rock density for layer 3, a bimodal parameter. The iGRW chains converge slowly, and though they manage to travel between modes with the help of parallel-tempered swap proposals, the relative weights of the two modes are not fully converged and vary between reruns at a fixed length. Each aGRW chain has a relatively narrow variance and none successfully crosses over to the high-density mode despite parallel-tempered swaps. Only the pCN chains converge “quickly” (after about 70 000 samples) and are able to explore the full width of the distribution.
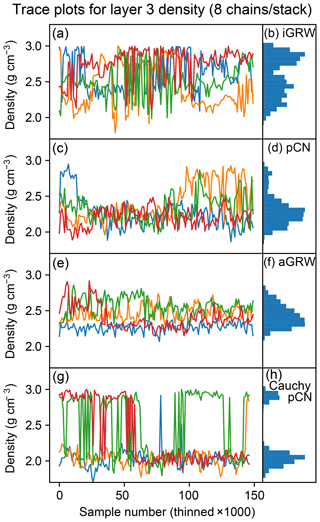
Figure 3Trace plots (a, c, e, g) and marginal densities (b, d, f, h) for layer 3 rock density as explored by iGRW, pCN, and aGRW proposals, as well as by a pCN proposal under a Cauchy likelihood (top to bottom). The four colors represent the four different chains.
These behaviors suggest that the local shape of the posterior varies across parameter space, so proposals that depend on a global fixed scaling across all dimensions are unlikely to perform well. The clearly superior performance of pCN for this problem is nevertheless intriguing, since for a sufficiently small step size near β=1, the proposal reduces to GRW.
The different proposals vary in performance when hopping between modes despite the fact that all three proposals are embedded within a PTMCMC scheme with a relatively simple multivariate Gaussian prior, to which aGRW should be able to adapt readily. We believe pCN will prove to be a good baseline proposal for tempered sampling of high-dimensional problems because of its prior-preserving properties, which ensure peak performance when constraints from the data are weak. As the chain temperature increases, the tempered posterior density approaches the prior so that pCN proposals with a properly adapted step size will smoothly approach independent draws from the prior with an acceptance probability of 1. The result is that when used as the within-chain proposal in a high-dimensional PTMCMC algorithm, pCN proposals will result in near-optimal behavior for the highest-temperature chain and should explore multiple modes much more easily than GRW proposals.
This behavior stands in contrast to GRW proposals, for which the acceptance fraction given any particular tuning will approach zero as the dimension increases. In fact, aGRW's attempt to adapt globally to proposals with local structure may mean mid-temperature chains become trapped in low-probability areas and break the diffusion of information down to lower temperatures from the prior. A more detailed study of the behavior of these proposals within tempered sampling schemes would be an interesting topic for future research.
3.2 Variations in likelihood and noise prior
In the fiducial Moomba configuration used in Beardsmore et al. (2016), the priors on the unknown variance of the Gaussian likelihood for each sensor are relatively informative. The uncertainty on the variance of a sensor is determined by the α parameter in that sensor's prior, with smaller α corresponding to more uncertainty. For example, the gravity and magnetotelluric sensors use a prior with α=5 so that the resulting t distribution for model residuals in the likelihood has degrees of freedom. The magnetic anomaly sensor prior uses α=1.25, resulting in a residual distribution with thick tails closer to a Cauchy distribution than a Gaussian.
If specific informative prior knowledge about observational errors exists, using such a prior, or even fixing the noise level outright, makes sense. In cases in which the amplitude of the noise term is not well constrained, using a broader prior on the noise term may be preferable. When more than one sensor with unknown noise variance is used, identical broad priors allow the data to constrain the relative influence of each sensor on the final results. The trade-off is that a more permissive prior on the noise variance could mask structured residuals due to model inadequacy or non-Gaussian outliers in the true noise distribution.
The idea that such broad assumptions could deliver competitive results arises from the incorporation of Occam's razor into Bayesian reasoning, as demonstrated in Sambridge et al. (2012). For example, the log likelihood corresponding to independent Gaussian noise is
Ordinary least-squares fitting maximizes the left-hand term inside the sum, and the right-hand term is a constant that can be ignored if the observational uncertainty σ is known. This clearly penalizes worlds θ, resulting in large residuals. Suppose that σ is not perfectly known a priori, however (but is still assumed to be the same for all points in a single sensor dataset), and is allowed to vary alongside θ: the left-hand term penalizes small (overly confident) values of σ, while the right-hand term penalizes large values of σ, corresponding to an assumption that the data are entirely explained by observational noise.
Typical residuals from the Beardsmore et al. (2016) inferences correspond to about 10 % of the dataset's full range, so we next perform a run in which the noise prior is set to α=0.5 and β=0.05 for all sensors (gravity, magnetic, and magnetotelluric). The corresponding likelihood (with the noise variance prior integrated out) becomes a Cauchy (or t1) distribution, with thick tails that allow for substantial outliers from the core. This choice of α and β thus also allows us to make contact with prior work in which Cauchy distributions have been used (Silva and Cutrim, 1989; de la Varga et al., 2019): a Gaussian likelihood with unknown, IG(0.5,βs)-distributed variance is mathematically equivalent to a Cauchy likelihood with known scale 2βs. The two choices are conceptually different, since in the Gaussian case outliers appear when the wrong variance scale is applied, whereas in the Cauchy case the scale is assumed known and the data have an intrinsically heavy-tailed distribution.
Under this new likelihood the residuals from the gravity observations increase (by about a factor of 1.5–2), while the residuals from the magnetic sensors decrease (by a factor of 3–4). This rebalancing of residuals among the sensors with an uninformative prior can be used to inform subsequent rounds of modeling more readily.
The inference also changes: in run D, a granite bridge runs from the main outcrop to the eastern edge of the modeled volume, with the presence of granite in the northwest corner being less certain. Agreement with run B and with the Beardsmore et al. (2016) map is still good along the eastern edge. The posterior entropy also decreases substantially due to an increase in the probability of granite structures at greater depths (beneath 3.5 km).
The weight given to the gravity sensor is thus an important factor determining the behavior of the inversion throughout half the modeled volume. With weakened gravity constraints, the two modes for the inferred rock density in layer 3 separate widely (see Fig. 3), though the algorithm is still able to move between the modes occasionally. The marginal distributions of the other rock properties do not change substantially and remain unimodal.
The comparison map for the inversion of Beardsmore et al. (2016) comes from the deterministic inversion of Meixner and Holgate (2009), which uses gravity as the main surface sensor but relies heavily on seismic data, with reflection horizons used to constrain the depth to basement and measurements of wave velocities (which correlate with density) from a P-wave refraction survey to constrain density at depth. While Meixner and Holgate (2009) mention constraints on rock densities, no mention is made of the level of agreement with the gravity data.
Without more information – a seismic sensor in our inversion, priors based on the specific seismic interpretations of Meixner and Holgate (2009), or specific knowledge about the noise level in the gravity dataset that would justify an informative prior – it is hard to say how concerned we should be about the differences between the deterministic inversion and our probabilistic version. The comparison certainly highlights the potential importance of seismic data, as a constraint on both rock properties at depth and on the geometry of geological structures.
Indeed, one potential weakness of this approach to balancing sensors is model inadequacy: the residuals from the inference may include systematic residuals from unresolved structure in the model, in addition to sensor noise. The presence of such residuals is a model selection question that in a traditional inversion context would be resolved by comparing residuals to the assumed noise level, but this depends strongly upon informative prior knowledge of the sensing process for all sensors used in the inversion. The remaining experiments will use the Cauchy likelihood unless otherwise specified.
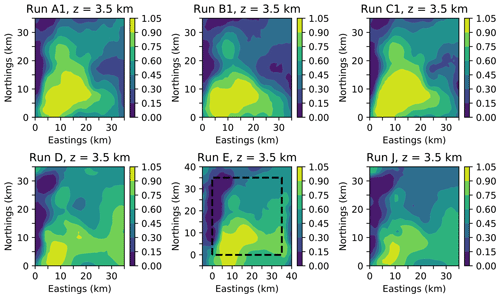
Figure 4Slices through the voxelized posterior probability of occupancy by granite for each run at a depth of 3.5 km.
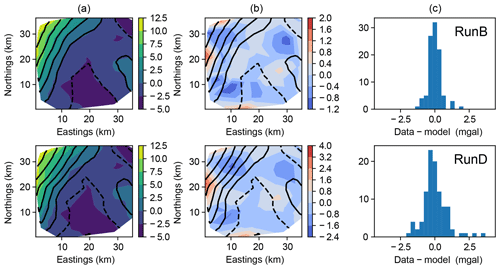
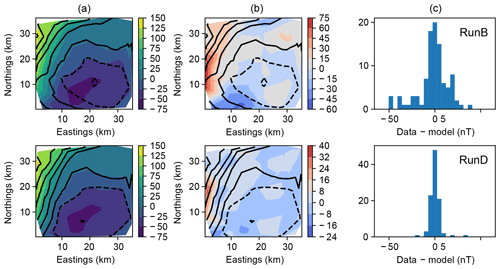
Figure 5Gravity anomaly at the surface (z=0). In a contour plot (a), filled contours are observations, and black lines represent mean posterior forward model prediction. Residuals of observations from the mean posterior forward model are also shown as a contour map (b) and histogram (c).
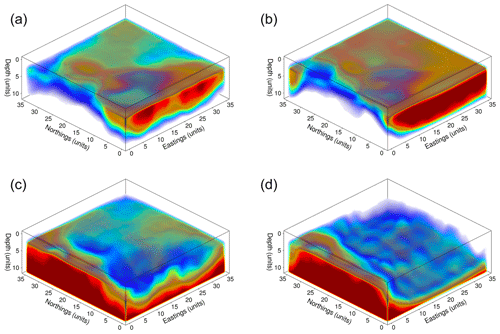
Figure 7Volume renderings of the posterior mean for runs B (a, c) and D (b, d), demonstrating the change in inference at depth. (a, b) Probability of occupancy for layer 5 (granite intrusion). (c, d) Probability of occupancy for layer 6 (basement). Red volumes indicate high probability, and blue volumes indicate low probability; zero-probability regions have been rendered transparent to make the shape of the region more readily visible.
3.3 Boundary conditions
The boundary conditions that Obsidian imposes on world voxelizations assume that rock properties rendered at a boundary edge (north–south, east–west) extend indefinitely off the edges, e.g.,
This may not be a good approximation when rock properties show strong gradients near the boundary. The residual plots in Figs. 5 and 6 show persistently high residuals along the western edge of the world, where such gradients appear in both the gravity anomaly and the magnetic anomaly.
For geophysical sensors with a localized response, one way to mitigate this is to include in the world representation a larger area than the sensor data cover, incorporating a margin with a width comparable to the scale of boundary artifacts, in order to let the model respond to edge effects for sensors with a finite area of response. In run E, we add a boundary zone of width 5 km around the margins of the world while increasing the number of control points in the granite intrusion layer boundary from 49 (7×7 grid) to 64 (8×8 grid). The model residuals and the inferred rock geometry do not differ substantially from the previous run, suggesting that the remaining outliers are actual outliers and not primarily due to mismatched boundary conditions. The autocorrelation time, however, increases substantially due to both the increase in the problem dimension and the fact that the new world parameters are relatively unconstrained and hence poorly scaled relative to the others.
3.4 Looser priors on rock properties and layer depths
In cases in which samples of rock for a given layer are few or unavailable, the empirical covariance used to build the prior on rock properties may be highly uncertain or undefined. In these cases, the user may have to resort to a broad prior on rock properties. The limiting case is when no petrophysical data are available at all. Similarly, definitive data on layer depths may become unavailable in the absence of drill cores, or at least seismic data, so a broad prior on control point depths may also become necessary.
We rerun the main Moomba analysis using two new priors. The first (run J) simulates the absence of petrophysical measurements. The layer depth priors are the same as the Beardsmore et al. (2016) setup, but the rock property prior for each layer is now replaced by an independent Gaussian prior on each rock property, with the same mean as in previous runs but a large width common to all layers:
The standard deviations are 0.2 g,cm−3 (density), 0.5 (log magnetic susceptibility), and 0.7 (log resistivity in Ωm).
The run J voxelization shows reasonable correspondence with the baseline run D, though with larger uncertainty, particularly in the northwest corner. In the absence of petrophysical samples but taking advantage of priors on overlying structure from seismic interpretations, a preliminary segmentation of granite from basement can thus still be obtained using broad priors on rock properties. Although the algorithm cannot reliably infer the bulk rock properties in the layers, the global prior on structure is enough for it to pick out the shapes of intrusions by looking for changes in bulk properties between layers.
The second run (run K) removes structural prior information instead of petrophysical prior information. The priors on rock properties are as in the Beardsmore et al. (2016) setup, but the control point prior for each layer is replaced by a multivariate Gaussian with the same anisotropic Gaussian covariance:
with σα=3 km.
Run K yields no reliable information about the location of granite at 3.5 km of depth. This seems to be solely due to the uncertain thickness of layers of sedimentary rock that are constrained to be nearly uniform horizontal slabs in run J, corresponding to a known insensitivity to depth among potential-field sensors. When relaxed, these strong priors cause a crisis of identifiability for the resulting models. Further variations on runs J and K show that replacing these multiple thin layers with a single uniform slab of ∼3 km depth (runs J2 and K2) does not aid convergence or accuracy, as long as more than one layer boundary is allowed to have large-scale structure.
As mentioned above and in Beardsmore et al. (2016), the strong priors on layer boundaries and locations were originally derived from seismic sensor data. Such data will not always be available but seem to be critical to constrain the geometry of existing layers to achieve a plausible inversion at depth.
Our experiments show concrete examples of how the efficiency of MCMC sampling changes with assumptions about the prior, likelihood, and proposal distributions for an Obsidian inversion, particularly as tight constraints on the solution are relaxed and uncertainty increases. Unrealistically tight constraints can hamper sampling, but relaxing priors or likelihoods may sometimes widen the separation between modes (as shown in Fig. 3), which also makes the posterior difficult to sample. Additionally, particular weaknesses in sensors, such as the insensitivity of potential-field sensors to the depth of geological features or to the addition of any horizontally invariant density distribution, can make it impossible to distinguish between multiple plausible alternatives, thus adding to the irregularity and multi-modality of the posterior.
While any single data source may be easy to understand on its own, unexpected interactions between parameters can also arise. Structural priors from seismic data or geological field measurements appear to play a crucial role in stabilizing the inversions in this paper, as seen by the collapse of our inversion after relaxing them.
Our findings reinforce the impression that to make Bayesian inversion techniques useful in this context, the computational burden must be reduced by developing efficient sampling methods. Three complementary ways forward present themselves:
-
developing MCMC proposals, or nonparametric methods to approximate probability distributions, that function in (relatively) high-dimensional spaces and capture local structure in the posterior;
-
developing fast approximate forward models for complex sensors (especially seismic) that deliver detailed information at depth, along with new ways of assessing and reducing model inadequacy; and
-
developing richer world parameterizations of 3-D geological models that faithfully represent real-world structure in as few dimensions as possible.
All three of the MCMC proposals studied here are variations of random walks, which explore parameter space by diffusion and do not easily handle posteriors with detailed local covariance structures such as the ones we find here. Proposals that can sense and adjust to local structure from the present state require, almost by definition, knowledge of the posterior's gradient (as in Hamiltonian Monte Carlo; Duane et al., 1987; Hoffman and Gelman, 2014; Neal, 2011) or higher-order curvature tensors (Girolami and Calderhead, 2011, as in Riemannian manifold Monte Carlo) with respect to the model parameters, which in turn require the gradients of both the prior and the likelihood (in particular of forward models).
Taking derivatives of a complex forward model by finite differences is also likely to be prohibitively expensive, and practitioners may not have the luxury of rewriting their forward model code to return derivatives. This is one goal of writing fast emulations of forward models, particularly emulations for which derivatives can be calculated analytically (see, for example, Fichtner et al., 2006a, b). Smooth universal approximators, such as artificial neural networks, are one possibility; Gaussian process latent variable models (Titsias and Lawrence, 2010) and Gaussian process regression networks (Wilson et al., 2012) are others, which would also enable nonlinear dimensionality reduction for difficult forward models or posteriors. Algorithms that alternate between fast and approximate forward models for local exploration, on the one hand, and expensive and precise forward models for evaluation of the objective function, on the other, have proved useful in engineering design problems (Jin, 2011; Sóbester et al., 2014). These approximate emulators give rise to model inadequacy terms in the likelihood, which can be explicitly addressed; for example, Köpke et al. (2018) present a geophysics inversion framework in which the inference scheme learns a model inadequacy term as sampling proceeds, showing proof of principle on a cross-hole georadar tomography inversion. A related, complementary route is to produce analytically differentiable approximations to the posterior that are built as the chain explores the space (Strathmann et al., 2015; Lan et al., 2016).
Another source of overall model inadequacy comes from the world parameterization, which can be viewed as part of the prior. Obsidian's world parameterization is tuned to match sedimentary basins and is thus best suited for applications such as oil, gas, and geothermal exploration; it is too limited to represent more complex structures, particularly those with folds and faults, that might arise in hard rock or mining scenarios. The GemPy package developed by de la Varga et al. (2019) makes an excellent start on a more general-purpose open-source code for 3-D geophysical inversions: it uses the implicit potential-field approach (Lajaunie et al., 1997) to describe geological structures, includes forward models for geophysical sensors, and is designed to produce posteriors that can easily be sampled by MCMC. GemPy is also specifically written to take advantage of autodifferentiation, providing ready derivative information for advanced MCMC proposals.
We have performed a suite of 3-D Bayesian geophysical inversions for the presence of granite at depth in the Moomba gas field of the Cooper Basin, including altering aspects of the problem setup to determine their effects on the efficiency and accuracy of MCMC sampling. Our main findings are as follows.
-
Parameterized worlds have much lower dimensionality than nonparametric worlds, and the parameters also offer a more interpretable description of the world – for example, boundaries between geological units are explicitly represented. However, the resulting posterior has a complex local covariance structure in parameter space, even for linear sensors.
-
Although isotropic random walk proposals explore such posteriors inefficiently, poorly adapted anisotropic random walks are even less efficient. A modified high-dimensional random walk such as pCN outperforms these proposals, and the prior-preserving properties of pCN make it especially attractive for use in tempered sampling.
-
The shape of the posterior and number of modes can also depend in complex ways upon the prior, making tempered proposals essential.
-
Hierarchical priors on observational noise provide a way to capture uncertainty about the weighting among datasets, although this may also make sampling more challenging, such as when priors on world parameters are relaxed.
-
Useful information about structures at depth can sometimes be obtained through sensor fusion even in the absence of informative priors. However, direct constraints on 3-D geometry from seismic interpretations or structural measurements seem to play a privileged role among priors owing to the relatively weak constraints on depth of structure afforded by potential-field methods.
In summary, both advanced MCMC methods and careful attention to the properties of the data are necessary for inversions to succeed.
The code for version 0.1.2 of Obsidian is available at https://doi.org/10.5281/zenodo.2580422 (Scalzo et al., 2019). All configuration files for 3-D model runs specified in this paper, together with corresponding datasets, are available in named subfolders of this repository and are also provided in the Supplement.
The usual mean square likelihood often used in geophysical sensor inversions assumes the residuals of the sensor measurements from each forward model are independent Gaussian-distributed with some variance σ2. In typical non-probabilistic inversions, this noise amplitude is specified exactly as part of the objective function. A probabilistic inversion would specify a prior P(σ2) for the probability density of the noise variance and condition the likelihood on this variance and on the other parameters describing the world.
Unless the noise levels in the sensors are themselves targets for inference, sampling will be more efficient if their values are integrated out beforehand. If the conditional likelihood is independent Gaussian, a point mass prior results in a Gaussian likelihood P(y|θ). If some uncertainty about σ2 exists, specifying the prior P(σ2) as an inverse gamma function enables the integration over σ2 to be done analytically. The parameter α describes the weight of the tail in the distribution of σ2, while β∕α gives a typical variance scale referring to the sample variance of the data; these parameters are then either specified by experts with prior knowledge about the sensors or are set to uninformative values, e.g., .
For a single observation y, we start with
where the mean μ is given by the forward model. Carrying out the integration over the prior proceeds as follows.
This is the density for a t distribution in the normalized residual with ν=2α degrees of freedom.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-12-2941-2019-supplement.
The study was conceptualized by SC, who with MG provided funding and resources. RS was responsible for project administration and designed the methodology under supervision from SC and GH. RS and DK carried out the development of the Obsidian code resulting in v0.1.2, carried out the main investigation and formal analysis, and validated and visualized the results. RS wrote the original draft text, for which all coauthors provided a review and critical evaluation.
The authors declare that they have no conflict of interest.
This work is part of the Lloyd's Register Foundation–Alan Turing Institute Programme for Data-Centric Engineering. Richard Scalzo thanks Lachlan McCalman, Simon O'Callaghan, and Alistair Reid for useful discussions about the development of Obsidian up to v0.1.1. The authors acknowledge the Sydney Informatics Hub and the University of Sydney’s high-performance computing cluster, Artemis, which have contributed to the results reported in this paper. This research was undertaken with the assistance of resources and services from the National Computational Infrastructure (NCI), which is supported by the Australian Government.
This paper was edited by Thomas Poulet and reviewed by two anonymous referees.
Agostinetti, N. P. and Malinverno, A.: Receiver function inversion by trans-dimensional Monte Carlo sampling, Geophys. J. Int., 181, 858–872, https://doi.org/10.1111/j.1365-246X.2010.04530.x, 2010. a, b, c
Anand, R. R. and Butt, C. R. M.: A guide for mineral exploration through the regolith in the Yilgarn Craton, Western Australia, Aust. J. Earth Sci., 57, 1015–1114, 2010. a
Beardsmore, G.: Data fusion and machine learning for geothermal target exploration and characterisation, Tech. rep., NICTA Final Report, available at: https://arena.gov.au/projects/data-fusion-and-machine-learning-for-geothermal/ (last access: 10 July 2019), 2014. a, b, c, d
Beardsmore, G., Durrant-Whyte, H., McCalman, L., O’Callaghan, S., and Reid, A.: A Bayesian inference tool for geophysical joint inversions, ASEG Extended Abstracts, 2016, 1–10, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Bodin, T., Sambridge, M., Tkalcic, H., Arroucau, P., Gallagher, K., and Rawlinson, N.: Transdimensional inversion of receiver functions and surface wave dispersion, Solid Earth, 117, B02301, https://doi.org/10.1029/2011JB008560, 2012. a, b, c
Calcagno, P., Chilès, J., Courrioux, G., and Guillen, A.: Geological modelling from field data and geological knowledge: Part I. Modelling method coupling 3D potential-field interpolation and geological rules, Phys. Earth Planet. Int., 171, 147–157, recent Advances in Computational Geodynamics: Theory, Numerics and Applications, 2008. a
Carr, L., Korsch, R. J., Reese, B., and Palu, T.: Onshore Basin Inventory: The McArthur, South Nicholson, Georgina, Wiso, Amadeus, Warburton, Cooper and Galilee basins, central Australia, Record 2016/04, Geoscience Australia, Canberra, 2016. a, b, c
Chandra, R., Azam, D., Müller, R. D., Salles, T., and Cripps, S.: BayesLands: A Bayesian inference approach for parameter uncertainty quantification in Badlands, Comput. Geosci., 131, 89–101, https://doi.org/10.1016/j.cageo.2019.06.012, 2019. a, b
Chib, S. and Greenberg, E.: Understanding the Metropolis-Hastings Algorithm, The American Statistician, 49, 327–335, 1995. a
Cotter, S. L., Roberts, G. O., Stuart, A. M., and White, D.: MCMC Methods for Functions: Modifying Old Algorithms to Make Them Faster, Stat. Sci., 28, 424–446, 2013. a, b
Cramer, H.: Mathematical methods of statistics, Princeton University Press, 1946. a
de la Varga, M. and Wellmann, J. F.: Structural geologic modeling as an inference problem: A Bayesian perspective, Interpretation, 4, SM1–SM16, 2016. a
de la Varga, M., Schaaf, A., and Wellmann, F.: GemPy 1.0: open-source stochastic geological modeling and inversion, Geosci. Model Dev., 12, 1–32, https://doi.org/10.5194/gmd-12-1-2019, 2019. a, b, c
Duane, S., Kennedy, A. D., Pendleton, B. J., and Roweth, D.: Hybrid Monte Carlo, Phys. Lett. B, 195, 216–222, 1987. a
Fichtner, A., Bunge, H.-P., and Igel, H.: The adjoint method in seismology: I. Theory, Phys. Earth Planet. Int., 157, 86–104, 2006a. a
Fichtner, A., Bunge, H.-P., and Igel, H.: “The adjoint method in seismology: II. Applications: travel times and sensitivity functionals”, Phys. Earth Planet. Int., 157, 105–123, 2006b. a
Gelman, A. and Rubin, D.: Inference from Iterative Simulation Using Multiple Sequences, Stat. Sci., 7, 457–472, 1992. a
Geyer, C. J. and Thompson, E. A.: Annealing Markov Chain Monte Carlo with Applications to Ancestral Inference, J. Am. Stat. Assoc., 90, 909–920, 1995. a
Giraud, J., Jessell, M., Lindsay, M., Martin, R., Pakyuz-Charrier, E., and Ogarko, V.: Uncertainty reduction of gravity and magnetic inversion through the integration of petrophysical constraints and geological data, in: EGU General Assembly Conference Abstracts, Vol. 18, EPSC2016–3870, 2016. a, b
Giraud, J., Pakyuz-Charrier, E., Jessell, M., Lindsay, M., Martin, R., and Ogarko, V.: Uncertainty reduction through geologically conditioned petrophysical constraints in joint inversion, Geophysics, 82, ID19–ID34, 2017. a, b
Giraud, J., Pakyuz-Charrier, E., Ogarko, V., Jessell, M., Lindsay, M., and Martin, R.: Impact of uncertain geology in constrained geophysical inversion, ASEG Extended Abstracts, 2018, 1, 2018. a
Girolami, M. and Calderhead, B.: Riemann manifold langevin and hamiltonian monte carlo methods, J. Roy. Stat. Soc. Ser. B (Statistical Methodology), 73, 123–214, 2011. a, b
Goodman, J. and Weare, J.: Ensemble samplers with affine invariance, Commun. Appl. Mathe. Comput. Sci., 5, 65–80, 2010. a
Green, P. J., Łatuszyński, K., Pereyra, M., and Robert, C. P.: Bayesian computation: a perspective on the current state, and sampling backwards and forwards, Stat. Comput., 25, arXiv:1502.01148, 2015. a
Gupta, V. K. and Grant, F. S.: 30. Mineral-Exploration Aspects of Gravity and Aeromagnetic Surveys in the Sudbury-Cobalt Area, Ontario, 392–412, Society of Exploration Geophysicists, 1985. a
Haario, H., Saksman, E., and Tamminen, J.: An Adaptive Metropolis Algorithm, Bernoulli, 7, 223–242, 2001. a, b
Hastings, W. K.: Monte Carlo sampling methods using Markov chains and their applications, Biometrika, 57, 97–109, 1970. a
Hoffman, M. D. and Gelman, A.: The No-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo, J. Mach. Learn. Res., 15, 1593–1623, 2014. a
Jessell, M.: Three-dimensional geological modelling of potential-field data, Comput. Geosci., 27, 455–465, 3D reconstruction, modelling & visualization of geological materials, 2001. a
Jin, Y.: Surrogate-assisted evolutionary computation: Recent advances and future challenges, Swarm Evol. Comput., 1, 61–70, 2011. a
Köpke, C., Irving, J., and Elsheikh, A. H.: Accounting for model error in Bayesian solutions to hydrogeophysical inverse problems using a local basis approach, Adv. Water Resour., 116, 195–207, 2018. a
Lajaunie, C., Courrioux, G., and Manuel, L.: Foliation fields and 3D cartography in geology: Principles of a method based on potential interpolation, Math. Geol., 29, 571–584, https://doi.org/10.1007/BF02775087, 1997. a, b
Laloy, E., Linde, N., Jacques, D., and Mariethoz, G.: Merging parallel tempering with sequential geostatistical resampling for improved posterior exploration of high-dimensional subsurface categorical fields, Adv. Water Resour., 90, 57–69, 2016. a, b, c, d
Lan, S., Bui-Thanh, T., Christie, M., and Girolami, M.: Emulation of higher-order tensors in manifold Monte Carlo methods for Bayesian Inverse Problems, J. Comput. Phys., 308, 81–101, 2016. a
Lindsay, M., Jessell, M., Ailleres, L., Perrouty, S., de Kemp, E., and Betts, P.: Geodiversity: Exploration of 3D geological model space, Tectonophysics, 594, 27–37, 2013. a
MacCarthy, J. K., Borchers, B., and Aster, R. C.: Efficient stochastic estimation of the model resolution matrix diagonal and generalized cross–validation for large geophysical inverse problems, J. Geophys. Res., 116, B10304, https://doi.org/10.1029/2011JB008234, 2011. a
McCalman, L., O'Callaghan, S. T., Reid, A., Shen, D., Carter, S., Krieger, L., Beardsmore, G. R., Bonilla, E. V., and Ramos, F. T.: Distributed bayesian geophysical inversions, Proceedings of the Thirty-Ninth Workshop on Geothermal Reservoir Engineering, Stanford University, 1–11, 2014. a, b, c, d, e, f, g
Meixner, T. and Holgate, F.: The Cooper Basin Region 3D Geological Map Version 1: A search for hot buried granites, Geoscience Australia, Record 2009/15, 2009. a, b, c, d
Menke, W.: Geophysical Data Analysis (Revised Edition), Elsevier Ltd, 2018. a
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E.: Equation of state calculations by fast computing machines, J. Chem. Phys., 21, 1087–1092, 1953. a
Miasojedow, B., Moulines, E., and Vihola, M.: An adaptive parallel tempering algorithm, J. Comput. Graph. Stat., 22, 649–664, 2013. a
Mockus, J.: Bayesian approach to global optimization: theory and applications, Kluwer Academic Press, 2013. a
Mosegaard, K. and Tarantola, A.: Monte Carlo sampling of solutions to inverse problems, J. Geophys. Res.-Solid Earth, 100, 12431–12447, 1995. a, b, c
Nabighian, M. N., Ander, M. E., Grauch, V. J. S., Hansen, R. O., LaFehr, T. R., Li, Y., Pearson, W. C., Peirce, J. W., Phillips, J. D., and Ruder, M. E.: Historical development of the gravity method in exploration, Geophysics, 70, 63ND–89ND, 2005a. a
Nabighian, M. N., Grauch, V. J. S., Hansen, R. O., LaFehr, T. R., Li, Y., Peirce, J. W., Phillips, J. D., and Ruder, M. E.: The historical development of the magnetic method in exploration, Geophysics, 70, 33ND–61ND, 2005b. a
Neal, R. M.: MCMC using Hamiltonian dynamics, Handbook of Markov Chain Monte Carlo, 2, 2011. a, b
Olierook, H. K. H., Timms, N. E., Wellmann, J. F., Corbel, S., and Wilkes, P. G.: 3D structural and stratigraphic model of the Perth Basin, Western Australia: Implications for sub-basin evolution, Aust. J. Earth Sci., 62, 447–467, 2015. a
Pakyuz-Charrier, E., Giraud, J., Ogarko, V., Lindsay, M., and Jessell, M.: Drillhole uncertainty propagation for three-dimensional geological modeling using Monte Carlo, Tectonophysics, 747-748, 16–39, https://doi.org/10.1016/j.tecto.2018.09.005, 2018a. a, b
Pakyuz-Charrier, E., Lindsay, M., Ogarko, V., Giraud, J., and Jessell, M.: Monte Carlo simulation for uncertainty estimation on structural data in implicit 3-D geological modeling, a guide for disturbance distribution selection and parameterization, Solid Earth, 9, 385–402, 2018b. a, b
Pall, J., Chandra, R., Azam, D., Salles, T., Webster, J., and Cripps, S.: BayesReef: A Bayesian inference framework for modelling reef growth in response to environmental change and biological dynamics, arXiv preprint arXiv:arXiv:tba, 2018. a
Rao, C. R.: Information and the accuracy attainable in the estimation of statistical parameters, B. Cal. Math. Soc., 37, 81–89, 1945. a
Roberts, G. O. and Rosenthal, J. S.: Coupling and ergodicity of adaptive Markov chain Monte Carlo algorithms, J. Appl. Prob., 44, 458–475, 2007. a
Roberts, G. O., Gelman, A., Gilks, W. R., et al.: Weak convergence and optimal scaling of random walk Metropolis algorithms, Ann. Appl. Prob., 7, 110–120, 1997. a
Ruggeri, P., Irving, J., and Holliger, K.: Systematic evaluation of sequential geostatistical resampling within MCMC for posterior sampling of near-surface geophysical inverse problems, Geophys. J. Int., 202, 961–975, 2015. a, b, c
Sabins, F. F.: Remote sensing for mineral exploration, Ore Geol. Rev., 14, 157–183, 1999. a
Salama, W., Anand, R. R., and Verrall, M.: Mineral exploration and basement mapping in areas of deep transported cover using indicator heavy minerals and paleoredox fronts, Yilgarn Craton, Western Australia, Ore Geol. Rev., 72, 485–509, 2016. a
Sambridge, M.: Exploring multidimensional landscapes without a map, Inverse Problems, 14, 427–440, https://doi.org/10.1088/0266-5611/14/3/005, 1998. a
Sambridge, M. and Mosegaard, K.: Monte Carlo methods in geophysical inverse problems, Rev. Geophys., 40, 1–29, 2002. a, b, c
Sambridge, M., Bodin, T., Gallagher, K., and Tkalcic, H.: Transdimensional inference in the geosciences, Philo. Trans. Roy. Soc. A:, 371, 20110547–20110547, iSBN 1364503X (ISSN), 2012. a, b, c
Scalzo, R., Kohn, D., OĆallaghan, S., McCalman, L., and Simpson-Young, B.: rscalzo/obsidian: 0.1.2-beta, https://doi.org/10.5281/zenodo.2580422, 2019. a, b, c
Shannon, C. E.: A mathematical theory of communication, Bell Syst. Tech. J., 27, 379–423, 1948. a
Silva, J. B. C. and Cutrim, A.: A robust maximum likelihood method for gravity and magnetic interpretation, Geoexploration, 26, 1-–31, 1989. a
Sóbester, A., Forrester, A. I. J., Toal, D. J. J., Tresidder, E., and Tucker, S.: Engineering design applications of surrogate-assisted optimization techniques, Opt. Eng., 15, 243–265, 2014. a
Strangway, D. W., C. M. Swift, J., and Holmer, R. C.: The application of audio-frequency magnetotellurics (AMT) to mineral exploration, Geophysics, 38, 1159–1175, 1973. a
Strathmann, H., Sejdinovic, D., Livingstone, S., Szabo, Z., and Gretton, A.: Gradient-free Hamiltonian Monte Carlo with efficient kernel exponential families, in: Advances in Neural Information Processing Systems, 955–963, 2015. a, b
Tarantola, A.: Inverse problem theory and methods for model parameter estimation, Vol. 89, siam, 2005. a
Tarantola, A. and Valette, B.: Generalized nonlinear inverse problems solved using the least squares criterion, Rev. Geophys., 20, 219–232, 1982. a, b
Titsias, M. and Lawrence, N.: Bayesian Gaussian Process Latent Variable Model, Artificial Intelligence, 9, 844–851, arXiv: 1309.6835, ISBN 978-1-4503-1285-1, 2010. a
Wellmann, J. F. and Regenauer-Lieb, K.: Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models, Tectonophysics, 526, 207–216, 2012. a, b
Wellmann, J. F., Horowitz, F. G., Schill, E., and Regenauer-Lieb, K.: Towards incorporating uncertainty of structural data in 3D geological inversion, Tectonophysics, 490, 141–151, 2010. a, b
Wilson, A. G., Knowles, D. A., and Ghahramani, Z.: Gaussian Process Regression Networks, International Conference on Machine Learning, p. 17, arXiv: 1110.4411, 2012. a
Wrona, T., Pan, I., Gawthorpe, R. L., and Fossen, H.: Seismic facies analysis using machine learning, Geophysics, 83, O83–O95, 2018. a
Xiang, E., Guo, S. E., Liu, J., Dong, H., and Ren, Z.: Efficient hierarchical transdimensional Bayesian inversion of magnetotelluric data, Geophys. J. Int., 37, 81–89, 2018. a, b, c