the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Overview of the PALM model system 6.0
Björn Maronga
Sabine Banzhaf
Cornelia Burmeister
Thomas Esch
Renate Forkel
Dominik Fröhlich
Vladimir Fuka
Katrin Frieda Gehrke
Jan Geletič
Sebastian Giersch
Tobias Gronemeier
Günter Groß
Wieke Heldens
Antti Hellsten
Fabian Hoffmann
Atsushi Inagaki
Eckhard Kadasch
Farah Kanani-Sühring
Klaus Ketelsen
Basit Ali Khan
Christoph Knigge
Helge Knoop
Pavel Krč
Mona Kurppa
Halim Maamari
Andreas Matzarakis
Matthias Mauder
Matthias Pallasch
Dirk Pavlik
Jens Pfafferott
Jaroslav Resler
Sascha Rissmann
Emmanuele Russo
Mohamed Salim
Michael Schrempf
Johannes Schwenkel
Gunther Seckmeyer
Sebastian Schubert
Matthias Sühring
Robert von Tils
Lukas Vollmer
Simon Ward
Björn Witha
Hauke Wurps
Julian Zeidler
Siegfried Raasch
In this paper, we describe the PALM model system 6.0. PALM (formerly an abbreviation for Parallelized Large-eddy Simulation Model and now an independent name) is a Fortran-based code and has been applied for studying a variety of atmospheric and oceanic boundary layers for about 20 years. The model is optimized for use on massively parallel computer architectures. This is a follow-up paper to the PALM 4.0 model description in Maronga et al. (2015). During the last years, PALM has been significantly improved and now offers a variety of new components. In particular, much effort was made to enhance the model with components needed for applications in urban environments, like fully interactive land surface and radiation schemes, chemistry, and an indoor model. This paper serves as an overview paper of the PALM 6.0 model system and we describe its current model core. The individual components for urban applications, case studies, validation runs, and issues with suitable input data are presented and discussed in a series of companion papers in this special issue.
- Article
(9003 KB) - Full-text XML
- BibTeX
- EndNote
Since the early 1970s, the turbulence-resolving so-called large-eddy simulation (LES) technique has been increasingly employed for studying the atmospheric boundary layer (ABL) at large Reynolds numbers. While the earliest studies were performed at coarse grid spacings on the order of 100 m (Deardorff, 1970, 1973), today's supercomputers allow for large domain runs at fine grid spacings of 1–10 m (e.g., Kanda et al., 2004; Raasch and Franke, 2011; Sullivan and Patton, 2011, among many others) or even less (Sullivan et al., 2016; Maronga and Reuder, 2017; Maronga and Bosveld, 2017). LES models solve the three-dimensional prognostic equations for momentum, temperature, humidity, and other scalar quantities (such a chemical species). The principle of LES dictates a separation of scales. Turbulence scales larger than a chosen filter width are being directly resolved by LES models, while the effect of smaller turbulence scales on the resolved scales is fully parameterized within a so-called subgrid-scale (SGS) model. The filter width strongly depends on the phenomenon to be studied and must be chosen in such a way that at least 90 % of the turbulence energy can be resolved (Heus et al., 2010).
In a precursor paper (Maronga et al., 2015), we gave an overview of the Parallelized Large-eddy Simulation Model (PALM) version 4.0. PALM is a Fortran-based code and has been applied for a variety of atmospheric and oceanic boundary layers for about 20 years. The model is optimized for use on massively parallel computer architectures but can be used in principle also on small workstations and notebooks. The model domain is discretized in space using finite differences and equidistant horizontal grid spacings. The parallelization of the code is achieved by a 2-D domain decomposition method along the x and y directions on a Cartesian grid with (usually) equally sized subdomains. Ghost layers are added at the side boundaries of the subdomains in order to account for the local data dependencies, which are caused by the need to compute finite differences at these positions. A Cartesian topography (complex terrain and buildings) is available in PALM, which is based on the mask method (Briscolini and Santangelo, 1989) and allows for explicitly resolving solid obstacles such as buildings and orography. PALM also has an ocean option, allowing for studying the ocean mixed layer where the sea surface is defined at the top of the model, and which includes a prognostic equation for salinity.
Furthermore, PALM has offered several embedded models which were described in the precursor paper, namely bulk cloud microphysics parameterizations, a Lagrangian particle model (LPM) which can be used for studying dispersion processes in turbulent flows, or as a Lagrangian cloud model (LCM) employing the superdroplet approach. Moreover, a plant canopy model can be used to study effects of plants as obstacles on the flow. A 1-D version of PALM can be switched on in order to generate steady-state wind profiles for 3-D model initialization.
Due to the enormous amount of data that come along with computationally expensive LES (in terms of the number of grid points and short time steps), the data handling plays a key role for the performance of LES models and for data analysis during post-processing. PALM is optimized to pursue the strategy of performing data operations like time or domain averaging to a great extent online instead of postpone such operations to a post-processing step. In this way, the data output (e.g., of huge 4-D data or temporal averages) can be significantly reduced. In order to allow the user to perform their own calculations during runtime, a user interface offers a wide range of possibilities, e.g., for defining user-defined output quantities. PALM allows data output for different quantities as time series, (horizontally averaged) vertical profiles, 2-D cross sections, 3-D volume data, and masked data. All data output files are in netCDF format, which can be processed by a variety of public domain and commercial software. The only exception is data output from the LPM, which is output in Fortran binary format for a better performance. For details about PALM's specifics, application scenarios, and validation runs, see Maronga et al. (2015) and references therein.
In the present paper, we describe the PALM model system version 6.0. Since version 4.0, the code has undergone massive changes and improvements. Above all, new components for applications of PALM in urban environments, so-called PALM-4U (PALM for urban applications) components, have been added in the scope of the Urban Climate Under Change [UC]2 framework funded by the German Federal Ministry of Education and Research (Scherer et al., 2019b; Maronga et al., 2019). Besides, a turbulence closure based on the Reynolds-averaged Navier–Stokes (RANS) equations was added, enabling PALM to not only run in turbulence-resolving (i.e., LES) but also in RANS mode where the full turbulence spectrum is parameterized. Originally, the name PALM referred to its parallelization as a special feature of the model. Nowadays, however, most of the existing LES models are parallelized.
Moreover, with the RANS mode implemented, PALM is more than an LES model, rendering the full name of the model inappropriate. As the name PALM has been established in the research community, we thus decided to drop the full name and use the abbreviation PALM as a proper name from now on. The model is now referred to as the PALM model system, consisting of the PALM model core and the PALM-4U components. For the motivation for developing the PALM-4U components and a description of model developments done within [UC]2, the reader is referred to Maronga et al. (2019). As the model core in version 4.0 was described in detail in the precursor paper, we will focus here on the changes in the model core and give an overview of all the new components that have been added to the model. The individual new PALM-4U components, case studies, validation studies, and issues with suitable input data are presented and discussed in a series of companion papers in this special issue.
The paper is organized as follows: Sect. 2 deals with the description of the model core, while Sect. 3 and Sect. 4 give details about the embedded modules in the PALM core and the PALM-4U components, respectively. Sect. 5 provides technical details, including recent developments in model operation, data structure of surface elements, I/O data handling, and optimization. The paper closes with conclusions in Sect. 6. Note that all symbols that will be introduced in the following are also listed in Tables 1–8.
In this section, we give a detailed description of the changes of the PALM model core starting from version 4.0. Here, we confine ourselves to the atmospheric version. Details about the ocean version are given by Maronga et al. (2015) and in Sect. 2.4. By default, PALM solves equations for up to seven prognostic variables: the velocity components u, v, and w on a staggered Cartesian grid (staggered Arakawa C grid Harlow and Welch, 1965; Arakawa and Lamb, 1977), potential temperature θ, SGS turbulence kinetic energy (SGS-TKE) e (in LES mode), water vapor mixing ratio qv, and possibly a passive scalar s. Note that, in PALM 4.0, it was only possible to use either water vapor or the passive scalar as both used the same prognostic equation in the model code, while both are now fully separated and can be used simultaneously.
2.1 Governing equations of the PALM core
By default, PALM solves incompressible approximations of the Navier–Stokes equations, either in Boussinesq-approximated form, filtered based on a spatial scale separation approach after Schumann (1975) (described in Maronga et al., 2015), or in an anelastic approximation, in which the flow is treated as incompressible but allowing for density variations with height, while variations in time are not permitted. This enables the application of PALM to simulate atmospheric phenomena that extend throughout the entire troposphere (e.g., deep convection). Both anelastic and Boussinesq-approximated forms are described by a single set of equations that only differ in the treatment of the density ρ. For the Boussinesq form, ρ is set to a constant value (and then drops out of most terms), while the anelastic form results from varying ρ with height during initialization.
In the following set of equations, angular brackets denote a horizontal domain average. A subscript 0 indicates a surface value. Note that the variables in the equations are implicitly filtered by the discretization (see above), but that the continuous form of the equations is used here for convenience. A double prime indicates SGS variables. The overbar indicates filtered quantities. The equations for the conservation of mass, momentum, thermal internal energy, moisture, and another arbitrary passive scalar quantity, filtered over a grid volume on a Cartesian grid, then read as
Here, . ui is the velocity components () with location xi (), t is time, is the Coriolis parameter with being the Earth's angular velocity and ϕ being the geographical latitude. ug,j is the geostrophic wind speed components, ρ is the basic state density of dry air, is the modified perturbation pressure with p∗ being the perturbation pressure and , is the gravitational acceleration, δ is the Kronecker delta, and is the specific latent heat of vaporization. The reference state θv,ref in Eq. (2) can be set to be the horizontal average 〈θv〉, the initial state, or a fixed reference value. Furthermore, and χs are source/sink terms of qv and s, respectively. The potential temperature is defined as
with the absolute temperature T and the Exner function:
with p being the hydrostatic air pressure, p0=1000 hPa a reference pressure, Rd=287 the specific gas constant for dry air, and cp=1005 the specific heat of dry air at constant pressure. The virtual potential temperature is defined as
with the specific gas constant for water vapor , and the liquid water mixing ratio ql. For the computation of ql, see the descriptions of the embedded cloud microphysical models in Sect. 3.1 and 3.4.
2.2 Turbulence closures
By default, PALM employs a 1.5-order closure (LES mode) after Deardorff (1980) in the formulation by Moeng and Wyngaard (1988) and Saiki et al. (2000) (hereafter referred to as the Deardorff scheme). Details are given in Maronga et al. (2015). Since version 6.0, an alternative dynamic SGS closure can be used, which will be described in the following. Moreover, two turbulence closures are available in RANS mode (i.e., the full spectrum of turbulence is parameterized): a so-called TKE-l and a TKE-ϵ closure, where l is a mixing length and ϵ is the SGS-TKE dissipation rate.
Blackadar (1962)2.2.1 Dynamic SGS closure
The dynamic SGS closure follows Heinz (2008) and Mokhtarpoor and Heinz (2017). In general, the dynamic SGS closure employs the same equations for calculating the SGS fluxes as the Deardorff scheme, assuming that the energy transport by SGS eddies is proportional to the local gradients of the mean resolved quantities and reads
where Km and Kh are the local SGS diffusivities of momentum and heat, respectively. In order to distinguish between different filter operations, the overbar is used to denote variables that are filtered with the horizontal grid spacing Δ in this subsection. While Kh is calculated as in the Deardorff scheme, a dynamic approach is applied to calculate Km, viz.
where . Unlike in the Deardorff scheme, c∗ is not a fixed value but is calculated at each time step for each grid cell. As for the Deardorff scheme, e is calculated using a prognostic equation:
with l being a mixing length. Note that, in the SGS closures, θv,ref refers to either a given reference value or the local value of . The pressure term in Eq. (14) is parameterized as
The left-hand side of Eq. (9) is called deviatoric subgrid stress. Using the rate of strain tensor , it can be written as follows:
where we used the summation convention. The subgrid stress can also be expressed as . This expression makes clear why the subgrid stress has to be modeled, since only the second term of the right-hand side is known. Following Germano et al. (1991), a test filter is introduced, which is ΔT=2Δ in our case. The subgrid stress on the test filter scale then is , where also the first term on the right-hand side is unknown (the hat denotes a filter operation with the width of the test filter). The difference between subgrid stress on the test filter level and the test-filtered subgrid stress is the resolved stress . Both terms on the right-hand side are known, and Lij can thus be calculated directly by application of the test filter to the resolved velocities on the grid cells. As described in Heinz (2008), c∗ can be calculated via
where is the subtest-scale viscosity. The stability of the simulation is ensured by using dynamic bounds that keep the values of c∗ in the range
as derived by Mokhtarpoor and Heinz (2017). This model does not need artificial limitation of the range of c∗ for stable runs and allows the occurrence of energy backscatter (i.e., negative values of Km). Unlike other dynamic models, this formulation of c∗ is not derived using model assumptions for the subgrid stress and the stress on the test filter level but is derived as consequence of stochastic analysis (Heinz, 2008; Heinz and Gopalan, 2012).
2.2.2 RANS turbulence closures
For RANS mode, PALM offers two different turbulence closures – a TKE-l and the standard TKE-ϵ closure (Mellor and Yamada, 1974, 1982) – to calculate the eddy diffusivities, which then describe diffusion by the complete turbulence spectrum. While the TKE-l closure uses a single prognostic equation to calculate the TKE, the standard TKE-ϵ closure applies an additional prognostic equation for ϵ in addition to the equation for e.
In the TKE-l closure (e.g., Holt and Raman, 1988), the eddy diffusivities are calculated via e and l as
where Pr=1 denotes the Prandtl number and c0=0.55 denotes a model constant. The Prandtl number can be changed to a user-specific value for different stability regimes. Note that, in the case of RANS mode, e denotes the total turbulent kinetic energy as the full turbulence spectrum is parameterized. To calculate e, Eq. (14) is modified by introducing gradient approaches for the turbulent transport terms:
Here, is the diffusivity of e, with the model constant σe=1 as default value, and ϵ is calculated as
The mixing length l is calculated using the mixing length after Blackadar (1962) lB and the similarity function of momentum Φm for stable conditions in the formulation of Businger–Dyer (see, e.g., Panofsky and Dutton, 1984):
with
where κ=0.4 denotes the von Kármán constant, L the Obukhov length, and z the height above the surface. The mixing length is limited by lwall, which is the distance to the nearest solid surface.
Aside from the TKE-l closure, also a standard TKE-ϵ model is available as a turbulence closure. When choosing the standard TKE-ϵ model, Km is calculated via
The modeled TKE is calculated using Eq. (21) and an additional prognostic equation is used to calculate ϵ:
where with σϵ=1.3 and c1=1.44, c2=1.92, and c3=1.44 being model constants (e.g., Launder and Spalding, 1974; Oliveira and Younis, 2000). As the constants c0−c3 as well as σe and σϵ depend on the situation studied, they might need to be adjusted by the user.
2.3 Boundary conditions
2.3.1 Constant flux layer
Following Monin–Obukhov similarity theory (MOST), a constant flux layer assumption is used between the surface and the first computational grid level (k=1, ). Using roughness lengths for heat, humidity, and momentum (z0,h, z0,q, and z0, respectively), MOST then provides surface fluxes of momentum (shear stress) and scalar quantities (heat and moisture flux) as bottom boundary conditions. In PALM, it is assumed that MOST can be applied locally, even though there is no theoretical foundation for this assumption. Hultmark et al. (2013), e.g., pointed out that this leads to a systematical overprediction of the mean shear stress. However, this local method has the advantage that surface heterogeneities can be prescribed at the surface, and therefore it has become standard in most contemporary LES codes.
The surface layer vertical profile of the horizontal wind velocity is predicted by MOST through
where Φm is the similarity function for momentum in the formulation of Businger–Dyer (see, e.g., Panofsky and Dutton, 1984):
The scaling parameters θ∗ and q∗ are defined by MOST as
with the friction velocity u∗ (defined through the square root of the surface shear stress) as
In PALM, u∗ is calculated from uh at zmo by vertical integration of Eq. (28) over z from z0 to zmo.
From Eqs. (28), (31), and a geometric decomposition of both the wind vector and u*, it is possible to derive a formulation for the horizontal wind components, viz.
Vertical integration of Eq. (32) over z from z0 to zmo then yields the surface momentum fluxes and .
The formulations above all require knowledge of the scaling parameters θ∗ and q∗. These are deduced from vertical integration of
over z from z0,h to zmo. The similarity function Φh is given by
Previously, the implementation of the constant flux layer involved a diagnostic–prognostic equation for L, based on data from the previous time step. Even though it was found that this method introduces only negligible errors, we decided to revise this procedure and calculate L based on using a Newton iteration method instead. By doing so, we can achieve a correct value of L which can be important when the model is coupled to a surface scheme. We also found that this does not increase the computational costs to a significant amount (usually less than 1 %). Starting from PALM 6.0 (revision 3668), Newton iteration is the only available method. The Newton iteration method involves the calculation of a bulk Richardson number Rib. Depending on whether fluxes are prescribed or Dirichlet boundary conditions are used for temperature and humidity, Rib is related to L via
where
and
are the integrated universal profile stability functions of Ψm and Ψh (see Paulson, 1970; Holtslag and De Bruin, 1988), so that a (bulk) Richardson number can be defined:
The above equations are solved for L by finding the root of the function fN:
The solution is then given by iteration of
with iteration step n, and
until L meets a convergence criterion.
The surface fluxes of sensible and latent heat, as well as the surface shear stress, are then calculated using Eqs. (30) and (31). Note that for vertically oriented surfaces in combination with an interactive surface model switched on (see Sects. 3.5 and 4.5), the surface fluxes are calculated after Krayenhoff and Voogt (2007) as static stability considerations do not apply for such surface orientations (see also Resler et al., 2017). Also note that the above formulation can lead to violations of MOST for too-coarse grid spacings in some cases, particularly for setups of stable boundary layers, as the first grid layer might be located in the roughness sublayer of the surface layer. For a discussion of this issue and an improved boundary condition, see Basu and Lacser (2017) and Maronga et al. (2020).
In the case of the TKE-ϵ RANS closure, the boundary condition for e, ϵ, and Km are
2.3.2 Wave-dependent surface roughness
As the ocean surface in PALM is assumed to be flat and waves are not explicitly resolved, a Charnock parameterization can be switched on which relates the surface roughness lengths to the friction velocity as described in Beljaars (1994). This accounts for the fact that water surfaces become aerodynamically smooth for low wind speeds. For ocean surfaces, the roughness lengths are thus calculated for each surface grid point as
with αCh=0.0018 being the Charnock constant, and being the kinematic viscosity. Note that this parameterization is designed for large-scale models where waves are a subgrid-scale phenomenon. For fine grid spacings and/or large waves (in amplitude and wavelength), this parameterization can lead to erroneous roughness lengths and should not be switched on without rigorous testing.
2.3.3 Lateral boundary conditions
At lateral domain boundaries, various different conditions can be applied, which are listed in Table 9.
By default, cyclic boundary conditions apply at all lateral domain boundaries. Choosing an inflow boundary condition at one of the four domain boundaries requires to set an outflow condition at the opposing boundary while keeping the boundaries in perpendicular direction cyclic. An exception is made in the case of model nesting, where inflow/outflow boundary conditions are set dynamically for each individual boundary grid point (see Sect. 4.8 and 4.9).
The simplest inflow condition is a purely laminar inflow using Dirichlet conditions at either domain boundary. A more sophisticated approach with fully developed turbulence already present at the inflow boundary can be achieved by using the turbulence-recycling method, which is implemented according to Lund et al. (1998) and Kataoka and Mizuno (2002). The turbulence-recycling method sets a fixed mean inflow condition at one side of the simulation domain and adds a turbulent signal from within the model domain to these mean profiles. This then creates a turbulent inflow (see Maronga et al., 2015). The turbulence-recycling method is currently only available at the left domain boundary, i.e., at x=0.
The downside of the turbulence-recycling method is the requirement of an additional recycling area within the model domain which is purely needed to generate turbulence and cannot be used for data evaluation of the studied phenomenon. To avoid the necessity of including an additional recycling area within the simulation domain, a synthetic turbulence generator can be used instead of the turbulence-recycling method at the inflow boundary (Gronemeier et al., 2015). This turbulence generator is based on the method published by Xie and Castro (2008) with the modification of Kim et al. (2013) for divergence-free inflow. The turbulence-generation method calculates stochastic fluctuations from an arrayed random number. This is realized via given length scales that are added to the mean inflow profiles using a Lund rotation (Lund et al., 1998) and a given Reynolds stress tensor. In order to apply the synthetic turbulence generator, information on the turbulent length scales for the three wind components in the x, y, and z directions, as well as the Reynolds stress tensor, is required. These information can be either obtained from idealized precursor simulations or from observations (Xie and Castro, 2008). In combination with the offline nesting (see Sect. 4.9), PALM also offers the possibility to compute turbulent length scales and Reynolds stress following the parameterizations described by Rotach et al. (1996).
At the outflow boundary, radiation conditions are used by default for the velocity components as proposed by Orlanski (1976). Velocity components are advected by a transport velocity utr which is calculated from the gradients of the transported velocity components normal to the boundary at the grid points next to the outflow boundary (see also Maronga et al., 2015). The transport velocity is restricted to , where Δt denotes the time step.
In cases with weak background wind in a convective boundary layer, it was found that using the radiation condition can lead to instabilities and strong self-intensifying inflow regimes at the outflow boundary (Gronemeier et al., 2017). In order to prevent such artificial inflow situations at the outflow boundary, an empirical approach can be used at the outflow boundary, the so-called turbulent outflow condition (Gronemeier et al., 2017). Instead of transporting the velocity components via the radiation condition, instantaneous values of , , , , and e are taken from a vertical plane situated at a distance xd from the outflow boundary which are then mapped to the outflow boundary. By taking the information of the flow field from within the domain, occurring inflow regimes are disturbed and cannot intensify themselves as long as a proper xd is chosen which needs to be a fair distance away from the outflow boundary. Note that the turbulent outflow condition can be transformed into the radiation condition, where if xd=0. As for now, the turbulent outflow condition is only available at the right domain boundary.
2.4 Ocean option
PALM's ocean option has been extended to include wave effects to account for the Langmuir circulation, which can be optionally switched on. For this, the momentum equation is modified by including a vortex force and an additional advection by the Stokes drift following the theory by Craik and Leibovich (1976), similarly to McWilliams et al. (1997) and Skyllingstad and Denbo (1995). Furthermore, a simple parameterization of wave-breaking effects has been included. The modified momentum equations for the ocean then reads
where us is the Stokes drift velocity, ρθ the potential density, and the rotation of the velocity field. F is a random forcing term that represents the generation of small-scale turbulence by wave breaking. It should be kept in mind that the incompressibility assumption is used in the ocean option. It is assumed that wind stress and wave fields are in the same direction, and that the wave field is steady and monochromatic. The magnitude of the Stokes velocity along the wind stress direction is then given by
with , where zw is the wave height and λw is the wavelength. The current implementation of wave effects strictly follows Noh et al. (2004), in particular the parameterization of wave breaking. Note that Noh et al. (2004) used an earlier version of PALM, where the programming of the wave effects was completely realized via PALM's user interface.
As part of the general code modularization effort, all ocean-related code has been put into one Fortran module, and a separate namelist has been created containing all ocean-related steering parameters.
In this section, we first describe major revisions of the embedded models in the PALM core, namely in the bulk cloud microphysics parameterization (Sect. 3.1) and in the Lagrangian particle model (Sect. 3.3–3.4). Subsequently, we introduce three new embedded models in PALM 6.0: a fully interactive land surface model (LSM, Sect. 3.5), which can be coupled to two different radiation models (Sect. 3.6), and a parameterization scheme for taking into account the effect of wind turbines (Sect. 3.7).
3.1 Bulk cloud microphysics improvements
In PALM 4.0, the bulk liquid-phase (i.e., no ice) two-moment microphysics scheme of Seifert and Beheng (2001, 2006) was implemented, which only predicts the rain droplet number concentration () and rainwater mixing ratio (). This was extended by additional prognostic equations for the cloud droplet number concentration () and the cloud water mixing ratio () instead of using a fixed value for and only diagnostically calculated values for . The additional prognostic equations are thus given by
with the sink/source terms for and and the SGS fluxes:
The sink and source terms for and include the same microphysical processes as described by Maronga et al. (2015), namely autoconversion, accretion, and sedimentation of cloud droplets, as well as activation and diffusional growth, which has been newly added. Accordingly, the source and sink terms are given by
In the following, the source/sink terms for activation, condensation, and evaporation are described. This improved microphysics was recently applied by Schwenkel and Maronga (2019) for studying nocturnal radiation fog. Besides this physical improvement, the bulk microphysics is now fully modularized in PALM 6.0.
3.1.1 Activation of cloud droplets
As activation is the major source term for , this process is represented by so-called Twomey-type parameterizations in PALM 6.0, which are available in two modes. Per default, the number of activated cloud condensation nuclei (CCN) is given by a simple power-law expression:
where NCCN is the number of activated CCN, Na is the number concentration of the dry aerosol and the exponent kact depending on the type of analyzed aerosol (Twomey, 1959). The supersaturation over a liquid-phase surface is given by , where qv,sat stands for the water vapor saturation mixing ratio. Moreover, a more advanced method considering physiochemical properties of the dry aerosol can be used after Khvorostyanov and Curry (2006). Therein, it is assumed that the dry aerosol spectrum follows a log-normal distribution which is given by
where rd and rd,av are the radius and the mean radius of the dry aerosol, respectively. The dispersion of the dry aerosol spectrum is displayed by σd. Hence, the number of activated aerosol is calculated by
where “erf” is the Gaussian error function, and
A is the Kelvin parameter, and b and β depend on the chemical composition and physical properties of the soluble part of the dry aerosol. Both schemes have in common that Na must be prescribed and is calculated as a function of the aerosol concentration and the supersaturation. However, for the latter scheme, the physiochemical properties, such as the mean dry radius, chemical composition, and dispersion of the aerosol spectrum of the aerosol, must be prescribed by the user. The activation rate is then given by
where is the number of previously activated aerosols that are assumed to be equal to the number of pre-existing droplets and Δt is the length of the model time step. However, it must be mentioned that in regions with significant autoconversion and accretion growth, the subsequent depletion of might lead to an overprediction of activation with this method.
3.2 Improved representation of diffusional growth
Additionally, for treating condensational growth, a second method (diagnostic approach) apart from the well-established saturation adjustment scheme was implemented (see Maronga et al., 2015). This method diagnoses the current supersaturation from the fields of and . Subsequently, the diagnosed supersaturation is used for calculating the condensation and evaporation rates for cloud droplets, which is given by (Khairoutdinov and Kogan, 2000)
Here, rc is the volume mean radius of cloud droplets and Γ is a function of temperature and pressure including the thermal conduction and diffusion of water vapor in air. Ventilation effects which can affect the effective evaporation rates are considered for rain droplets separately, as described in Maronga et al. (2015). Note that this diagnostic scheme is an appropriate alternative, particularly if the assumptions made for saturation adjustment (assuming equilibrium) are violated, i.e., for time steps shorter than a few seconds.
3.3 Lagrangian particle model improvements
In the last years, the embedded LPM has been successfully used to study scalar dispersion in urban environments (e.g., Auvinen et al., 2017; Lo and Ngan, 2017; Gronemeier and Sühring, 2019). The LPM is based on Weil et al. (2004) to separate the particle speed into a deterministic and a stochastic contribution, which corresponds to dividing the turbulent flow field into a resolved-scale and a SGS portion, respectively. The resolved-scale velocity is provided by the LES at each time step, while the SGS velocity is predicted by integrating a stochastic differential equation according to Weil et al. (2004). For details on the model and its implementation, we refer to Steinfeld et al. (2008) and Maronga et al. (2015).
As particle boundary conditions at solid walls, PALM 6.0 offers absorption and reflection boundary conditions. The particle reflection boundary conditions were revised and adjusted to the revised topography implementation where also overhanging structures may appear. Now, within a time step, particles can be reflected multiple times at different solid walls, which is especially important near building corners.
Furthermore, the LPM was adjusted to the self-nesting (see Sect. 4.8). Particles that enter the region of one of the child domains are automatically transferred from the parent to the respective child model. Vice versa, particles leaving a child domain are automatically transferred back to its parent model. A technical description of this approach as well as implications concerning the treatment of SGS particle velocities when particles are transferred between parent and child will be discussed in a follow-up study.
3.4 Lagrangian cloud model improvements
PALM's Lagrangian cloud model (LCM) is based on its LPM, using Lagrangian particles as so-called superdroplets (e.g., Shima et al., 2009), each representing an ensemble of identical droplets that change their properties (e.g., water mass, aerosol mass, number of represented real droplets – the so-called weighting factor) by undergoing cloud microphysical processes. PALM's approach has been applied in various studies to further process-level understanding of warm-phase cloud microphysics, covering deliquescent aerosols, their entrainment and mixing with the cloud, as well as droplet activation, growth by diffusion, and collision and coalescence (Riechelmann et al., 2012; Hoffmann et al., 2015, 2017; Hoffmann, 2017; Noh et al., 2018).
3.4.1 Collision and coalescence
While the modeling of aerosol activation and diffusional growth of cloud droplets is based on first principles and is very similar in all available LCMs (Andrejczuk et al., 2008; Shima et al., 2009; Riechelmann et al., 2012), the representation of collision and coalescence (i.e., collection) depends heavily on model formulation. In a recent review paper, Unterstrasser et al. (2016) compared all available representations of collection in LCMs to analytical and other benchmark solutions. They showed that PALM's previous representation of collection is very stable but significantly underestimates the growth of the largest droplets, with commensurate effects on the initiation of rain. Therefore, our previous default collection algorithm by Riechelmann et al. (2012) was replaced by the so-called “all-or-nothing” algorithm that is based on the ideas of Shima et al. (2009) and Sölch and Kärcher (2010), and performed best in the comparison by Unterstrasser et al. (2016). The basic ideas of the all-or-nothing algorithm will be summarized below, but the interested reader is referred to Hoffmann et al. (2017) for more details on its implementation in PALM.
In the all-or-nothing approach, each real droplet of the superdroplet with the smaller weighting factor collects one real droplet of the superdroplet with the larger weighting factor. The probability P of this interaction is given by
where m and n are the indices of the superdroplets with the smaller and larger weighting factor, respectively, KK is the collection kernel depending on the properties of both superdroplets, ΔV is a prescribed volume in which the superdroplets are allowed the collide (which equals the size of an LES grid box in PALM), and Aw is the superdroplet weighting factor. If Pmn exceeds a random number chosen uniformly from the interval [0,1], the collection takes place. First, the mass of each real droplet of superdroplet m increases, while the mass of each real droplet of superdroplet n remains unchanged:
where the marks the variable after collection. Second, the aerosol mass of each real droplet changes:
Finally, the change in the weighting factor diverges from this pattern:
This procedure is repeated for all different (unordered) superdroplet pairs in the volume ΔV.
3.4.2 Splitting and merging of superdroplets
In recent studies with the LCM, it was observed that droplet size distributions does not converge even for large numbers (approximately 200) of superdroplets per grid box (e.g., Riechelmann et al., 2012). Based on the original idea of Unterstrasser and Sölch (2014), a splitting and merging algorithm for superdroplets has been adapted for our LCM. The main goal of such algorithms is to improve statistics by splitting one superdroplet into several superdroplets with the commensurate reduction of the weighting factor, and to save computational demand by merging several superdroplets into one superdroplet if appropriate. For a correct representation of the initiation of rain in warm clouds, a good statistical representation of collecting droplets by a sufficiently high number of superdroplets is indispensable.
The splitting algorithm is mainly steered by three parameters: (1) the minimum radius of superdroplets that will be split potentially, (2) a threshold for the weighting factor of that superdroplet (can either be prescribed or is approximated by assuming a gamma distribution; see Schwenkel et al., 2018), and (3) the splitting factor, which describes in how many particles one superdroplet will be split (prescribed or calculated by the LCM). However, the general splitting procedure is simple. If one superdroplet fulfills all criteria, the superdroplet is ηspl−1 times cloned and the weighting factor of the original and all new superdroplets is reduced to , while ηspl is the splitting factor, determining how many new superdroplets will be created during one operation. All other properties of the affected superdroplets remain unaffected. However, after a few time steps, every cloned superdroplet will experience slightly different subgrid-scale velocities and collisional growth rates due to the stochastic nature of these routines. Note that the splitting procedure is only applied in grid boxes where a threshold for the number of superdroplets per grid box is not exceeded to ensure computational feasibility. The merging algorithm is designed to save computational costs by merging superdroplets in regions where an increased superdroplet resolution is not required, e.g., outside of clouds. If a superdroplet grows smaller than a prescribed radius and exhibits a large enough (larger than a prescribed value) weighting factor, the superdroplet will be merged with another superdroplet in the same grid box that also fulfills these requirements. By doing so, the first superdroplet is deleted and the weighting factor of the other superdroplet is adapted to obey mass conservation. The splitting/merging algorithm is described in detail in Schwenkel et al. (2018). Their results show that the merging algorithm improves the representation of the collection process significantly, while decreasing computational time by up to 18 % compared to a simulation with a globally increased superdroplet number.
3.5 Land surface model (LSM)
LES models are often used with prescribed surface conditions (either by prescribing surface fluxes or by explicitly setting surface temperature and humidity). However, in many cases, an LSM is required in which the surface fluxes have to be calculated based on the state of the solid material (soil, water, pavement), the radiation budget of the surface, and atmospheric conditions. This might be the case when respective measurement data are absent, or when the interaction between atmosphere and surface becomes relevant, e.g., in the case of cloud or fog formation (Maronga and Reuder, 2017). Furthermore, LSMs are needed when the model is to be run in a forecasting mode, where surface boundary conditions are a priori unknown.
The implemented LSM in PALM is similar to the Tiled ECMWF Scheme for Surface Exchanges over Land (TESSEL/HTESSEL; Balsamo et al., 2009) and the derivative (simplified) implementation in the LES model DALES (Heus et al., 2010). The scheme implemented in PALM 6.0 was adapted for use with impervious surfaces (e.g., streets, pavements) as well as water surfaces, and was coupled to a radiation model (see Sect. 3.6) and both bulk cloud physics and Lagrangian cloud model (see Sect. 3.1 and Maronga et al., 2015).
The LSM consists of a solver for the energy balance of the Earth's surface using a resistance parameterization for the surface fluxes and a multi-layer soil scheme. The energy balance of the Earth's surface is calculated as
where C0 and T0 are the heat capacity and radiative temperature of the surface skin layer, respectively. Note that C0 is usually zero as it is assumed that the skin layer does not have a heat capacity (see below). Rn, H, LE, and G are the net radiation, sensible heat flux, latent heat flux, and ground (soil) heat flux at the surface, respectively.
H is calculated as
where ra is the aerodynamic resistance. θ0 and are the potential temperature at the surface and at a fixed height within the atmospheric surface layer (at height zmo), respectively. ra is calculated via MOST as
G is parameterized as (Duynkerke, 1999)
with Λ being the total thermal conductivity between skin layer and the uppermost soil layer. T0 is the radiative surface temperature (related to the radiative potential temperature via the Exner function) and Tsoil,1 is the temperature of the uppermost soil layer (calculated at the center of the layer). Λ is calculated via a resistance approach as a combination of the conductivity between the canopy and the soil-top (constant value) and the conductivity of the top half of the uppermost soil layer:
When no skin layer is used (i.e., in the case of bare soil and pavements), Λ reduces to the heat conductivity of the uppermost soil layer (divided by the layer depth). In that case, it is assumed that the soil temperature is constant within the uppermost 25 % of the top soil layer and equals the radiative temperature at the surface. C0 is then set to a non-zero value according to the material properties. The latent heat flux (LE) is calculated as
Here, rs is the surface resistance, qv,mo is the water vapor mixing ratio at height zmo, and qv,sat is the water vapor mixing ratio at saturation.
All equations above are solved locally for each surface element of the model grid. Each element for the surface-type vegetation can consist of patches of bare soil, vegetation, and a liquid water reservoir, which is the interception water stored on plants from precipitation. Therefore, an additional equation is solved for the liquid water reservoir. A liquid water reservoir is also available when the surface type is set to pavement, representing the ability of impervious surfaces to store a limited amount of liquid water at the surface. LE is then calculated for each of the three components (bare soil, vegetation, liquid water on plants/pavements). The resistance is calculated separately for bare soil and vegetation following Jarvis (1976).
For water surfaces, PALM currently only allows for prescribing a bulk water temperature. The energy balance is then solved as for land surfaces but without evapotranspiration from vegetation and bare soil. A skin layer is adopted so that C0=0 and in order to calculate a reasonable heat flux into the water body.
The surface is coupled to a 1-D soil model which is called independently for each surface element. By default, the soil model consists of eight layers with default layer depths of 0.01, 0.02, 0.04, 0.06, 0.14, 0.26, 0.54, and 1.86 m, (a variable number of layers and depths can be prescribed by the user) and in which the vertical heat and water transport is modeled using the Fourier law of diffusion and Richards' equation, respectively. Hydraulic conductivities are calculated after van Genuchten (1980). For vegetated surface elements, root fractions can be assigned to each soil layer to account for the explicit water withdrawal of plants used for transpiration from the respective soil layer. Viterbo and Beljaars (1995) and Balsamo et al. (2009) give more details.
Pavements are treated as a common soil (allowing varying depths of the pavement layers) but with physical properties of the pavement material. The pavement layer is impermeable and prohibits the vertical transport of soil moisture.
A first validation of a previous version of the LSM for simulation of nocturnal radiation fog is given in Maronga and Reuder (2017).
3.6 Radiation model
In simulations with LSM, or in cases where radiative effects of clouds are of interest, a suitable radiation parameterization is essential. This involves primarily the calculation of the surface radiation budget but also all radiative effects of clouds. PALM offers a built-in simple and fast radiation model for clear sky conditions that neglects the presence of humidity, clouds, and variations in aerosol and trace gas properties in the atmosphere. Moreover, PALM provides an interface to the shortwave and longwave components of the Rapid Radiative Transfer Model (for global models) (RRTMG; e.g., Clough et al., 2005). Both options calculate the radiation budget of the Earth's surface, which reads
where Rn is net radiation. SW↓, SW↑, LW↓, and LW↑ are the shortwave incoming (downward), shortwave outgoing (upward), longwave incoming (downward), and longwave outgoing (upward) fluxes, respectively.
3.6.1 Clear-sky radiation model
The clear-sky radiation model is a simple parameterization and limited to the calculation of the radiation budget at the surface. We recommend to use this scheme only for cases in which clouds are absent and in which direct cooling or heating of air due to divergence of the radiative fluxes is negligible. In the clear-sky model, SW↓ is calculated based on the position of the Sun and orbital parameters:
with S0=1368 W m−2 and Ψ being the solar constant and the cosine of the solar zenith angle, respectively. The transmissivity of the atmosphere τ is estimated to be
Ψ depends on UTC time (in seconds), day of the year (doy) and location, defined by geographical latitude ∘, 90∘] and longitude ∘, 180∘]. Ψ is calculated via
with
where d is the declination of the Sun, with
and the hour angle is given by
The flux (SW↑) depends on the incoming radiation (SW↓) and surface broadband albedo αbb (see Sect. 3.6.3):
The flux SW↑ is calculated from the Stefan–Boltzmann law:
where ϵ0 is the surface emissivity and W m−2 K−4 is the Stefan–Boltzmann constant.
The longwave incoming radiative flux is parameterized by a first-guess approximation:
with ϵatm=0.8 and Tmo being the bulk emissivity of the atmosphere and the absolute temperature at height zmo.
3.6.2 Coupling to RRTMG
As an advanced alternative to the clear-sky model, PALM can be used in combination with the RRTMG radiation code. The RRTMG source code is shipped along with PALM, but it is not part of the model (meaning that RRTMG is put under its own license). Unlike most embedded modules in PALM, the RRTMG is thus used as external library and linked to the default PALM code. The RRTMG subroutines are called from PALM as a 1-D model for each vertical column of the model grid. Vertical profiles of pressure, temperature, and water vapor volume mixing ratio are calculated in PALM and transferred to the radiation model. Moreover, information on clouds, namely the liquid water path and the effective droplet radius, is calculated by PALM and transferred to RRTMG. Concentrations of other trace gases are read during initialization from an input file. The standard profiles shipped with RRTMG are used by default. As RRTMG requires data up to the top of the atmosphere, the PALM data (i.e., θ, p, etc.) are extended and interpolated in the vertical direction by standard profiles, e.g., those shipped with RRTMG. In order to avoid large gradients at the interface between PALM's upper boundary and the upper atmospheric profiles, profiles are gradually blended over within the five grid points above the PALM domain.
RRTMG provides the shortwave and longwave radiative heating rates for each grid volume and the surface energy budget terms (see Sect. 3.5) and was first applied coupled to PALM by Maronga and Reuder (2017). When topographical elements are present at the surface, e.g., hills or buildings in urban area, it provides the radiation fluxes at the top boundary of the model for the radiative transfer model (RTM); see Sect. 4.4. As the default implementation of RRTMG does not provide the direct and diffuse irradiance, which are required for RTM, the original source code was modified so that they were available as outputs.
3.6.3 Calculation of surface albedos
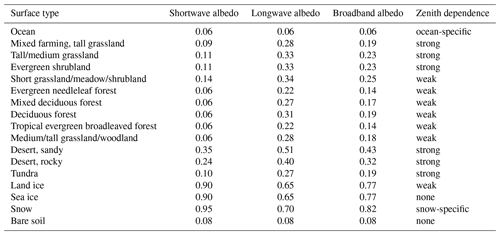
The calculation of the surface albedo components for longwave diffuse αlw,dif, longwave direct αlw,dir, shortwave diffuse αsw,dif, and shortwave direct αsw,dir radiation, as required by RRTMG, is parameterized according to Briegleb (1986) and Briegleb (1992). The parameterization involves dynamically changing the direct radiation albedos depending on Ψ, while diffuse radiation albedos are taken from a look-up table (see Table 7). The particular calculation of the albedo depends on a surface-type classification into classes of ocean, sea ice, snow, asphalt, and land surfaces with strong as well as weak zenith dependence on the albedo.
For ocean surface, the direct radiation albedo is calculated as
Snow surfaces have a zenith dependence, viz.
and
but have additionally an upper bound limit of 0.98. Albedos for land surface types are calculated as
and
Direct radiation albedos for surface of type sea ice, asphalt, and bare soil are set to be equal to those specified for diffuse radiation.
3.7 Wind turbine model
The rapid development of wind energy in the last two decades and the clear trend towards larger wind turbines and larger wind farms led to an increased interest in wake effects. The wake of a wind turbine is the region downstream of a wind turbine which is mainly characterized by a reduced wind speed and increased turbulence compared to the free stream. This means that a downstream wind turbine will produce less power if located in the wake of an upstream turbine. Increased wind shear and turbulence imply higher loads for downstream turbines, which can reduce the lifespan of turbine components. Wake effects are especially crucial in large wind farms where wakes of multiple turbines overlap. A detailed understanding of the wake effect and how the ABL affects the wake, and vice versa, is therefore very important for the wind industry from turbine manufacturers to planning companies to wind farm operators and traders. As turbulent processes in the ABL greatly affect wind turbine wakes (Vollmer et al., 2016), it may seem obvious to investigate wind farm flows with LES which can explicitly resolve most of the wake turbulence and its interaction with the ABL turbulence and thus serve as a virtual laboratory.
The wind turbine model (WTM) included in PALM is based on the common actuator disk model (ADM) approach in which the rotor of a wind turbine is represented by a permeable disk that extracts energy from the flow by applying a thrust force at the disk. While in the frequently used simple version of the ADM (e.g., as proposed by Calaf et al., 2010) the forces are uniformly distributed and only the thrust force is considered (thus ignoring the torque), the WTM provides an advanced ADM (ADM-R) based on blade element momentum theory that considers both thrust and torque as functions of the radial and tangential position on the rotor disk. The basic concept is similar to the ADM-R proposed by Wu and Porté-Agel (2011) with several modifications. The rotor plane is divided into annular segments as depicted in Fig. 1a). For the sake of clarity, only a few segments are shown. The segments have an equal size which is a function of the grid spacing. The default size is Δmin in tangential and 0.5Δmin in radial direction. For each segment, the local lift and drag forces (fl and fd) per unit area are calculated:
Urel is the local relative velocity in the center of the segment. It is calculated from the local wind speed components in axial and tangential direction, UN and Uθ (interpolated from the nearest grid points), and the velocity of the rotor blade segment Ωrseg as with the angular velocity of the rotor Ω and the distance of the segment from the center of the rotor disk rseg. cl and cd are the lift and drag coefficients of the blades, respectively, which are a function of the angle of attack of the local flow at the blade segment and thus vary in radial direction. The solidity factor Nbc∕(2πrseg) represents the fraction of time a segment would be covered by a blade (with the number of rotor blades Nb, the chord c). The blade properties (c, cl, and cd) are read from input namelist files in a specified format. By default, the WTM includes publicly available data for the National Renewable Energy Laboratory (NREL) 5 MW reference turbine (Jonkman et al., 2009) but it can easily be adapted for other turbine types, too. In a second step, the lift and drag forces are projected onto the axial and tangential directions to obtain the thrust fN and torque fΘ:
Here, ϕ is the angle between the local velocity components . These forces are then smeared and interpolated to the PALM grid points. To optimize the performance of the time-consuming smearing process, the smearing is done with a polynomial function instead of the standard Gaussian smearing and is confined to the region around the rotor. The effect of the tower and nacelle are considered by a simple drag force approach:
where fd,t and fd,n are the drag forces of the tower and the nacelle, respectively, with the drag coefficients and , and UN is the local axial velocity component. The forces (thrust, torque, and drag from tower and nacelle fl, fd, fd,t, and fd,t) are finally added as sink terms to the Navier–Stokes equations (Eq. 2).
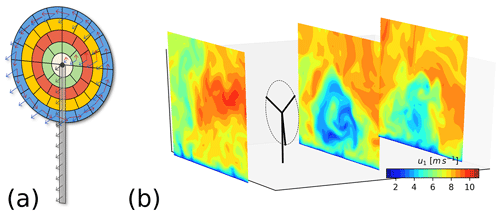
Figure 1(a) Schematic representation of the ADM-R model used in the WTM. Arrows denote the direction of the forces acting on the flow. (b) Example of a wake simulated with PALM-WTM. Shown is the instantaneous wind speed in mean flow direction (u component, inflow from the left).
The WTM contains a baseline rotational speed controller for the rotor of the wind turbine, implemented after Jonkman et al. (2009). The controller parameters are only valid for the NREL 5 MW reference turbine and need to be adjusted for different turbine types. The controller ensures that the wind turbine's power is following the constructor's power curve by adjusting the generator torque below and the blade pitch angles above the rated wind speed of the wind turbine. The wind turbine's electrical power is calculated from the torque and rotational speed of the rotor with the possibility to correct for generator and gearbox efficiency. Further details can be found in Jonkman et al. (2009). A yaw controller that ensures the automatic orientation of the wind turbine perpendicular to the wind is implemented following Storey et al. (2013).
Figure 1b shows a single turbine wake simulated by the PALM-WTM. The leftmost plane displays the turbulent inflow field. The near wake with its ring-shaped structure is visible in the central plane, while the far wake shown in the rightmost plane is more uniform, and the flow is starting to recover.
The WTM has already been used in a number of studies. Dörenkämper et al. (2015) simulated the offshore wind farm EnBW Baltic 1 and investigated the impact of the stable ABL on power production and wake effects. Vollmer et al. (2016) investigated the deflected wake behind a yawed wind turbine for different atmospheric stabilities. Vollmer et al. (2017) tried to reproduce the wind conditions around an offshore wind turbine by forcing the simulation with time series from a mesoscale model. They found a generally good agreement when comparing the PALM results with data from a meteorological mast and lidar measurements. Andersen et al. (2015) compared the results of the WTM and other LES models for very large idealized wind farms and explored how to best present and compare the resulting variability.
In this section, those modules are described which were newly implemented in the PALM model system. Note that PALM-4U components are essentially designed to be used for applications in urban environment, although they might as well be valuable for simulations without clear focus on urban processes.
4.1 Topography
Cartesian topography in PALM is considered using the mask method (Briscolini and Santangelo, 1989), where a grid cell is either 100 % fluid or 100 % obstacle. Fluid grid points are divided into grid points without adjacent surfaces where standard equations are solved, and surface-adjacent grid points where partly different code is executed, e.g., to represent wall functions. In former PALM versions, the topography masking was implemented using 2-D horizontal maps of vertical cell indices indicating the topography top at each grid point (x, y) on the staggered grid, effectively transforming a 3-D building and terrain topology into a 2.5-D topography. In this way, Cartesian topography was limited to surface mounted obstacles, forbidding overhanging structures such as bridges or tunnels. In order to overcome this limitation, PALM 6.0 uses a 3-D bit array to flag obstacles and surface-adjacent grid points. The individual terms of the standard governing equations are then solved at every model grid point. Obstacle grid points and, if required, surface-adjacent grid points are masked by multiplying the individual terms of the standard equations by zero. This revised Cartesian topography implementation enables full 3-D representation of obstacles, allowing for considering bridges or tunnel-like openings within buildings as recently studied by Gronemeier and Sühring (2019). A new Fortran derived-type data structure was implemented to efficiently store and compute data for complex surfaces (see Sect. 5.1).
4.2 Gas-phase chemistry
Gas-phase chemistry has been implemented into PALM 6.0 as an optional feature. When the gas-phase chemistry option is invoked, Nchem additional equations in analogy to Eq. (5) will be solved, with Nchem being the number of variable compounds of the chemical reaction scheme. The source/sink term therein for each chemical species includes emissions, chemical transformation, and deposition. This implementation permits the choice amongst gas-phase chemistry schemes of different complexity. Automatic generation of the chemistry code with the Kinetic Pre-Processor (KPP) version 2.2.3 (Damian et al., 2002) and an adapted version of the KP4 preprocessing tool (Jöckel et al., 2010) allows for high flexibility in the choice of gas-phase chemical mechanisms. Photolysis frequencies for reactions involving photochemistry are parameterized according to Saunders et al. (2003).
A number of predefined gas-phase chemical mechanisms of different complexity ranging from the photostationary state to the Carbon Bond Mechanism (CBM4) (Gery et al., 1989) are supplied with PALM. The source code for the chosen gas-phase chemistry mechanism is generated by utilizing the preprocessor prior to the compilation of the PALM-4U code. Due to the high computational demands, a compromise is necessary with respect to the degree of detail of the atmospheric chemistry. By default, the source code of PALM-4U is supplied with a chemistry module describing the photostationary equilibrium between NO, O3, and NO, plus the transport of a passive compound. The parameterization of dry deposition processes is implemented following the resistance approach. For gaseous compounds, the DEPAC module (Van Zanten et al., 2010) is used. Deposition of aerosols (PM10, PM2.5 was implemented following Zhang et al. (2001).
Emissions of gases and/or passive compounds can be provided in different levels of detail (LODs). Three modes were implemented, of which two require emission data from file and one is defined via a Fortran namelist and information from the static driver (see also Sect. 5.2.1). The latter, named “parameterized” mode, is currently only implemented for the traffic sector, in which emissions rely on a street-type classification provided by OpenStreetMap (https://www.openstreetmap.org, last access: 18 February 2020). For data from file, gridded emission information can be provided in two LODs in the desired netCDF format file (see also Sect. 5.2.1). LOD 1 files require annual emission information which are temporally disaggregated by PALM-4U using sector-specific time factors, while the LOD 2 files must contain temporally disaggregated emission information. Details of these three emission modes are provided in the online documentation of the PALM-4U chemistry module.
4.3 Aerosol physics
Aerosol physics were implemented based on the sectional aerosol module for large-scale applications (SALSA; Kokkola et al., 2008) which includes a detailed description of the aerosol number size distribution, chemical composition, and aerosol dynamic processes. This very aerosol module was chosen to be implemented in PALM due to SALSA's flexibility, and particularly since one major criterion in its development has been limiting computational expenses without the cost of accuracy.
In the aerosol module, a continuous aerosol size distribution function is discretized into a number of size bins (10 by default) based on the mean particle diameter, and each bin is further divided into different chemical components. The number and mass concentration of each chemical component in each bin are prognostic variables. Currently, the following chemical components can be included: sulfuric acid (H2SO4), organic carbon (OC), black carbon (BC), nitric acid (HNO3), ammonium (NH3), sea salt, dust, and water (H2O). By default, aerosol particles in one bin are considered internally mixed but it is possible to include externally mixed populations as well. The aerosol dynamic processes included are coagulation, nucleation, dry deposition on solid surfaces and resolved-scale vegetation, and condensation and dissolutional growth by gaseous H2SO4, HNO3, NH3, and semi- and non-volatile organics (SVOC and NVOC). These gas concentrations can be read to SALSA from the online chemistry module (Sect. 4.2).
The model implementation has been successfully evaluated against measurements on the vertical variation of the aerosol number size distribution and concentration in an urban environment. For details of the implementation and model evaluation, see Kurppa et al. (2019, this special issue).
4.4 Radiative transfer in complex environments
The RTM in PALM 6.0 calculates radiative interactions in geometrically complex environments like street-level urban canopy or complex terrain, and it represents a key component in modeling of energy exchanges for such scenarios. The RTM takes radiation from the radiation model (e.g., clear sky or RRTMG; see Sect. 3.6) on top of the complex urban or natural canopy layer, and it models the shortwave and longwave radiative processes inside this layer. It resolves shading, multiple reflections, emission, and absorption of radiation among surfaces and volumetric plant canopy within three-dimensional geometry. The resulting radiative fluxes are then supplied to the surface energy balance in the LSM and building surface modules (BSMs; see Sect. 4.5). Sensible heat from radiation absorbed inside the plant canopy is used to calculate the tendencies of the air potential temperature in volumes occupied with vegetation. The radiative fluxes inside the plant canopy are also used for the calculation of evapotranspiration and corresponding latent heat from trees. Moreover, the RTM models the mean radiant temperature and provides corresponding SW and LW fluxes to the biometeorology module for calculation of biometeorology indices (see Sect. 4.11).
The first version of RTM (1.0) appeared in PALM as a part of PALM-USM module (see Resler et al., 2017). The current version of RTM (3.0), which is part of PALM-4U 6.0, was significantly enhanced and it serves for calculation of radiative exchange among all surfaces (BSM as well as LSM surfaces). The enhancements of the new version include incorporation of new processes (e.g., interaction of longwave radiation with plant canopy), improved accuracy and scalability with new angular discretization scheme, as well as the significant improvement of performance via a new 2-D ray-tracing method and highly optimized parallelization.
4.4.1 Modeling of radiative processes
The RTM simulates radiative processes by calculating radiative fluxes between the Sun, sky, individual grid surface elements, and individual grid cells containing plant canopy. All radiative fluxes are modeled separately for shortwave and longwave radiation. The irradiance of each surface element is calculated using view factors (VFs), particularly sky view factors for diffuse radiation from the sky and surface view factors for reflected and emitted radiation. The plant canopy interaction with radiation is modeled via plant canopy sink factors (CSFs) which represent the portion of the radiation arriving from a particular source (e.g., the Sun, the sky, or a surface element) which is absorbed in a particular plant canopy grid cell.
The RTM uses the computational domain of PALM and its discretization and splitting among parallel Message Passing Interface (MPI) processes. The calculation of radiative interactions is split into two phases. The calculation of VFs, CSFs, and other time-invariant data, which represent a computationally demanding process, is done once during the initialization phase of the model so that the CPU, memory, and IPC demands for the following time-stepping phase are minimized. The calculation of the actual irradiance and heat fluxes is done during each radiation time step and it represents a computationally inexpensive process.
4.4.2 View factors and canopy sink factors
RTM 3.0 uses ray tracing together with angular discretization of view for calculation of radiative interactions. An optimized and parallelized 2-D ray-tracing algorithm is used to follow a fixed number of rays from each surface element or plant canopy grid cell, each of them representing an analytically determined portion of its view. The surface element that each ray strikes is used as a partial source of the target face's irradiance. The portion of view represented by the rays targeted above the horizon forms the target face's sky view factor, which describes irradiance by diffuse solar radiation and by the thermal radiation from the sky. The direct solar irradiance and shading is solved using precomputed ray paths for discretized apparent solar positions for simulation times.
Plant canopy is resolved as a fully three-dimensional structure of grid cells, each of which can have different leaf area density (LAD) and therefore different optical properties. The partial opacity of plant canopy grid cells means that the leaves of the trees and shrubs cover a portion of the view from the respective surface elements in the direction of the grid cell. When ray tracing, the grid cells with plant canopy are considered as partially opaque obstacles with transmittance ζ determined as
where γi is the radiant flux carried by the ray as it enters the grid cell, γt is the radiant flux carried by the ray as it leaves the grid cell, a is the leaf area density, lis is the length of the ray's intersection with the grid cell, and ξ is a constant extinction coefficient, which converts LAD of trees and shrubs into a corresponding average optical density. This information, determined during ray tracing, is stored as plant canopy sink factors. These factors are used to calculate the heat flux absorbed by plant canopy and also the longwave radiative flux emitted by the plant canopy in the direction of the respective surface element.
The process of each ray tracing represents a challenge for distributed memory parallel processing, as it requires data from different parallel subdomains stored in different MPI processes. With a fixed amount of traced rays per surface element in angular discretization, the amount of view factors grows with 𝒪(n2) and the amount of canopy sink factors grows with 𝒪(n3) if the resolution of the domain is increased by the factor of n in each dimension. Therefore, the computational and memory complexity of both the ray-tracing process and the time-stepping part of RTM is on par with scaling of other PALM-4U processes, and it represents a significant improvement over RTM 1.0, where the amount of view factors grew with 𝒪(n4) and amount of canopy sink factors grew with 𝒪(n5) in the worst case. The optimized 2-D ray-tracing algorithm processes all rays directed in one azimuth at once, which helps to significantly decrease computational demands and to optimize MPI data exchange patterns. With these optimizations, the time spent in RTM 3.0 represents a marginal portion of the total PALM-4U simulation time for typical scenarios (i.e., less than 5 % of the total computing time for the largest tested case domain with a horizontal extent of 1800×1800 m and 2 m resolution covering complex terrain of Prague's city center running at 1296 CPU cores).
4.4.3 Irradiance and absorption of radiation by plant canopy
The calculation of the irradiance and radiative heat fluxes is done during each radiation time step by the application of the precomputed view factors and canopy sink factors. The process starts by calculation of direct and diffuse radiation from the Sun and the sky, and it continues with the calculation of the configured number of the reflections after which all remaining radiative flux is considered as absorbed. The remaining flux can be verified in model outputs to be negligible.
Plant leaves have very high surface-to-mass ratio and they readily exchange heat with surrounding air via convection and evapotranspiration. Their temperature hence usually differs only marginally from the surrounding air. The current implementation of the RTM considers leaves as having zero thermal capacity and identical temperature as the surrounding air, which means that the difference of heat flux from absorbed minus emitted radiation is directly transferred to the air mass. This simplification represents a common approach (see, e.g., Dai et al., 2003).
Figure 2 illustrates the respective components of longwave and shortwave irradiance for a typical urban scenario during the summer day. It can be seen that the diffuse longwave irradiance from the sky and the thermal irradiance from other surfaces and plant canopy complement each other and that the shortwave direct solar component dominates the total radiative flux during daytime.
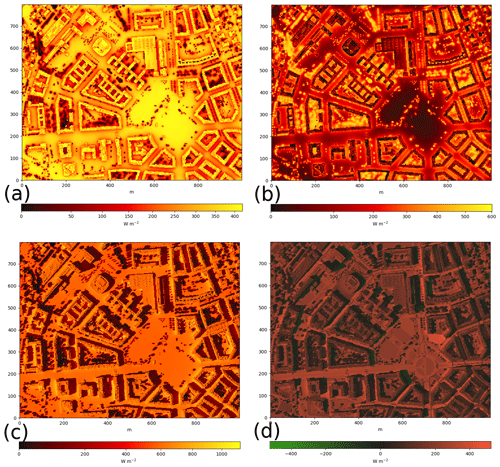
Figure 2Instantaneous radiative fluxes at horizontal surfaces in an urban area (Prague-Dejvice), 7 August 2015 at 14:30 UTC (approximately 15:30 solar time): (a) diffuse longwave irradiance from the sky; (b) longwave irradiance from other surfaces (reflected and emitted); (c) total shortwave irradiance (direct and diffuse solar, reflected); (d) broadband net radiative flux (absorbed minus emitted). Background: building heights are based on layer “relative building heights” freely available at the geoportal of Prague Institute of Planning and Development (http://www.geoportalpraha.cz/en/main, last access: 18 February 2020).
4.4.4 Calculation of plant canopy latent heat fluxes
An important part of the heat balance in the urban canopy represents the latent heat fluxes from the vegetation. The RTM explicitly computes the radiation balance for each grid cell of the volumetric plant canopy which allows to calculate the evapotranspiration of this vegetation.
The evapotranspiration of the resolved vegetation is modeled using the Jarvis–Stewart method (Stewart, 1988), implemented following Daudet et al. (1999) on the leaf level. The leaf evapotranspiration depends on the leaf boundary layer conductance and the stomatal conductance. The leaf boundary layer conductance is a function of the wind speed (Daudet et al., 1999). The stomatal conductance is a function of the incoming shortwave radiation, the air temperature, the water pressure deficit, and the relative soil water content following Stewart (1988)
After computing the evaporation per unit leaf area, the latent heat flux from leaves per the unit volume of vegetation is calculated by multiplication by the leaf area density (LAD). The sensible heat flux is the residual of the energy balance, neglecting the storage.
4.4.5 Coupling to the radiation model
The radiative transfer model is coupled to the radiation model by providing effective radiation surface parameters to the radiation model, which are used as its boundary conditions.
The idea of these effective radiation parameters is that they would, when applied to a simple single surface, give similar radiation fluxes to the complex 3-D urban area. The three effective parameters are the effective surface temperature T0,eff, the effective surface emissivity ϵeff, and the effective surface albedo αeff.
To derive these effective parameters, the lower boundary conditions of the radiation model for both longwave and shortwave radiation are considered as follows:
The energy conservation of longwave and shortwave radiation for the total urban area is used to derive Teff and αeff, while ϵ0,eff is chosen such that it represents the average of all urban surface emissivities.
4.5 Building surface model (BSM)
The BSM (formerly USM – urban surface model, and including pavements) represents the counterpart of the LSM described above for building surfaces (i.e., walls and roofs). The core of the module represents calculation of surface energy balance together with propagation of the thermal energy inside the building material and energy exchanges with indoor and outdoor environments. Anthropogenic waste heat, e.g., from transportation or industry, can be optionally prescribed by the user.
The initial version of the USM has been described in the paper of Resler et al. (2017). The paper outlines the principles of the USM as well and it presents the first validation of the model against thermal observations from an infrared camera for area of Prague-Holešovice. The current version of BSM model in PALM-4U 6.0 has been improved in several ways. The main improvement represents treatment of fractional surfaces. One fraction describes standard materials of the walls and roofs as in the original USM; the other fractions account for glass type of the surfaces (windows and other similar surfaces) and green elements on facades and roofs. Another substantial improvement represents the treatment of humidity and latent heat flux similarly to that in LSM (see Sect. 3.5).
Most of the BSM calculations follow the methods outlined for the LSM in Sect. 3.5. The window tile takes the transmissivity of the glass material into account by calculating its optical depth and using the Beer–Lambert law. The individual heat transfer properties of the different window layers are neglected and equal layer properties are calculated using the overall thermal transmittance. Green roofs (extensive or intensive) have underlying substrate layers where the temperature and heat transfer are taken into account. Green walls are considered facade-bound and are directly attached to the wall layers. The temperature and heat transfer within the material layers are calculated via the Fourier law of diffusion where the boundary condition on the outer surface is given by the surface energy balance, while the temperature on inner surface can be either prescribed in the configuration or is calculated by the indoor and building energy demand model (see Sect. 4.6).
The parameters of the urban canopy can be initialized with bulk parameters for specific building types or from a netCDF driver file (see Sect. 5.2.1). The current version of BSM also still includes the possibility to initialize these parameters through the legacy routines from CSV input files (see Resler et al., 2017). This option is, however, deprecated and will be removed in the near future.
4.6 Indoor and building energy demand model
There is a strong interaction between the urban energy balance with the building energy balance. The urban atmosphere acts on the heat transfer through exterior walls, the longwave heat transfer, the solar heat gains, and the ventilation. Considering also the internal heat gains and the heat capacity of the building structure, the energy balance of the interior building can be calculated based on an analytical solution of Fourier's law of heat conduction; see ISO 13790 (2008). The two main results are the energy demand for heating and cooling and the indoor thermal environment. According to the building energy concept, the energy demand results in an (anthropogenic) waste heat, which is directly transferred to the air adjacent to the building. The indoor temperature is re-coupled via the building envelope to the urban environment and is affected indirectly by the urban atmosphere with a time-shifted and damped temperature fluctuation.
Preliminary numerical and experimental studies clearly showed that different building concepts, their operation strategies, and urban structures have a strong impact on the urban heat island effect. Furthermore, numerical studies revealed the reaction of the urban heat island effect on the building energy balance (Pfafferott et al., 2011; Voss and Künz, 2012).
A holistic building model for the combined calculation of indoor climate and energy demand based on an analytic solution of Fourier's equation was implemented in PALM 6.0. The building model is integrated into the BSM (see Sect. 4.6). The interface between these two models is the temperature in the building envelope (i.e., the interior wall, window, or roof temperature). The building energy supply system is simulated with simplified models for different heating, cooling, ventilation, and/or air-conditioning concepts.
A commonly used database is used for the parameterization of both the facade and the building model (Institut Wohnen und Umwelt (IWU), 2005). Furthermore, the building database provides building physical parameters of the building envelope, geometry data, and operational data. The building description is based on geometry, fabric, window, and ventilation models for typical building types according to the year of construction or refurbishment, respectively. The user description is based on (stochastic) user behavior regarding window opening and use of solar control, and user profiles regarding attendance, heat gains (i.e., plug loads and lighting), metabolic rate, and clothing value. Energy efficiency factors and parameters related to the operation of the building energy system are defined for typical energy supply systems, e.g., district heating, boilers, heat pumps, or chillers.
The input information on building physical parameters from a regional survey or an urban planning tool is often uncertain and inconsistent. The model database is well structured and includes submodels which process information on different levels of accuracy and precision. Hence, the database is built up on a standardized building topology and can manually be adapted in order to evaluate measures with regard to the facade or to the building energy supply.
4.7 Surface spinup mechanism
When using either LSM or BSM, or both, it is often difficult to initialize the material temperatures (i.e., temperature of the individual soil, pavement, and building wall layers) and the soil moisture for natural surfaces. This is primarily due to the fact that such input data are unknown (e.g., wall temperatures of buildings) or only sparse measurement data are available (soils and pavements) from measurement campaigns. Furthermore, for idealized simulations, realistic initial material temperatures can have a strong effect on simulation results, particularly if only single diurnal cycles are simulated, which does not allow for a sufficient spinup period of the material layers.
In order to overcome such issues, PALM offers a surface spinup mechanism that allows for running long simulation periods as precursor to a full 3-D simulation. During such a spinup period, the atmospheric code of the model is switched off and only the radiation model, LSM, BSM, and optionally the indoor model are activated. This reduces the computational costs during the spinup phase by more than 90 %. The surface models are by design coupled to the atmosphere via the adjacent surface-parallel wind speed, temperature, and water vapor mixing ratio. During the spinup period, it is thus assumed that all surface elements are exposed to the wind profile at model initialization, thus considering stationary synoptic conditions. Furthermore, the wall-adjacent air temperature (i.e., θmo) is estimated by a simple sinusoidal diurnal cycle based on the cosine of the solar zenith angle that is calculated based on the geographical location, time, and two user-specific parameters:
Here, θsp,av and θsp,amp are the mean temperature and its amplitude in the diurnal cycle, respectively. These must be set explicitly by the user. A time lag of 1 h is imposed in order to account for a typical shift between maximum incoming solar radiation and maximum temperatures in the diurnal cycle. Note that humidity in the atmosphere is currently considered to be constant in time during the spinup phase and that there is no feedback of the surface scheme on the atmosphere during that period.
Figure 3Time series during an exemplary surface spinup of 3 d (72 h) starting on 3 March for a small LES setup, including different surface types and buildings, geographically located in Hannover, Germany. Panel (a) shows the surface forcing, imposed by an unobstructed incoming solar radiation and the subsequent near-surface potential temperature forcing, while panels (b) and (c) show the resulting material temperatures Tsoil for a soil covered by short grass and an asphalt pavement, respectively. The time axis denotes the hours until the start of the full 3-D atmospheric simulation. Note that the radiative forcing shown in panel (a) does not match the results shown in panel (b), where shadowing by buildings causes a drop in incoming shortwave radiation during afternoon hours.
Figure 3 shows exemplary results from a spinup for a test simulation with an urban setup and different surface types. The spinup simulation was 72 h and started on 3 March. The surface forcing calculated based on Eq. (93) is shown in Fig. 3a and reflects the time lag between maximum incoming radiation and maximum air temperature. Moreover, it is noticeable that the maximum values of SW↓ increase each day, which reflects the calendrical progress. Figure 3b, c show the time series of the material temperatures below a surface element covered with grass and an asphalt pavement, respectively. For the soil temperature below a grass canopy, we note a maximum temperature amplitude at the first grid level in the soil (here 0.005 m) of about 10 K, while the amplitude within the respective asphalt pavement is much higher (about 22 K). Furthermore, we can identify the expected time lag between different material layers, increasing with depth, and accompanied by a decrease in amplitude of diurnal temperature variations. Note also, that for the grass surface element, we note a stagnation or even drop in temperature in the afternoon hours. This is caused by a shadow cast by a nearby building, which is incorporated in the spinup. For both materials, temperature fluctuations at a depth of 0.8 m are negligible within the simulated time period and significant diurnal variations are only present within the uppermost 0.2 m within the material. Moreover, we note that for both surface types, the diurnal cycle of the uppermost material layer converges after 24 h of spinup, which is a typical result based on our experiences. Furthermore, it is evident that the initial material temperature distribution in the uppermost layer deviates from the one after 72 h by 4 and 6 K for short grass and pavement surfaces, respectively. This demonstrates the need for such a spinup to achieve equilibrium conditions at model initialization. As an ad hoc suggestion, especially for large simulation cases, where the spinup becomes computationally expensive, we thus recommend to use at least 24 h of spinup before starting the 3-D model.
4.8 Self-nesting
For LES of urban ABL including the urban canopy, high grid resolution is needed. Xie and Castro (2006) have shown that at least 15–20 grid nodes along one typical building length are needed to satisfactorily resolve the most important turbulent structures within street canyons. To meet this requirement, the grid spacing should typically be on the order of 1 m, while at the same time the vertical extent of the model domain should cover the whole ABL and the horizontal extent should span over several ABL heights in order to properly capture the dominant turbulent eddies in the ABL. Moreover, the uncertainty related to the lateral boundary conditions usually decreases as the domain becomes larger. Therefore, even larger domains are highly recommendable. However, using sufficiently high resolution in a sufficiently large domain often exceeds the available computational resources. In order to sufficiently resolve both the entire ABL and small-scale turbulent exchange processes within the areas of interest, a self-nesting capability was developed. Self-nesting here means that an instance of PALM can be nested into another instance of PALM. We prefer self-nesting to adaptive grid techniques, because it fits to PALM's Cartesian grid structure, it is easier to optimize, and because the areas of interest where high resolution is required are always known in advance.
The idea of PALM's self-nesting is to simultaneously run a series of two or more LES model domains with different spatial extents and grid resolutions. The outermost model is called the root model. The other models are called child models and their domains are nested completely inside the root domain. The root model is a parent model and contains at least one child model. Child models can be recursively nested within each other; i.e., a child model can have its own child models for which it acts as a parent model. A child model obtains boundary conditions for the prognostic quantities from its parent model through interpolation from the coarse to the fine grid. The self-nesting can be employed in a two-way or one-way mode. In the one-way coupled mode, only the child models obtain information from their parents, while the flow in the parent model is not affected by the child model solution. In contrast, in the two-way coupled nesting (default), the parent model is influenced by its child models through so-called anterpolation (Clark and Farley, 1984; Clark and Hall, 1991; Sullivan et al., 1996), where the fine-resolution child solution is transferred back to the parent domain. The anterpolation is implemented using the post insertion approach (Clark and Hall, 1991), which means that the parent solution is replaced by the child solution restricted onto the parent grid in the domain of overlap.
The bottom boundaries of all model domains do always follow the terrain/building surface; hence, the bottom boundary conditions are set in the usual way also for the child models. However, child model boundary conditions on the nested boundaries (left, right, south, north, and top boundaries) must be interpolated from the parent model. Concerning the interpolation method, it is important that the method conserves the mass-flow rate through the boundaries. If the mass conservation is violated in a two-way coupled run, a non-physical secondary circulation can develop. Clark and Farley (1984) developed a specific quadratic interpolation scheme that forms a reversible pair with the anterpolation scheme they employed. This reversibility guarantees the mass conservation. In PALM, the interpolation algorithm has to cope with complex topography. Therefore, we did not select the quadratic scheme of Clark and Farley (1984). Instead, we use the simple and robust zeroth-order interpolation in which constant values are set to the child grid nodes residing within a parent grid cell. This scheme readily guarantees mass conservation. Another reason for using the zeroth-order interpolation is that it generally leads to smaller conservation error of momentum and scalar fluxes than higher-order schemes.
The anterpolation scheme is similar to that of Clark and Farley (1984). For any scalar variable, the child grid values within a parent grid cell are averaged and the averaged value is mapped to the parent grid node. For the momentum component, the process is otherwise the same but because of the staggered grid arrangement, the parent grid cell is replaced by the two-dimensional cell face normal to the momentum component, i.e., the cell face where the momentum component is located. The anterpolation covers the whole volume occupied by the child domain except the parent grid layers nearest to the nested boundaries.
The nested model system is implemented using two levels of MPI communicators. The inter-model communication is handled by a global communicator using the one-sided communication pattern (remote memory access; RMA). The intra-model communication is two-sided and it is handled using a 2-D communicator. The intra-model communication system is the baseline parallelization of PALM (Maronga et al., 2015).
Beside an LES-LES self-nesting, also a RANS-RANS nesting is implemented (one-way and two-way), where the parent and the child models both solve the RANS equations, and an interchange of e as well as ϵ between parent and child is required. Moreover, note that also a one-way RANS-LES nesting is currently under development, where the child model obtains RANS-filtered boundary conditions for its prognostic variables (except for e) from the parent model. This way, synthetic turbulence is imposed at the lateral child boundaries to trigger the development of turbulence in the child model.
An example of the self-nesting feature within an urban boundary layer is shown in Fig. 4, where a child domain is nested in an array of cube-shaped building blocks. The figure demonstrates that much more small-scale turbulence, which is mainly generated by the building blocks, can be resolved in the child domain.
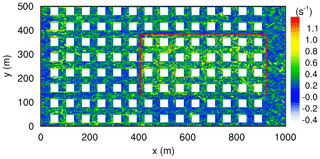
Figure 4Instantaneous horizontal cross section of the absolute value of the vorticity vector at a height of 10 m for a two-way LES–LES nested simulation of the turbulent flow around an array of cube-shaped buildings. The parent domain has a grid spacing of 2 m and the child domain (indicated by the red box) has a grid spacing of 1 m. The mean flow is parallel to the x axis from left to right.
Note that, while the 3-D self-nesting also can work in a 1-D manner, a separate method for pure 1-D nesting is implemented in PALM as described by Huq et al. (2018). In both cases, child and parent domains have identical horizontal dimensions and where the child obtains boundary conditions from the parent only at its top boundary. This 1-D self-nesting aims to improve the grid resolution near the surface throughout the entire horizontal extent of the domain.
4.9 Offline nesting
PALM has been successfully used to study non-stationary boundary layer processes with both idealized and realistic setups. For idealized setups with homogeneous flat terrain, cyclic boundary conditions are typically used at the lateral domain boundaries. This approach allows to study boundary layers not only under quasi-stationary but also under evolving synoptic conditions, which can be represented by additional advective and nudging terms (Heinze et al., 2017). The usage of cyclic boundary conditions, however, becomes problematic for heterogeneous complex natural and urban terrain, where the flow characteristics may depend on the upwind surface conditions and wakes or circulations that are generated within the model domain may re-enter at the upstream boundaries and cause unrealistic flow feedbacks. Large buffer zones around the domain of interest are often required in such cases (Maronga and Raasch, 2013; Letzel et al., 2012).
In order to enable simulations of realistic heterogeneous domains under evolving synoptic conditions, PALM 6.0 offers non-stationary Dirichlet boundary conditions, which can be provided by mesoscale interface INIFOR. INIFOR is a stand-alone pre-processor that derives realistic initial and boundary conditions for the PALM domain from the operational mesoscale weather prediction model COSMO-DE/D2 (Baldauf et al., 2011). The pre-processed output is stored in a dynamic driver (see Sect. 5.2.1), a netCDF file that PALM reads continuously during the model run to apply non-stationary boundary conditions. INIFOR interpolates all required meteorological fields onto the PALM grid. This includes the three wind components (, water vapor mixing ratio , and the potential temperature ). The meteorological variables are provided as hourly boundary conditions at the four lateral boundaries and the model top boundary. Initial conditions are provided either in the form of vertical profiles or as three-dimensional fields. INIFOR also derives the geostrophic wind profiles from COSMO's pressure field, which are used in the Boussinesq approximation to represent the evolving mesoscale pressure gradient, following the approach by Heinze et al. (2017). In addition to the meteorological variables, INIFOR also provides the initial soil temperature and moisture.
INIFOR can be used in combination with PALM's synthetic turbulence generator (see Sect. 2.3.3) to reduce the size of buffer zones that are needed to achieve fully developed turbulence in the inner domain. The synthetic turbulence imposed at the domain boundaries is continuously adjusted to the mean synoptic conditions. This is done by modifying the Reynolds stress that is used as an input in the turbulence generator, which is computed following Rotach et al. (1996). This way, changes in the stability regime and the meteorological conditions that may alter the amplitude and length scales of turbulent fluctuations are reflected in the synthetic inflow turbulence.
With the time-dependent setting of lateral and top boundary conditions in PALM, an automated mesoscale offline nesting of the PALM domain within the COSMO model is achieved.
4.10 Multi-agent system
Nowadays, more than half of the world's population lives in urban areas. Therefore, smart and sustainable city planning is required more and more. In this process, also the comfort of pedestrians is regarded, which strongly depends on the surrounding atmospheric environment. Typically, human comfort and quality of life from a meteorological perspective are judged on the basis of 2-D mapped indices (see Sect. 4.11). Taking these indices together with individual characteristics of a large number of pedestrians, like walking path and speed, age, clothing, etc., would enable the identification of areas for humans with high stress potential. Such hotspots cannot be determined from standard 2-D maps because they do not take into account peoples' behavior. Therefore, a Lagrangian-based multi-agent system (MAS) was developed and integrated into PALM, based on the concept of the already existing Lagrangian particle model (see Maronga et al., 2015). Using this model, it is possible to simulate individual pedestrians (agents) moving as part of a crowd coupled to the atmospheric code with the aim to evaluate quality of life on an individual level and studying environmental effects on large groups of people. In addition, the model provides the ability to simulate escape or evacuation scenarios coupled with the advanced method of LES used for turbulent dispersion of pollutants.
The MAS needs to perform a number of tasks to simulate the movement of pedestrians realistically. Firstly, agents must be able to navigate complex terrain to their individual targets, which includes the generation of a navigation graph from the Cartesian grid information present in PALM and a path-finding algorithm for navigating the graph. Secondly, local interactions of each agent with obstacles or other agents have to be considered.
The navigation graph is created in a preprocessing step from the Cartesian building configuration used in the PALM driver data. The tool calculating the graph (Agent Preprocessing Tool for PALM – APT-P) has been developed separately from PALM's model code. It is a stand-alone Fortran program, which is provided as a utility program shipped with PALM. The concept used in APT-P is called a visibility graph. It is based on the idea that pedestrians use outer corners of obstacles as navigation points for their movement. The agent will walk toward the next visible corner on their way to their final target, make a turn, and walk toward the next corner.
During the simulation, the MAS uses the visibility graph for navigating each agent individually from its current position to its target. This is accomplished using a path-finding method called the A∗ algorithm (Hart et al., 1968), which is able to find the optimal (fastest/shortest) path in a computationally efficient way concerning computation time and storage as well as to consider agent and target positions that were not previously stored on the visibility graph. To establish the path from the agent's current position to its target, the following steps are taken. (1) The agent's current position and its target are added to the visibility graph. (2) The shortest path between these two points is calculated using A∗. (3) The intermittent navigation points are shifted outward from the corresponding obstacle corner to a random position along a “gate” on the outer angle bisector of that corner to avoid collisions with obstacles or other agents. (4) Path finding (steps 1–4) is run again with each successive pair of navigation points along the path to avoid intersection of path sections with obstacles resulting from the outward shift. Finally, (5) the resulting path is stored in the agent object as a series of intermittent targets.
For each agent, the direction towards its next intermittent target is calculated for each agent time step. The agent will accelerate toward those coordinates, and once close enough, the next intermittent target is calculated. At the final target, the agent is deleted. Recalculation of an agent's path occurs when the agent has deviated too far from its current path, for example, through repulsion by obstacles or other pedestrians. Figure 5 shows the final result after applying the path-finding algorithm on the visibility graph.
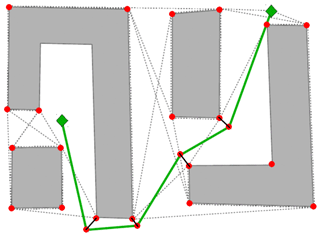
Figure 5Final result of the path-finding algorithm using the visibility graph created by the preprocessing tool (APT-P). The dots at the obstacle corners mark the nodes of the graph, and connections between these nodes, annotated with a cost to travel, are indicated by dashed lines. The left/right rhombus visualizes the starting/end point of the path to go, which is illustrated by green lines that are connected at the shifted navigation points. The outward shift of the original nodes toward the actual navigation points is visualized by black lines.
Once the fastest path is found, the individual agent movement and close-range interaction with obstacles and other pedestrians are realized using a Lagrangian-based social force model. Concepts from the original model formulation (Helbing and Molnár, 1995) as well as from its extension for close-range collision prediction and avoidance using a power-law approach (Karamouzas et al., 2014) have been adopted for the formulation of the MAS. The basic idea of the social force model is that pedestrian movement is the result of all forces acting on the pedestrian caused by its surroundings and goals. These forces can be either repulsive (e.g., buildings, trees, or other pedestrians) or attractive (e.g., current target, shop windows, or shaded areas on a hot day). The resulting force on a pedestrian α determines its acceleration. For time integration, a forward Euler method is used. As human reactions take place on a very short timescale and due to the chosen social forces approach, the time step for the agent model must be very short (approximately 0.02–0.04 s are recommended). In MAS, repulsion by obstacles and other pedestrians as well as the acceleration force driving the agent toward its target are considered. The formulation of both repulsion forces is based on an exponentially decreasing repulsive potential of the building's wall and other pedestrians, respectively. However, a further repulsive force was added to simulate collision avoidance behavior based on a universal power-law approach. It causes the agents to slow down, speed up, or slightly alter their path to avoid colliding with each other. Finally, the acceleration force, which accelerates an agent toward their current target, is implemented using a relaxation time that describes how quickly the pedestrian approaches the desired walking speed. For more information on the exact equations, see Helbing and Molnár (1995) and Karamouzas et al. (2014).
4.11 Human biometeorology
The livability of cities might be defined through the well-being of the human population, which is affected and interacting with the urban atmosphere. Biometeorological indices are a standard framework to assess this well-being (Staiger et al., 2019). The biometeorology module in PALM consists of two parts: A thermal comfort and a UV-exposure part. The thermal comfort part allows for the calculation of thermal indices approximating human thermal perception. Currently, the commonly used and well-validated indices of perceived temperature (PT; Staiger et al., 2012), universal thermal climate index (UTCI; Jendritzky et al., 2012; Bröde et al., 2012), and physiologically equivalent temperature (PET; Höppe, 1999) are supported, directly calculated in PALM, and used as output.
PT, UTCI, and PET follow a similar approach of equivalent temperatures. They generally calculate the overall energy gain or loss caused by the prevailing meteorological environment and transfer this to an “indoor” reference environment with all parameters set to static pre-known values, except for the air temperature. The air temperature is then set to a value that causes the same energy gain or loss as the actual meteorological environment. The air temperature of the reference environment is the returned as the result for the index. While the general concept of the indices is similar, the actual implementation is quite different. While, e.g., for PET, the environments are compared through the energy balance, in PT, the result of the simple indoor-only index predicted mean vote (PMV; Fanger, 1972) is compared. UTCI is determined in a simplified way by a regression equation after Bröde et al. (2012). Further major differences can be found in the definition of the sample person, as well as in the consideration of clothing insulation. The three indices are provided for the one horizontal cell level, which is the closest possible to 1.1 m above ground level (the average human gravity center; Fanger, 1972).
For the newly developed MAS (see Sect. 4.10), the thermal indices mentioned above cannot be used. They all do follow a steady-state approach, assuming long exposure of the sample person to constant environmental conditions (e.g., 2 h for PT). Therefore, a modified version of PT was implemented into the biometeorology module and coupled to the MAS. It aims at a better reproduction of the agents thermal stress caused by rapidly changing environmental conditions like radiation, wind speed, humidity and air temperature through consideration of the changes in the outer clothing surface temperature and a storage term in the energy balance.
With the exposure model of the UV-exposure part, calculations of biologically weighted human exposure in an urban environment can be performed. It is based on a three-dimensional voxel model of a human and the spectral radiance that takes into account the angular dependence of the radiation field (Seckmeyer et al., 2013). The spectral radiance was calculated by the DISORT code of the UVSPEC model in the LibRadTran package (Mayer and Kylling, 2005). The model consists of the four main input parameters: radiance, biological action spectrum (i.e., for erythema or vitamin D), human geometry, and effects by obstructions. The human geometry is taken into account by using a 3-D model based on a computer tomography scan of an average human adult (Valentin, 2002). For the calculation of the UV exposure in different seasons, the human model can be clothed in various ways, e.g., with typical winter or typical summer clothing. In addition, the model considers the effect of obstructions on the human exposure. Topographical elements (hills, vegetation, or buildings) cover various parts of the sky and hence block radiation from these directions (Schrempf et al., 2017). Therefore, the effects by topographical elements are determined for each grid point. This enables the calculation of realistic maps of human exposure in an urban environment and shows, for example, the vitamin D weighted human exposure depending on the time of day and season (i.e., position of the Sun), viewing direction, and the clothing of the human and the location within the city. An example of the exposure output is shown in Fig. 6, where a map of the vitamin D production of a human in Berlin (Germany) is shown.
Figure 6Vitamin D weighted exposure in IU per minute of a human on 21 June at noon in Berlin (Ernst-Reuter-Platz) under cloudless conditions. The human wears a T-shirt and pants and is oriented towards the south. Approximately 1000 IU per day are recommended as an adequate vitamin D status. Background: building height data created by DLR based on CityGML data from FIS Broker Berlin (https://www.stadtentwicklung.berlin.de/geoinformation/fis-broker/, last access: 18 February 2020).
5.1 Data structure for surface elements
At wall-adjacent grid points, additional code needs to be executed, e.g., for calculating the surface shear stress (see Sect. 2.3) and for the solution of the surface-energy balance to determine surface fluxes of sensible and latent heat. To efficiently access surfaces, we introduced a Fortran data structure that contains the relevant grid indices and the required surface variables, where all surface points located on a specific subdomain (i.e., one processor core) are stored consecutively in one-dimensional arrays. In this way, additional surface-related code parts, e.g., for the LSM (see Sect. 3.5), can be executed consecutively for all surfaces without adding “IF-ELSE” statements within the main loops that run over all grid points of the 3-D grid on the respective subdomain, which would hamper loop vectorization and reduce code legibility.
On the Cartesian grid oriented to the cardinal directions, surfaces can be horizontally aligned (facing upward or downward) or vertically aligned (facing northward, southward, eastward, or westward). Beside its orientation, surfaces are further distinguished between default-type surfaces (i.e., non-interactive), natural-type surfaces (water-, vegetation-, pavement-covered; see Sect. 3.5), and urban-type surfaces (buildings; see Sect. 4.5). At default-type surfaces, no energy balance is solved, and surface fluxes of sensible and latent heat can be either directly prescribed or computed by MOST by prescribing θ0 and q0. Note that the latter option is currently not implemented for downward and lateral-facing surfaces, as here the stability correction via MOST has no physical foundation (stratification is always considered as in the vertical direction in MOST and gravitational acceleration is always acting as a restraining force). For natural- and urban-type surfaces, the respective surface fluxes are calculated by solving the energy balance using the embedded land and urban surface model (see Sects. 3.5 and 4.5, respectively). Surfaces with different orientation and type are treated individually; i.e., surface properties and all relevant information are stored in individual data structures. Surfaces are automatically classified regarding their respective type and orientation depending on the input data (see Sect. 5.2.1), i.e., building and terrain height information.
5.2 Model operation and data handling
5.2.1 Model setup via netCDF input data
The original topography model in PALM (see Sect. 4.1) was implemented around 2008 and was provided to the model via an ASCII file containing the topography heights on a 2-D grid. The incorporation of full 3-D structures and interactive surfaces, however, requires setting of a great many of surface parameters like vegetation type, soil type, building height, building type, etc. for horizontal but also for vertical walls. Moreover, the applications have increased significantly in terms of number of grid points, rending the ASCII input of topography height inappropriate and inconvenient. While ASCII input is still partly supported, a new netCDF interface was introduced in PALM 6.0, which allows to define all surface-related parameters that do not change in time in a single netCDF file, the so-called static driver. These data can be provided for different LODs. For example, building heights can be prescribed as 2-D fields as in the deprecated ASCII input (LOD 1), but it is also possible to prescribe fully 3-D topography via a 3-D byte field (LOD 2). Moreover, each vegetated surface element can be defined through setting one of 17 predefined vegetation types, which trigger automatic setting of the parameters required by the LSM, like roughness lengths, emissivity, and leaf area index (LOD 1). Additionally, some or all of these automatically set parameters can individually be overwritten for each surface element (LODs 2 and 3).
In addition to static surface information, the stationary or time-dependent meteorological forcing for PALM 6.0 can be provided in a separate netCDF file (the so-called dynamic driver). The dynamic driver comprises all case-specific meteorological data, such as initialization data (e.g., wind and temperature as profiles or 3-D data, initial soil temperature and moisture), large-scale forcing tendencies, or time-dependent lateral boundary data. The new pre-processing tool INIFOR (see Sect. 4.9) can be employed to generate such dynamic drivers automatically based on COSMO data.
For PALM's chemistry model, emission data can be provided in analogy to the dynamic driver in a separate file, the so-called chemistry driver, which contains information on chemical compounds and their emission distribution in space and time.
The PALM input data standard (PIDS) provides a technical documentation on the static, dynamic, and chemistry drivers 1.
5.2.2 Model steering
The PALM model system offers shell scripts to compile and run the PALM code, including preparation and submission of batch jobs, job chains, and the handling of I/O files. The old ksh-shell scripts mbuild and mrun have been replaced by new bash-scripts palmbuild and palmrun. While the former scripts often required manual adjustments depending on the used MPI library and batch environment, the new scripts allow to run PALM on any batch system and with any MPI library without changing the scripts. All settings for the computing environment can now be provided via a configuration file called .palm.config.<ci>, where <ci> is the so-called configuration identifier. The scripts can use configuration files for different computing environments (compilers, libraries, batch systems, etc.), which are selected by the script option -c, e.g., palmrun -c intel_openmpi. The organization of I/O files (file names, file types, folder structure, etc.) is defined in a separate configuration file named .palm.iofiles. The complete script features and options are described in the online documentation.
5.2.3 Automatic model testing
The benefit of thorough software testing is higher software quality and reliability. In order to ensure high quality and reliability, PALM is now equipped with a test suite called palmtest. It is a Python-based software that automatically builds PALM according to specific build setups and executes PALM runs according to specific test cases. All the build setups and test cases are shipped within the PALM repository. The configuration of palmtest including all build setups and test cases is based on YAML files. Validation of the test results is done by comparing the generated results with reference files that are included in each of the test cases. These reference files are PALM output files and can be plain text files like the run control file as well as netCDF files. palmtest is capable of performing restarts by declaring dependencies between different test cases and using the restart data of one test case to initialize another test case. Note that palmtest is not capable of dealing with a batch system as it is intended to be used locally on a developers computer to ensure a healthy commit. palmtest is also executed on a central server after each commit to ensure the overall health of the main repository.
5.2.4 Virtual measurements
Virtual measurements in flow simulations are often used to verify and validate model components by comparing model results with in situ measurement data (e.g., Maronga et al., 2014; Heinze et al., 2017; Resler et al., 2017). Vice versa, virtual measurements can help to uncover deficiencies in measurement strategies by imitation and evaluation of different strategies (e.g., Sühring and Raasch, 2013; Maronga, 2014; Sühring et al., 2019). The advantages of numerical simulations are, e.g., that boundary and background conditions are known, and by means of ensemble runs or idealized simulation setups, more reliable statistics can be achieved. To emulate individual in situ observations at specific locations in realistically heterogeneous setups, however, a lot of manual work is required, e.g., to find out the respective grid indices. From the modeler's perspective, it is desirable to automatically translate observation coordinates into grid coordinates. From the analysis perspective, measured and simulated data should have the same format, variable naming, unit conventions, etc., enabling usage of the same analysis tools for in situ and virtually sampled datasets. For this purpose, PALM 6.0 provides a virtual-measurement module, which requires standardized information from measurement campaigns via netCDF file (see Sect. 5.2.1), i.e., the geographical coordinates, the used reference system, the sampled quantities in the atmosphere, soil, building walls, etc. The input and output format is specified in the data standard defined within the [UC]2 framework (see Sect. 5.2.5). The measurement coordinates for each site are translated into grid coordinates using the nearest model grid point instead of using interpolation to the exact site location. In order to minimize uncertainties due to biased geographical coordinates or errors in the model-surface or model-topography setup, data are additionally sampled at the surrounding grid points. Not only stationary measurement locations can be emulated but also trajectory (mobile) observations such as drone, car, bicycle, or pedestrian measurement systems. For a statistically more comprehensive picture, data are sampled along the entire trajectory at each model time step.
In order to avoid global communication during the simulation to merge the sample data for a site (for trajectory measurements, the relevant grid points might be distributed over several cores), the sampled data are written to one individual binary file per core. The PALM 6.0 model system provides a post-processor that merges the core-wise sampled data for each site and outputs the dataset into a separate netCDF file, resulting in one individual file for each measurement site.
5.2.5 Data output
Within the project framework of [UC]2, a data standard was developed for measurement and simulation datasets which inherits most of the netCDF Climate and Forecast Metadata Conventions version 1.7 (CF-1.7) (http://cfconventions.org/Data/cf-conventions/cf-conventions-1.7/cf-conventions.html, last access: 18 February 2020) and therefore also conforms with the conventions of the Cooperative Ocean/Atmosphere Research Data Service (COARDS)2 (Scherer et al., 2019b). The [UC]2 data standard describes precisely, among other parameters, the data type, naming of variables, and metadata which must be included in the datasets. PALM 6.0 data output is conformed to these data standards, as all data output is available in netCDF format including all requested metadata. Naming of variables also complies with the data standard and is constantly adjusted as the data standard grows to includes further variables. In this context, PALM 6.0 data output now also can include georeferencing (unlike prior PALM versions). Georeferencing includes UTM coordinates as well as geographical longitude and latitude of each horizontal grid point. Coordinates are calculated based on the given domain orientation and coordinates of a referencing point which is the front left grid point of the model domain.

Figure 7Surface net radiation flux in a built-up city quarter (Ernst-Reuter-Platz, Berlin, Germany) on 1 July 2009 at 14:00 UTC. Background: building height data created by DLR based on CityGML data from FIS Broker Berlin (https://www.stadtentwicklung.berlin.de/geoinformation/fis-broker/, last access: 18 February 2020).
In a complex environment with buildings and/or hilly terrain, natural and artificial surfaces are unevenly distributed within the model domain, with each processor possibly treating a different number of surfaces with different face orientation within its subdomain. Surface data are output into netCDF files as one-dimensional arrays (see also Sect. 5.1). To unambiguously identify surfaces, also their grid coordinates as well as their orientation relative to zenith and azimuth are output. Further, to visualize surface data, e.g., the surface temperature or radiation fluxes, we additionally implemented an appropriate output format into PALM 6.0 based on the Visualization Toolkit (VTK) format (Schroeder et al., 2006). Therefore, as a first step, the vertices of the surface elements and the polygons spanned by these vertices, which unambiguously define the Cartesian wall/land surface elements, are written to individual binary output files by each processor for its subdomain. Secondly, the surface data for an output quantity are gathered from the different surface types and orientations (see Sect. 5.1) at each output time step and also written to individual binary output files by each processor. PALM 6.0 provides a post-processing tool to merge the binary output data from all subdomains and to convert these according to the VTK file format. This format enables to analyze and visualize the surface data with well-known tools such as ParaView (https://www.paraview.org/, last access: 18 February 2020). An example of the surface-data output is shown in Fig. 7, where the surface net radiation flux is illustrated in a built-up city quarter in Berlin, Germany. Figure 7 indicates the shading of the direct solar radiation at horizontal surfaces and facades, as well as the effect of different surface properties on the surface radiation balance (see, e.g., the region near the roundabout in the center of Fig. 7).
5.3 Model optimization
Optimization efforts since PALM 4.0 were mainly targeted on allowing better code vectorization by compilers for Intel and AMD processor units. Within the red-black algorithm of the multigrid Poisson solver, the grid point values with even and odd indices are calculated alternately for each dimension of the 3-D array. This results in loops programmed with a stride of 2. On recent Intel processor generations, different flavors of vector units were implemented. Starting with AVX on Ivybridge, the current Skylake processor includes AVX512 units. Common to all AVX units is that scattered data access is either not implemented or ineffective. In order to enable a vectorization of the red-black algorithm, a re-sorting of the k dimension of the respective 3-D arrays is done. For this, the values with even indices are stored in the lower half and the values with odd indices are stored in the upper half of the k-dimension vector. Now, loops can run with stride 1 along k and the red-back algorithm vectorizes completely. This vectorization results in an overall speedup of more than 10 % (for a test run with grid points in x, y, and z directions, respectively).
In this overview paper, we gave an overview of the PALM model system 6.0. We described in detail the revisions made compared to PALM 4.0, which was described in the precursor paper of Maronga et al. (2015). As this paper was designed also as an overview paper for the PALM 6.0 special issue in this journal, we gave a rather brief summary of those parts for which companion papers will be submitted (or already have been) to this special issue. For all other new features and revisions, we gave a more detailed description.
PALM 6.0 represents a tremendous enhanced and improved model system compared to its predecessor version. It does not only include improved model core physics like additional turbulence closure schemes, extended cloud microphysics, a wind turbine parameterization, and a fully interactive and coupled surface-radiation scheme, but also new components to enable in-depth simulations of urban environments (so-called PALM-4U components). Above all, this involves a building surface and indoor model, gas-phase chemistry and aerosol physics, and output of biometeorological indices. Furthermore, technical developments like two-way self-nesting and offline coupling to the large-scale model COSMO enable large simulation domains that allow to resolve the (turbulent) flow at very high spatial resolution in areas of special interest. While this is particularly useful for urban simulations, it will also be beneficial for other PALM applications.
While we focused on the technical description of the technical innovations in PALM 6.0, we did not address the topic of model validation in this paper in much detail, though it is of course a critical aspect in model development. During four intensive observation periods in the framework of [UC]2 (see Scherer et al., 2019a), an unprecedented database of measurement in an urban area was created. Also, wind tunnel data were collected by the University of Hamburg, Germany. This database will be used to evaluate the new PALM-4U components based on large-scale PALM runs for the cities of Berlin, Hamburg, and Stuttgart. We will make use of the newly developed virtual measurement module to allow for one-to-one comparison with observational data. Further validation efforts are reported in the companion papers in this special issue.
Despite these model extensions, most of which developed in the context of the [UC]2 program, there is urgent need for further enhancements. For example, there is currently no parameterization for frozen water in PALM. Ice clouds as well as snow on surfaces or frozen water in the soil can thus not be simulated, imposing limitations for applications in regions prone to low temperatures and snowfall during wintertime. Also, precipitation, though included for warm clouds in the PALM core, is currently not available together with urban surface configurations, above all, because of the missing incorporation in the RTM. Moreover, several chemistry improvements regarding biogene volatile organic compounds, pollen transport, and improved aerosol description (including ultra-fine particles) would be desirable. The multi-agent system might be further developed and it is planned to couple it to the traffic flow model MATSim (Horni et al., 2016) that allows for more detailed traffic emissions. Vehicle-induced turbulence is known to be a key process for the dispersion of pollutants emitted by vehicles that is often parameterized in RANS-type models. For LES, however, there currently is no suitable parameterization available to account for the additional mixing by vehicles. This could be either accounted for by explicitly placing moving car-like objects in the LES domain or by developing a new parameterization scheme suitable for LES models. Furthermore, important processes for urban climate studies are lacking, like a model to predict wind throw in stormy weather or sound emission and propagation, among others. Also, the Cartesian topography model in PALM currently implies that slanted roofs and walls are represented by step-like structures, which could be avoided by implementing an immersed boundary method (Mason and Sykes, 1978).
We aim to complete the model system by further developments as outlined above within a possible second funding phase of [UC]2. In that course, we also plan to create a sustainable community model governance structure and will make significant effort to further strengthen PALM's position in the boundary layer and urban climate scientific community.
| Abbreviation | Description |
| [UC]2 | Urban Climate Under Change |
| ABL | Atmospheric boundary layer |
| ADM | Actuator disk model |
| ADM-R | Rotating actuator disk model |
| APT-P | Agent Preprocessing Tool for PALM |
| BSM | Building surface model |
| CCN | Cloud condensation nuclei |
| CSF | Canopy sink factor |
| LAD | Leaf area density |
| LCM | Lagrangian cloud model |
| LES | Large-eddy simulation |
| LOD | Level of detail |
| LPM | Lagrangian particle model |
| LSM | Land surface model |
| MAS | Multi-agent system |
| MOST | Monin–Obukhov similarity theory |
| MPI | Message Passing Interface |
| PET | Physiologically equivalent temperature |
| PMV | Predicted mean vote |
| PT | Perceived temperature |
| RANS | Reynolds-averaged Navier–Stokes |
| RTM | Radiative transfer model |
| SGS | Subgrid scale |
| SGS-TKE | Subgrid-scale turbulence kinetic energy |
| TKE | Turbulence kinetic energy |
| USM | Urban surface module |
| UTCI | Universal thermal climate index |
| VF | View factor |
| WTM | Wind turbine model |
The PALM model system is freely available from http://palm-model.org (last access: 18 February 2020) and distributed under the GNU General Public License v3 (http://www.gnu.org/copyleft/gpl.html, last access: 18 February 2020). The model source code of version 6.0 in revision 3668, described in this article, is also available via https://doi.org/10.25835/0041607 (Maronga, 2019). For code management, versioning, and revision control, the PALM group runs an Apache Subversion (http://subversion.apache.org, last access: 18 February 2020) (svn) server. The PALM model system can be downloaded via the svn server, which is also integrated in a web-based project management and bug-tracking system using the software Trac (http://trac.edgewall.org, last access: 18 February 2020). In this way, PALM users can use the web interface to browse through the code, view recent code modifications, and submit bug reports via a ticketing system directly to the code developers. Furthermore, a model documentation, a detailed user manual, as well as an online tutorial are available on the Trac server and are constantly kept up to date by the PALM developers. Code updates and development are generally reserved to the PALM developers and supervised by the PALM administration at the Institute of Meteorology and Climatology at Leibniz University Hannover in order to keep the code structure clean, consistent, and uniform. However, we encourage researchers to contact us for collaborative code development that might be suitable to enter the default PALM model system. We also appreciate suggestions for future PALM model system developments.
The PALM model system 6.0 is a joint effort by several institutions and developers, most of which are authors of this paper. BM designed, prepared, and edited the manuscript with contributions by all listed co-authors.
The authors declare that they have no conflict of interest.
We would like to thank the two anonymous reviewers for their helpful comments on the manuscript. The German Aerospace Center (DLR) Project Management supports the consortium. Benchmark and test runs with PALM have been performed at the supercomputers of the North-German Supercomputing Alliance (HLRN), which is gratefully acknowledged. The co-authors Jaroslav Resler, Pavel Krč, Jan Geletič, and Vladimir Fuka were supported by the project URBI PRAGENSI CZ.07.1.02/0.0/0.0/16_040/0000383 under the program OP PPR “Prague – Growth Pole of the Czech Republic” which is co-financed by EU. Some of the simulations were done on the supercomputer Salomon, which was supported by the Ministry of Education, Youth and Sports of the Czech Republic from the Large Infrastructures for Research, Experimental Development and Innovations project “IT4Innovations National Supercomputing Center – LM2015070”. The co-author Antti Hellsten was supported by Academy of Finland (grant agreement 277664) and the co-author Mona Kurppa by the doctoral program in Atmospheric Sciences (ATM-DP, University of Helsinki) and the Helsinki Metropolitan Region Urban Research Program.
This research has been supported by the Federal Ministry of Education and Research (Germany) (grant no. 01LP1601A). [UC]2 is funded by the German Federal Ministry of Education and Research (BMBF) under grant 01LP1601 within the framework of Research for Sustainable Development (FONA; https://www.fona.de/de/, last access: 18 February 2020), which is greatly acknowledged.
The publication of this article was funded by the open-access fund of Leibniz Universität Hannover.
This paper was edited by Richard Neale and reviewed by two anonymous referees.
Andersen, S. J., Witha, B., Breton, S.-P., Sørensen, J. N., Mikkelsen, R. F., and Ivanell, S.: Quantifying variability of Large Eddy Simulations of very large wind farms, J. Phys. Conf. Ser., 625, 012027, https://doi.org/10.1088/1742-6596/625/1/012027, 2015. a
Andrejczuk, M., Reisner, J. M., Henson, B., Dubey, M. K., and Jeffery, C. A.: The potential impacts of pollution on a nondrizzling stratus deck: Does aerosol number matter more than type?, J. Geophys. Res., 113, D19204, https://doi.org/10.1029/2007JD009445, 2008. a
Arakawa, A. and Lamb, V. R.: Computational design of the basic dynamical processes of the UCLA general circulation model, in: General circulation models of the atmosphere, Methods in computational physics, edited by: Chang, J., Elsevier, 17, 173–265, https://doi.org/10.1016/B978-0-12-460817-7.50009-4, 1977. a
Auvinen, M., Järvi, L., Hellsten, A., Rannik, Ü., and Vesala, T.: Numerical framework for the computation of urban flux footprints employing large-eddy simulation and Lagrangian stochastic modeling, Geosci. Model Dev., 10, 4187–4205, https://doi.org/10.5194/gmd-10-4187-2017, 2017. a
Baldauf, M., Seifert, A., Förstner, J., Majewski, D., Raschendorfer, M., and Reinhardt, T.: Operational Convective-Scale Numerical Weather Prediction with the COSMO Model: Description and Sensitivities, Mon. Weather Rev., 139, 3887–3905, https://doi.org/10.1175/MWR-D-10-05013.1, 2011. a
Balsamo, G., Vitebo, P., Beljaars, A., van den Hurk, B., Hirschi, M., Betts, A. K., and Scipal, K.: A revised hydrology for the ECMWF model: Verification from field site to terrestrial water storage and impact in the Integrated Forecast System, J. Hydrometeorol., 10, 623–643, 2009. a, b
Basu, S. and Lacser, A.: A Cautionary Note on the Use of Monin–Obukhov Similarity Theory in Very High-Resolution Large-Eddy Simulations, Bound. Lay.-Meteorol., 163, 351–355, https://doi.org/10.1007/s10546-016-0225-y, 2017. a
Beljaars, A.: The parametrization of surface fluxes in large-scale models under free convection., Q. J. Roy. Met. Soc., 121, 255–270, 1994. a
Blackadar, A. K.: The vertical distribution of wind and turbulent exchange in a neutral atmosphere, J. Geophys. Res., 67, 3095–3102, https://doi.org/10.1029/JZ067i008p03095, 1962. a, b
Briegleb, B. P.: Comparison of regional clear-sky albedos inferred from satellite observations and model computations, J. Climate Appl. Meteorol., 25, 214–226, 1986. a
Briegleb, B. P.: Delta-Eddington approximation for solar radiation in the NCAR community climate model, J. Geophys. Res., 97, 7603–7612, https://doi.org/10.1029/92JD00291, 1992. a
Briscolini, M. and Santangelo, P.: Development of the mask method for incompressible unsteady flows, J. Comp. Phys., 84, 57–75, 1989. a, b
Bröde, P., Fiala, D., Błazejczyk, K., Holmér, I., Jendritzky, G., Kampmann, B., Tinz, B., and Havenith, G.: Deriving the operational procedure for the Universal Thermal Climate Index (UTCI), Int. J. Biometeorol., 56, 481–494, https://doi.org/10.1007/s00484-011-0454-1, 2012. a, b
Calaf, M., Meneveau, C., and Meyers, J.: Large eddy simulation study of fully developed wind-turbine array boundary layers, Phys. Fluids, 22, 015110, https://doi.org/10.1063/1.3291077, 2010. a
Clark, T. L. and Farley, R. D.: Severe downslope windstorm calculations in two and three spatial dimensions using anelastic interactive grid nesting: A possible mechanism for gustiness, J. Atmos. Sci., 41, 329–350, 1984. a, b, c, d
Clark, T. L. and Hall, W. D.: Multi-domain simulations of the time dependent Navier-Stokes equations: benchmark error analysis of some nesting procedures, J. Comp. Phys., 92, 456–481, 1991. a, b
Clough, S. A., Shephard, M. W., Mlawer, E. J., Delamere, J. S., Iacono, M. J., Cady-Pereira, K., Boukabara, S., and Brown, P. D.: Atmospheric radiative transfer modeling: A summary of the AER codes, Short Communication, J. Quant. Spectrosc. Ra., 91, 233–244, 2005. a
Craik, A. D. D. and Leibovich, S.: A rational model for Langmuir Circulations, J. Fluid Mech., 73, 401–426, 1976. a
Dai, Y., Zeng, X., Dickinson, R. E., Baker, I., Bonan, G. B., Bosilovich, M. G., Denning, A. S., Dirmeyer, P. A., Houser, P. R., Niu, G., Oleson, K. W., Schlosser, C. A., and Zong-Liang, Y.: The common land model, B. Am. Meteorol. Soc., 84, 1013–1024, 2003. a
Damian, V., Sandu, A., Damian, M., Potra, F., and Carmichael, G. R.: The kinetic preprocessor KPP – a software environment for solving chemical kinetics, Comput. Chem. Eng., 26, 1567–1579, 2002. a
Daudet, F. A., Le Roux, X., Sinoquet, H., and Adam, B.: Wind speed and leaf boundary layer conductance variation within tree crown: consequences on leaf-to-atmosphere coupling and tree functions, Agr. Forest Meteorol., 97, 171–185, 1999. a, b
Deardorff, J. W.: A numerical study of three-dimensional turbulent channel flow at large Reynolds number, J. Fluids Mech., 31, 453–480, 1970. a
Deardorff, J. W.: The use of subgrid transport equations in a three-dimensional model of atmospheric turbulence, J. Fluids Eng., 95, 429–438, 1973. a
Deardorff, J. W.: Stratocumulus-capped mixed layers derived from a three-dimensional model, Bound.-Lay. Meteorol., 18, 495–527, 1980. a
Dörenkämper, M., Witha, B., Steinfeld, G., Heinemann, D., and Kühn, M.: The impact of stable atmospheric boundary layers on wind-turbine wakes within offshore wind farms, J. Wind Eng. Ind. Aerod., 144, 146–153, https://doi.org/10.1016/j.jweia.2014.12.011, 2015. a
Duynkerke, P. G.: Turbulence, radiation and fog in Dutch stable boundary layers, Bound.-Lay. Meteorol., 90, 447–477, https://doi.org/10.1023/A:1026441904734, 1999. a
Fanger, P. O.: Thermal comfort, McGraw-Hill, New York, 1972. a, b
Germano, M., Piomelli, U., Moin, P., and Chabot, W. H.: A dynamic subgrid-scale eddy viscosity model, Phys. Fluids A-Fluid, 3, 1760–1765, 1991. a
Gery, M. W., Whitten, G. Z., Killus, J. P., and Dodge, M. C.: A Photochemical Kinetics Mechanism for Urban and Regional Scale Computer Modeling, J. Geophys. Res.-Atmos., 26, 12925–12956, https://doi.org/10.1029/JD094iD10p12925, 1989. a
Gronemeier, T. and Sühring, M.: On the effects of lateral openings on courtyard ventilation and pollution – a large-eddy simulation study, Atmosphere, 10, 63, https://doi.org/10.3390/atmos10020063, 2019. a, b
Gronemeier, T., Inagaki, A., Gryschka, M., and Kanda, M.: Large-Eddy Simulation of an Urban Canopy Using a Synthetic Turbulence Inflow Generator Method, ournal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering), 71, 43–48, https://doi.org/10.2208/jscejhe.71.i_43, 2015. a
Gronemeier, T., Raasch, S., and Ng, E.: Effects of Unstable Stratification on Ventilation in Hong Kong, Atmosphere, 8, 1–15, https://doi.org/10.3390/atmos8090168, 2017. a, b
Harlow, F. H. and Welch, J. E.: Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface, Phys. Fluids, 8, 2182–2189, 1965. a
Hart, P. E., Nilsson, N. J., and Raphael, B.: A Formal Basis for the Heuristic Determination of Minimum Cost Paths, IEEE Trans. Syst. Sci. Cybern., 4, 100–107, https://doi.org/10.1109/TSSC.1968.300136, 1968. a
Heinz, S.: Realizability of dynamic subgrid-scale stress models via stochastic analysis, Monte Carlo Meth. Appl., 14, 311–329, 2008. a, b, c
Heinz, S. and Gopalan, H.: Realizable versus non-realizable dynamic subgrid-scale stress models, Phys. Fluids, 24, 115105, https://doi.org/10.1063/1.4767538, 2012. a
Heinze, R., Moseley, C., Böske, L. N., Muppa, S. K., Maurer, V., Raasch, S., and Stevens, B.: Evaluation of large-eddy simulations forced with mesoscale model output for a multi-week period during a measurement campaign, Atmos. Chem. Phys., 17, 7083–7109, https://doi.org/10.5194/acp-17-7083-2017, 2017. a, b, c
Helbing, D. and Molnár, P.: Social force model for pedestrian dynamics, Phys. Rev. E, 51, 4282–4286, https://doi.org/10.1103/PhysRevE.51.4282, 1995. a, b
Heus, T., van Heerwaarden, C. C., Jonker, H. J. J., Pier Siebesma, A., Axelsen, S., van den Dries, K., Geoffroy, O., Moene, A. F., Pino, D., de Roode, S. R., and Vilà-Guerau de Arellano, J.: Formulation of the Dutch Atmospheric Large-Eddy Simulation (DALES) and overview of its applications, Geosci. Model Dev., 3, 415–444, https://doi.org/10.5194/gmd-3-415-2010, 2010. a, b
Hoffmann, F.: On the limits of Köhler activation theory: how do collision and coalescence affect the activation of aerosols?, Atmos. Chem. Phys., 17, 8343–8356, https://doi.org/10.5194/acp-17-8343-2017, 2017. a
Hoffmann, F., Raasch, S., and Noh, Y.: Entrainment of aerosols and their activation in a shallow cumulus cloud studied with a coupled LCM-LES approach, Atmos. Res., 156, 43–57, 2015. a
Hoffmann, F., Noh, Y., and Raasch, S.: The route to raindrop formation in a shallow cumulus cloud simulated by a Lagrangian cloud model, J. Atmos. Sci., 74, 2125–2142, 2017. a, b
Holt, T. and Raman, S.: A review and comparative evaluation of multilevel boundary layer parameterizations for first-order and turbulent kinetic energy closure schemes, Rev. Geophys., 26, 761–780, 1988. a
Holtslag, A. A. M. and De Bruin, H. A. D.: Applied modelling of the night-time surface energy balance over land., J. Appl. Meteorol., 27, 689–704, 1988. a
Höppe, P. R.: The physiological equivalent temperature – a universal index for the biometeorological assessment of the thermal environment, Int. J. Biometeorol., 43, 71–75, 1999. a
Horni, A., Nagel, K., and Axhausen, K. W.: The Multi-Agent Transport Simulation MATSim, Ubiquity, London, 2016. a
Hultmark, M., Calaf, M., and Parlange, M. B.: A New Wall Shear Stress Model for Atmospheric Boundary Layer Simulations, J. Atmos. Sci., 70, 3460–3470, https://doi.org/10.1175/JAS-D-12-0257.1, 2013. a
Huq, S., De Roo, F., Raasch, S., and Mauder, M.: Vertically nested LES for high-resolution simulation of the surface layer in PALM (version 5.0), Geosci. Model Dev., 12, 2523–2538, https://doi.org/10.5194/gmd-12-2523-2019, 2019. a
Institut Wohnen und Umwelt (IWU): Deutsche Gebäudetypologie – Systematik und Datensätze, periodically updated, available at: https://www.iwu.de/fileadmin/user_upload/dateien/energie/klima_altbau/Gebaeudetypologie_Deutschland.pdf (last access: April 2019), 2005 (in German). a
Jarvis, P. G.: The interpretation of the variations in leaf water p.otential and stomatal conductance found in canopies in the field, Philos. Trans. Roy. Soc. London, 273B, 593–610, 1976. a
Jendritzky, G., de Dear, R., and Havenith, G.: UTCI – Why another thermal index?, Int. J. Biometeorol., 56, 421–428, 2012. a
Jöckel, P., Kerkweg, A., Pozzer, A., Sander, R., Tost, H., Riede, H., Baumgaertner, A., Gromov, S., and Kern, B.: Development cycle 2 of the Modular Earth Submodel System (MESSy2), Geosci. Model Dev., 3, 717–752, https://doi.org/10.5194/gmd-3-717-2010, 2010. a
Jonkman, J. M., Butterfield, S., Musial, W., and Scott, G.: Definition of a 5-MW reference wind turbine for offshore system development, Technical Report NREL/TP-500-38060, National Renewable Energy Laboratory, Golden, CO, 2009. a, b, c
Kanda, M., Inagaki, A., Letzel, M. O., Raasch, S., and Watanabe, T.: LES study of the energy imbalance problem with eddy covariance fluxes, Bound.-Lay. Meteorol., 110, 381–404, 2004. a
Karamouzas, I., Skinner, B., and Guy, S. J.: Universal Power Law Governing Pedestrian Interactions, Phys. Rev. Lett., 113, 238701, https://doi.org/10.1103/PhysRevLett.113.238701, 2014. a, b
Kataoka, H. and Mizuno, M.: Numerical flow computation around aerolastic 3d square cylinder using inflow turbulence, Wind Struct., 5, 379–392, 2002. a
Khairoutdinov, M. and Kogan, Y.: A new cloud physics parameterization in a large-eddy simulation model of marine stratocumulus, Mon. Weather Rev., 128, 229–243, 2000. a
Khvorostyanov, V. I. and Curry, J. A.: Aerosol size spectra and CCN activity spectra: Reconciling the lognormal, algebraic, and power laws, J. Geophys. Res.-Atmos., 111, D12202, https://doi.org/10.1029/2005JD006532, 2006. a
Kim, Y., Castro, I. P., and Xie, Z.-T.: Divergence-free turbulence inflow conditions for large-eddy simulations with incompressible flow solvers, Comput. Fluids, 84, 56–68, https://doi.org/10.1016/j.compfluid.2013.06.001, 2013. a
Kokkola, H., Korhonen, H., Lehtinen, K. E. J., Makkonen, R., Asmi, A., Järvenoja, S., Anttila, T., Partanen, A.-I., Kulmala, M., Järvinen, H., Laaksonen, A., and Kerminen, V.-M.: SALSA – a Sectional Aerosol module for Large Scale Applications, Atmos. Chem. Phys., 8, 2469–2483, https://doi.org/10.5194/acp-8-2469-2008, 2008. a
Krayenhoff, E. S. and Voogt, J. A.: A microscale three-dimensional urban energy balance model for studying surface temperatures, Bound.-Lay.. Meteorol., 123, 433–461, https://doi.org/10.1007/s10546-006-9153-6, 2007. a
Kurppa, M., Hellsten, A., Roldin, P., Kokkola, H., Tonttila, J., Auvinen, M., Kent, C., Kumar, P., Maronga, B., and Järvi, L.: Implementation of the sectional aerosol module SALSA2.0 into the PALM model system 6.0: model development and first evaluation, Geosci. Model Dev., 12, 1403–1422, https://doi.org/10.5194/gmd-12-1403-2019, 2019. a, b
Launder, B. and Spalding, D.-B.: The numerical computation of turbulent flow, Comput. Method. Appl. M., 3, 269–289, 1974. a
Letzel, M. O., Helmke, C., Ng, E., An, X., Lai, A., and Raasch, S.: LES case study on pedestrian level ventilation in two neighbourhoods in Hong Kong, Meteorol. Z., 21, 575–589, 2012. a
Lo, K. W. and Ngan, K.: Characterizing Ventilation and Exposure in Street Canyons Using Lagrangian Particles, J. Appl. Meteorol. Climatol., 56, 1177–1194, https://doi.org/10.1175/JAMC-D-16-0168.1, 2017. a
Lund, T. S., Wu, X., and Squires, K. D.: Generation of turbulent inflow data for spatially-developing boundary layer simulations, J. Comp. Phys., 140, 233–258, 1998. a, b
Maronga, B.: Monin-Obukhov similarity functions for the structure parameters of temperature and humidity in the unstable surface layer: Results from high-resolution large-eddy simulations, J. Atmos. Sci., 71, 716–733, 2014. a
Maronga, B.: PALM 6.0 r3668, https://doi.org/10.25835/0041607, 2019. a
Maronga, B. and Bosveld, F. C.: Key parameters for the life cycle of nocturnal radiation fog: a comprehensive large-eddy simulation study, Q. J. Roy. Meteor. Soc., 143, 2463–2480, https://doi.org/10.1002/qj.3100, 2017. a
Maronga, B. and Raasch, S.: Large-eddy simulations of surface heterogeneity effects on the convective boundary layer during the LITFASS-2003 experiment, Bound.-Lay. Meteorol., 146, 17–44, 2013. a
Maronga, B. and Reuder, J.: On the formulation and universality of Monin-Obukhov similarity functions for mean gradients and standard deviations in the unstable surface layer: results from surface-layer resolving large-eddy simulations, J. Atmos. Sci., 74, 989–1010, https://doi.org/10.1175/JAS-D-16-0186.1, 2017. a, b, c, d
Maronga, B., Hartogensis, O. K., Raasch, S., and Beyrich, F.: The effect of surface heterogeneity on the structure parameters of temperature and specific humidity: A large-eddy simulation case study for the LITFASS-2003 experiment, Bound.-Lay. Meteorol., 153, 441–470, 2014. a
Maronga, B., Gryschka, M., Heinze, R., Hoffmann, F., Kanani-Sühring, F., Keck, M., Ketelsen, K., Letzel, M. O., Sühring, M., and Raasch, S.: The Parallelized Large-Eddy Simulation Model (PALM) version 4.0 for atmospheric and oceanic flows: model formulation, recent developments, and future perspectives, Geosci. Model Dev., 8, 2515–2551, https://doi.org/10.5194/gmd-8-2515-2015, 2015. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Maronga, B., Gross, G., Raasch, S., Banzhaf, S., Forkel, R., Heldens, W., Kanani-Sühring, F., Matzarakis, A., Mauder, M., Pavlik, D., Pfafferott, J., Schubert, S., Seckmeyer, G., Sieker, H., and Winderlich, K.: Development of a new urban climate model based on the model PALM - Project overview, planned work, and first achievements, Meteorol. Z., 28, 105–119, 2019. a, b
Maronga, B., Knigge, C., and Raasch, S.: An Improved Surface Boundary Condition for Large-Eddy Simulations Based on Monin-Obukhov Similarity Theory: Evaluation and Consequences for Grid Convergence in Neutral and Stable Conditions, Bound.-Lay. Meteorol., 174, 297–325, https://doi.org/10.1007/s10546-019-00485-w, in press, 2020. a
Mason, P. J. and Sykes, R. I.: A simple cartesian model of boundary layer flow over topography, J. Comp. Phys., 28, 198–210, 1978. a
Mayer, B. and Kylling, A.: Technical note: The libRadtran software package for radiative transfer calculations – description and examples of use, Atmos. Chem. Phys., 5, 1855–1877, https://doi.org/10.5194/acp-5-1855-2005, 2005. a
McWilliams, J. C., Sullivan, P. P., and Moeng, C.-H.: Langmuir turbulence in the ocean, J. Fluid Mech., 334, 1–30, 1997. a
Mellor, G. L. and Yamada, T.: A hierarchy of turbulence closure models for planetary boundary layers, J. Atmos. Sci., 31, 1791–1806, https://doi.org/10.1175/1520-0469(1974)031<1791:AHOTCM>2.0.CO;2, 1974. a
Mellor, G. L. and Yamada, T.: Development of a turbulence closure model for geophysical fluid problems, Rev. Geophys., 20, 851–875, 1982. a
Moeng, C.-H. and Wyngaard, J. C.: Spectral analysis of large-eddy simulations of the convective boundary layer, J. Atmos. Sci., 45, 3573–3587, 1988. a
Mokhtarpoor, R. and Heinz, S.: Dynamic large eddy simulation: Stability via realizability, Phys. Fluids, 29, 105104, https://doi.org/10.1063/1.4986890, 2017. a, b
Noh, Y., Min, H. S., and Raasch, S.: Large eddy simulation of the ocean mixed layer: The effects of wave breaking and Langmuir circulation, J. Phys. Oceanogr., 34, 720–735, 2004. a, b
Noh, Y., Oh, D., Hoffmann, F., and Raasch, S.: A Cloud Microphysics Parameterization for Shallow Cumulus Clouds Based on Lagrangian Cloud Model Simulations, J. Atmos. Sci., 75, 4031–4047, 2018. a
Oliveira, P. J. and Younis, B. A.: On the prediction of turbulent flows around full-scale buildings, J. Wind Eng. Ind. Aerod., 86, 203–220, https://doi.org/10.1016/s0167-6105(00)00011-8, 2000. a
Orlanski, I.: A simple boundary condition for unbounded hyperbolic flows, J. Comput. Phys., 21, 251–269, 1976. a
Panofsky, H. A. and Dutton, J. A.: Atmospheric turbulence, models and methods for engineering applications, John Wiley & Sons, New York, 1984. a, b
Paulson, C. A.: The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer, J. Appl. Meteorol., 9, 857–861, 1970. a
Pfafferott, J., Fischer, M., Strohmeyer, T., and Wirth, D.: Ein einfaches Modell zur Vorhersage der Fassaden- und Grenzschichttemperatur, BAUPHYSIK, 33, 151–157, 2011 (in German). a
Raasch, S. and Franke, T.: Structure and formation of dust-devil-like vortices in the atmospheric boundary layer – A high resolution numerical study, J. Geophys. Res., 116, D16120, https://doi.org/10.1029/2011JD016010, 2011. a
Resler, J., Krč, P., Belda, M., Juruš, P., Benešová, N., Lopata, J., Vlček, O., Damašková, D., Eben, K., Derbek, P., Maronga, B., and Kanani-Sühring, F.: PALM-USM v1.0: A new urban surface model integrated into the PALM large-eddy simulation model, Geosci. Model Dev., 10, 3635–3659, https://doi.org/10.5194/gmd-10-3635-2017, 2017. a, b, c, d, e
Riechelmann, T., Noh, Y., and Raasch, S.: A new method for large-eddy simulations of clouds with Lagrangian droplets including the effects of turbulent collision, New J. Phys., 14, 065008, https://doi.org/10.1088/1367-2630/14/6/065008, 2012. a, b, c, d
Rotach, M. W., Gryning, S.-E., and Tassone, C.: A two-dimensional Lagrangian stochastic dispersion model for daytime conditions, Q. J. Roy. Meteor. Soc., 122, 367–389, https://doi.org/10.1002/qj.49712253004, 1996. a, b
Saiki, E. M., Moeng, C.-H., and Sullivan, P. P.: Large-eddy simulation of the stably stratified planetary boundary layer, Bound. Lay.-Meteorol., 95, 1–30, 2000. a
Saunders, S. M., Jenkin, M. E., Derwent, R. G., and Pilling, M. J.: Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part A): tropospheric degradation of non-aromatic volatile organic compounds, Atmos. Chem. Phys., 3, 161–180, https://doi.org/10.5194/acp-3-161-2003, 2003. a
Scherer, D., Ament, F., Emeis, S., Fehrenbach, U., Leitl, B., Scherber, K., Schneider, C., and Vogt, U.: Three-Dimensional Observation of Atmospheric Processes in Cities, Meteorol. Z., 28, 121–138, https://doi.org/10.1127/metz/2019/0911, 2019a. a
Scherer, D., Antretter, F., Bender, S., Cortekar, J., Emeis, S., Fehrenbach, U., Gross, G., Halbig, G., Hasse, J., Maronga, B., Raasch, S., and Scherber, K.: Urban Climate Under Change [UC]2 – A national research programme for developing a building-resolving atmospheric model for entire city regions, Meteorol. Z., 28, 95–104, https://doi.org/10.1127/metz/2019/0913, 2019b. a, b
Schrempf, M., Thuns, N., Lange, K., and Seckmeyer, G.: Impact of Orientation on the Vitamin D Weighted Exposure of a Human in an Urban Environment, Int. J. Env. Res. Pub. He., 14, 920, https://doi.org/10.3390/ijerph14080920, 2017. a
Schroeder, W., Martin, K., and Lorensen, B.: Visualization Toolkit: An Object-Oriented Approach to 3D Graphics, 4th Edition, Kitware, 2006. a
Schumann, U.: Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli, J. Comput. Phys., 18, 376–404, 1975. a
Schwenkel, J. and Maronga, B.: Large-eddy simulation of radiation fog with comprehensive two-moment bulk microphysics: impact of different aerosol activation and condensation parameterizations, Atmos. Chem. Phys., 19, 7165–7181, https://doi.org/10.5194/acp-19-7165-2019, 2019. a
Schwenkel, J., Hoffmann, F., and Raasch, S.: Improving collisional growth in Lagrangian cloud models: development and verification of a new splitting algorithm, Geosci. Model Dev., 11, 3929–3944, https://doi.org/10.5194/gmd-11-3929-2018, 2018. a, b
Seckmeyer, G., Schrempf, M., Wieczorek, A., Riechelmann, S., Graw, K., Seckmeyer, S., and Zankl, M.: A Novel Method to Calculate Solar UV Exposure Relevant to Vitamin D Production in Humans, Photochem. Photobiol., 89, 974–983, 2013. a
Seifert, A. and Beheng, K. D.: A double-moment parameterization for simulating autoconversion, accretion and selfcollection, Atmos. Res., 59, 265–281, 2001. a
Seifert, A. and Beheng, K. D.: A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 1: Model description, Meteorol. Atmos Phys., 92, 45–66, 2006. a
Shima, S.-I., Kusano, K., Kawano, A., Sugiyama, T., and Kawahara, S.: The super-droplet method for the numerical simulation of clouds and precipitation: A particle-based and probabilistic microphysics model coupled with a non-hydrostatic model, Q. J. Roy. Meteor. Soc., 135, 1307–1320, 2009. a, b, c
Skyllingstad, E. D. and Denbo, D. W.: An ocean large-eddy simulation of Langmuir circulations and convection in the surface mixed layer, J Geophys. Res., 100, 8501–8522, 1995. a
Sölch, I. and Kärcher, B.: A large-eddy model for cirrus clouds with explicit aerosol and ice microphysics and Lagrangian ice particle tracking, Q. J. Roy. Meteor. Soc., 136, 2074–2093, 2010. a
Staiger, H., Laschewski, G., and Graetz, A.: The perceived temperature – a versatile index for the assessment of the human thermal environment. Part A: scientific basics, Int. J. Biometeorol., 56, 165–176, https://doi.org/10.1007/s00484-011-0409-6, 2012. a
Staiger, H., Laschewski, G., and Matzarakis, A.: Selection of Appropriate Thermal Indices for Applications in Human Biometeorological Studies, Atmosphere, 10, 1–15, 2019. a
Steinfeld, G., Raasch, S., and Markkanen, T.: Footprints in homogeneously and heterogeneously driven boundary layers derived from a Lagrangian stochastic particle model embedded into large-eddy simulation, Bound.-Lay. Meteorol, 129, 225–248, 2008. a
Stewart, J. B.: Modelling surface conductance of pine forest, Agr. Forest Meteorol., 43, 19–35, 1988. a, b
Storey, R., Norris, S., and Cater, J.: Large Eddy Simulation of Wind Events Propagating through an Array of Wind Turbines, in: Proceedings of the World Congress on Engineering 2013, Vol. III, WCE 2013, London, UK, 3–5 July, 2013. a
Sühring, M. and Raasch, S.: Heterogeneity-induced heat flux patterns in the convective boundary layer: Can they be detected from observations and is there a blending height? - A large-eddy simulation study for the LITFASS-2003 experiment, Bound.-Lay. Meteorol., 148, 309–331, 2013. a
Sühring, M., Metzger, S., Xu, K., Durden, D., and Desai, A.: Trade-Offs in Flux Disaggregation: A Large-Eddy Simulation Study, Bound.-Lay. Meteorol., 170, 69–93, https://doi.org/10.1007/s10546-018-0387-x, 2019. a
Sullivan, P. P. and Patton, E. G.: The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation, J. Atmos. Sci., 68, 2395–2415, 2011. a
Sullivan, P. P., McWilliams, J. C., and Moeng, C.-H.: A grid nesting method for large-eddy simulation of planetary boundary-layer flow, Bound.-Lay. Meteorol., 80, 167–202, 1996. a
Sullivan, P. P., Weil, J. C., Patton, E. G., Jonker, H. J. J., and Mironov, D. V.: Turbulent Winds and Temperature Fronts in Large-Eddy Simulations of the Stable Atmospheric Boundary Layer, J. Atmos. Sci., 73, 1815–1840, https://doi.org/10.1175/JAS-D-15-0339.1, 2016. a
Twomey, S.: The nuclei of natural cloud formation part II: The supersaturation in natural clouds and the variation of cloud droplet concentration, Pure Appl. Geophys., 43, 243–249, 1959. a
Unterstrasser, S. and Sölch, I.: Optimisation of the simulation particle number in a Lagrangian ice microphysical model, Geosci. Model Dev., 7, 695–709, https://doi.org/10.5194/gmd-7-695-2014, 2014. a
Unterstrasser, S., Hoffmann, F., and Lerch, M.: Collection/aggregation algorithms in Lagrangian cloud microphysical models: rigorous evaluation in box model simulations, Geosci. Model Dev., 10, 1521–1548, https://doi.org/10.5194/gmd-10-1521-2017, 2017. a, b
Valentin, J.: Basic anatomical and physiological data for use in radiological protection: reference values: ICRP Publication 89, Annals of the ICRP, 32, 1–277, https://doi.org/10.1016/S0146-6453(03)00002-2, 2002. a
van Genuchten, M.: A closed form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Amer. J., 44, 892–898, 1980. a
Van Zanten, M. C., Sauter, F. J., Kruit, R. J. W., Jaarsveld, J. A. V., and Pul, W. A. J. V.: Description of the DEPAC module: Dry deposition modelling with DEPAC-GCN2010, Tech. report 680180001/2010, RIVM, Bilthoven, the Netherlands, 74 pp., 2010. a
Viterbo, P. and Beljaars, A. C. M.: An Improved Land Surface Parameterization Scheme in the ECMWF Model and Its Validation, J. Climate, 8, 2716–2748, 1995. a
Vollmer, L., Steinfeld, G., Heinemann, D., and Kühn, M.: Estimating the wake deflection downstream of a wind turbine in different atmospheric stabilities: an LES study, Wind Energ. Sci., 1, 129–141, https://doi.org/10.5194/wes-1-129-2016, 2016. a, b
Vollmer, L., Steinfeld, G., and Kühn, M.: Transient LES of an offshore wind turbine, Wind Energ. Sci., 2, 603–614, https://doi.org/10.5194/wes-2-603-2017, 2017. a
Voss, K. and Künz, C.: Klimadaten und Klimawandel – Untersuchungen zum Einfluss auf den Energiebedarf, den Leistungsbedarf und den thermischen Komfort von Gebäuden, Bauphysik, 34, 189–196, 2012 (in German). a
Weil, J. C., Sullivan, P. P., and Moeng, C.-H.: The use of large-eddy simulations in Lagrangian particle dispersion models, J. Atmos. Sci., 61, 2877–288, 2004. a, b
Wu, Y.-T. and Porté-Agel, F.: Large-Eddy Simulation of Wind-Turbine Wakes: Evaluation of Turbine Parametrisations, Bound.-Lay. Meteorol., 138, 345–366, https://doi.org/10.1007/s10546-010-9569-x, 2011. a
Xie, Z.-T. and Castro, I. P.: LES and RANS for turbulent flows over arrays of wall-mounted obstacles, Flow Turbul. Combust., 76, 291–312, 2006. a
Xie, Z.-T. and Castro, I. P.: Efficient Generation of Inflow Conditions for Large Eddy Simulation of Street-Scale Flows, Flow Turbul. Combust., 81, 449–470, https://doi.org/10.1007/s10494-008-9151-5, 2008. a, b
Zhang, L., Gong, S., Padro, J., and Barrie, L.: A size-segregated particle dry deposition scheme for an atmospheric aerosol module, Atmos. Environ., 39, 3291–3303, 2001. a
Available as download from http://palm-model.org (last access: 18 February 2020)
See https://ferret.pmel.noaa.gov/Ferret/documentation/coards-netcdf-conventions, last access: 18 February 2020.
- Abstract
- Introduction
- PALM model core
- Embedded models
- PALM-4U components
- Technical details
- Summary and future developments
- Appendix A: List of frequently used abbreviations
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- PALM model core
- Embedded models
- PALM-4U components
- Technical details
- Summary and future developments
- Appendix A: List of frequently used abbreviations
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References