the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An urban trees parameterization for modeling microclimatic variables and thermal comfort conditions at street level with the Town Energy Balance model (TEB-SURFEX v8.0)
Emilie Redon
Aude Lemonsu
Valéry Masson
The Town Energy Balance (TEB) urban climate model has recently been improved to more realistically address the radiative effects of trees within the urban canopy. These processes necessarily have an impact on the energy balance that needs to be taken into account. This is why a new method for calculating the turbulent fluxes for sensible and latent heat has been implemented. This method remains consistent with the “bigleaf” approach of the Interaction Soil–Biosphere–Atmosphere (ISBA) model, which deals with energy exchanges between vegetation and atmosphere within TEB. Nonetheless, the turbulent fluxes can now be dissociated between ground-based natural covers and the tree stratum above (knowing the vertical leaf density profile), which can modify the vertical profile in air temperature and humidity in the urban canopy. In addition, the aeraulic effect of trees is added, parameterized as a drag term and an energy dissipation term in the evolution equations of momentum and turbulent kinetic energy, respectively. This set of modifications relating to the explicit representation of the tree stratum in TEB is evaluated on an experimental case study. The model results are compared to micrometeorological and surface temperature measurements collected in a semi-open courtyard with trees and bordered by buildings. The new parameterizations improve the modeling of surface temperatures of walls and pavements, thanks to taking into account radiation absorption by trees, and of air temperature. The effect of wind speed being strongly slowed down by trees is also much more realistic. The universal thermal climate index diagnosed in TEB from inside-canyon environmental variables is highly dependent and sensitive to these variations in wind speed and radiation. This demonstrates the importance of properly modeling interactions between buildings and trees in urban environments, especially for climate-sensitive design issues.
- Article
(884 KB) -
Supplement
(6224 KB) - BibTeX
- EndNote
The urban climate commonly refers to the modification of local climate by the urban environment. It results from the establishment of radiative, energetic, dynamic, and hydrological surface processes that are peculiar to urban cover properties (Oke et al., 2017). This urban climate may, however, present important spatial variabilities within the city. The street-level meteorological variables, i.e., air temperature, humidity, and wind, are modified by the local environment depending on the morphology and arrangement of buildings, the surface properties, and more generally the land cover composition (Houet and Pigeon, 2011; Fenner et al., 2014; Ndetto and Matzarakis, 2014; Alexander and Mills, 2014).
The presence of vegetation, and especially urban trees, is one element of local microclimate change (Bernatzky, 1982; Oke, 1989; Shashua-Bar and Hoffman, 2000; Potchter et al., 2006; Shashua-Bar et al., 2011). The trees functioning is governed by specific physiological processes together with local environmental conditions. When located in a street canyon, the trees interact with the surrounding urban elements. The radiative exchanges are modified, as well as the energy fluxes and local airflows. The incoming radiation is intercepted by the tree foliage depending on its localization and coverage in the street (Souch, 1993; Armson et al., 2012; Berry et al., 2013). It is partly reflected upward according to the reflective properties of leaves, whereas the other part is partially transmitted through the foliage or absorbed by it. Scattering modulates the properties of reflected and transmitted radiation. Multiple reflections of short- and long-wave radiation between all components of the canyon are also disrupted by the presence of trees that are furthermore an additional source of infrared emissions. A part of the energy absorbed by trees is used in the transpiration process associated with photosynthesis (Peters et al., 2011; Qiu et al., 2013). This is a water exchange from aerial parts of plants to the atmosphere through stomata. The transpiration rate is related to the stomata opening level, which is regulated according to the environmental conditions of sunlight, temperature, humidity, and wind, but also to soil water availability (Konarska et al., 2016; Litvak and Pataki, 2016). As a consequence, the energy exchanges that are mostly dominated by heat transfers through conduction and convection in built-up environments can be significantly modified with the vegetation effects (Grimmond et al., 1996; Offerle et al., 2006; Best and Grimmond, 2016). Finally, the trees are physical obstacles to the airflow within the street (Heisler, 1990; Giometto et al., 2017; Martini et al., 2017). They produce a drag effect on the mean flow and modify local turbulent exchanges, which can have an impact on ventilation as well as on particle dispersion (Buccolieri et al., 2011; Abhijith et al., 2017).
Some urban climate models are capable of simulating the presence of certain vegetated elements in the urban environment. However, they are not represented with the same level of accuracy, nor the same physical processes. The high spatial resolution software or numerical models that are based on near-reality numerical mock-ups of the environment integrate natural soils and trees as full elements composing the scene. Trees can be spatially arranged and are described by a set of voxels to represent the shape of the crowns, while the trunks are mostly neglected. These fine scales are suitable for studying the airflow and dispersion processes in the street using computational fluid dynamics (CFD) models. In this configuration, trees are positioned as porous obstacles (Bruse and Fleer, 1998; Salim et al., 2015) that slow down and modify the flow. For models such as SOLENE (Miguet and Groleau, 2007), DART (Gastellu-Etchegorry et al., 1996), or SOLWEIG (Lindberg and Grimmond, 2011), mainly dedicated to radiative transfer, trees are resolved explicitly and described as turbid objects that intercept, transmit, absorb, and emit radiation in complex interactions between all surrounding objects of the scene. The dynamic effects and energy exchanges associated with vegetation are not addressed, in particular soil evaporation and plant transpiration. This is the case with the models LASER/F (Kastendeuch et al., 2017; Bournez, 2018), SOLENE-microclimate (Bouyer et al., 2011; Malys et al., 2014, extension of the SOLENE radiative model), or ENVI-met (Bruse and Fleer, 1998; Bruse, 2004) that take into account a set of radiative, energetic, hydrological, and dynamic processes, allowing a better description of the complex interactions within the urban canopy layer. ENVI-met probably represents the most advanced and complete model. It distinguishes between buildings, artificial and natural ground surfaces, tree vegetation, and air. For natural elements, it computes radiative exchanges by considering radiation absorption coefficients by vegetation according to the leaf area density profile. It also integrates a vegetation model for the calculation of water and energy exchanges including the sensible heat flux between foliage and air, the evaporation of water intercepted by foliage, and the transpiration of plants controlled by a stomatal resistance. This vegetation scheme is associated with a soil model to calculate the evolution of water content and thus to modulate the evaporation capacity of plants depending on water availability.
These models are dedicated to urban microclimate modeling from street to neighborhood scales. They address needs for climate-sensitive design issues and assessment of environmental conditions within the urban canopy layer, but they are not suitable for studying interactions with local meteorology and mesoscale processes. Coupling to mesoscale models (or even climate models) requires the use of less time-consuming urban canopy models based on a simplified and parameterized description of the urban environment and processes involved. Some of them now include a representation of urban vegetation (Lemonsu et al., 2012; Wang et al., 2013) and even of trees (Lee and Park, 2008; Krayenhoff et al., 2014; Ryu et al., 2016; Redon et al., 2017). Lee and Park (2008) and Lee (2011) were the first to address tree effects in urban canyons in their Vegetated Urban Canopy Model (VUCM). Although it is a single-layer model with a somewhat simplistic description of trees and parameterization of associated radiative effects, this model has the advantage of also considering the energetic, hydrological, and aeraulic processes. At the foliage level, it calculates temperature evolution, heat turbulent exchanges, surface water evaporation, and transpiration. It also calculates for the natural soil compartment the water fluxes and the root water uptake related to transpiration. Finally, the formulation of the mean horizontal wind speed at street level includes the drag effect of trees. Ryu et al. (2016) also offer a very complete modeling of the physical processes. The description of trees is more refined (two rows of symmetrical trees with circular crowns), particularly for the radiative exchanges and calculation of the form factors with Monte Carlo simulations. Finally, BEP-Tree is the first multilayer urban canopy model which includes both radiative properties (Krayenhoff et al., 2014) and aeraulic effects (Krayenhoff et al., 2015) of trees. The foliage layer can occupy part of the canyon and extends above rooftops. It interacts directly with the first levels of the atmospheric model from a dynamic point of view. However, the model does not address the heat and water fluxes of vegetation and their potential impact on microclimatic variables.
The TEB model, which is part of the urban canopy models for mesoscale applications, is presented in the next section. It offers the interesting ability of being able to be applied over the whole city and to operate in complete three-dimensional atmospheric simulations where two-way interactions between complex surfaces and atmosphere are resolved. It has then the capability to simulate a certain level of microclimate variability between neighborhoods (de Munck et al., 2018), especially according to the presence of vegetation and trees and the potential influences or interferences between local microclimates by horizontal advection. The objective here is to propose a refinement of the already existing parameterization of urban vegetation and more specifically of energetic and aeraulic effects of trees.
2.1 Previous developments and general approach
The Town Energy Balance (TEB) urban canopy model is one of the first models from this generation to have included urban vegetation in local-scale interactions with the built-up elements. It has been progressively made more complex by integrating new types of natural elements and new associated processes. The first step was the inclusion of ground-based vegetation within the canyon by implementing the Interaction Soil–Biosphere–Atmosphere (ISBA, Noilhan and Planton, 1989) model within TEB (Lemonsu et al., 2012). ISBA is a surface–vegetation–atmosphere transfer (SVAT) model. This coupling makes it possible to simulate the physiological behavior of plants subject to radiative effects of urban geometry and to microclimate conditions of the urban environment. Reversely, the microclimate within the canyon can be impacted by the modification of surface energy exchanges due to the presence of vegetation at the ground, especially by its evapotranspiration. A module of extensive green roofs was also developed (de Munck et al., 2013) still using the ISBA model to simulate the hydrological and energetic functioning of the green roofs, as well as the energy exchanges with atmosphere and the thermal coupling with the buildings on which they are installed.
2.2 Radiative effects of urban trees
Finally, the most recent developments are related to trees. Redon et al. (2017) proposed a new parameterization for modeling the radiative effects of trees by including a tree-foliage stratum within the urban canyon which can partially cover ground-based surfaces. The positioning and geometry of individual trees are not described explicitly but rather approached as (1) a horizontal coverage fraction within the canyon, (2) a vertical thickness by defining a mean height of trees and a mean height of trunks, and (3) a mean leaf density profile (see description in Fig. 1). The tree foliage can intercept a part of incoming radiation depending on canyon geometry, which is either reflected upward or transmitted through the foliage, or absorbed by the foliage. In addition, the foliage layer takes part in radiation inter-reflections within the canyon between the different components (trees, walls, road, ground-based natural covers) and contributes to infrared emissions. Separated calculations are done for direct and diffuse components of short-wave radiation and for long-wave radiation. The direct short-wave radiation is assumed directional, whereas the diffuse short-wave radiation, the long-wave radiation, and any radiation after reflection are assumed to be isotropic. The radiation interactions between all components of the canyon are consequently managed using form factors calculated between all of them.
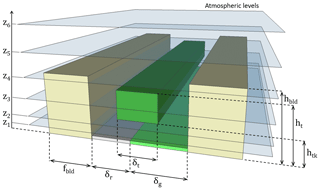
Figure 1Schematic representation of the TEB urban canyon, integrating a part of ground-based natural covers and an explicit tree-foliage layer, and of the atmospheric vertical levels of the surface boundary layer (SBL) scheme coupled to TEB to compute vertical profiles of micrometeorological variables inside and above the canyon.
These developments were evaluated by comparison with solar enlightenment modeling performed by a high-resolution architectural software for a large set of simple-geometry urban canyons, with various aspect ratios and various tree arrangements within (Redon et al., 2017). Due to the simplified representation of tree geometry, a general defect is the underestimation of the incoming solar radiation interception by the tree-foliage stratum. That is explained by the fact that TEB does not represent the sides of tree crowns, which can receive in reality a part of incoming radiation according to their position and the inclination of the sun's rays. The simplified approach is also a limitation for describing some vegetation arrangements such as multiple lanes of trees. Nonetheless, the results are quite acceptable and confirm that this new version makes it possible to better simulate the radiative interactions in canyons with trees.
In coherence with this explicit separation of vegetation strata, there was then a need to adapt the calculation of the turbulent fluxes related to low and high vegetation, as well as to include the drag effect of trees on wind profile in the canyon. These new developments and their evaluation by comparison to microclimatic measurements are presented and discussed here. They are complemented by an updated calculation of the universal thermal comfort index (UTCI) by including the effect of trees.
3.1 Description of natural covers with the “bigleaf” approach
The TEB model resolves the radiative budget for each component of the urban canyon. In the case of a treeless canyon, it accounts for obstruction effects due to buildings in the calculation of incoming short- and long-wave radiation interception by roads, walls, and natural ground-based surfaces, as described in detail in Masson (2000) and Lemonsu et al. (2012). The new version by Redon et al. (2017) now includes the additional interactions with the tree-foliage stratum. From the resolution of the radiation budget, the energy quantity absorbed in short- (S*) and long-wave (L*) radiation by each component or net radiation (Q*) is determined:
This net energy source is redistributed as turbulent sensible (QH) and latent (QE) heat fluxes, between each considered component and local atmosphere, and as a storage heat flux by conduction (QG) through the component itself (i.e., through the artificial-material layers that compose the roof, the road, the walls, or the ground for natural covers).
For the built-up facets of the urban canyon (road, wall, roof), the surface energy balance (SEB) calculations remain unchanged in the TEB model but with Q* potentially modified in the case of canyons with trees. Since the works of Lemonsu et al. (2012), the turbulent processes for natural parts of the urban canyon (natural soils and ground-based vegetation) are resolved in TEB through the integration of the ISBA model that is here constrained by radiative and microclimatic conditions related to the urban environment. The ISBA model is based on what is called the bigleaf approach in which the natural covers are managed as a unique composite compartment. This compartment consists of fractions of bare soil, low vegetation, and high vegetation (and possibly snow). It is characterized by mean properties calculated from thermoradiative (albedo, emissivity, heat capacity), aerodynamic (roughness length), and physiological (stomatal resistance for plants) parameters that are prescribed independently for the different types that compose it. A single temperature (Tnat) is associated with the compartment, and a single SEB is resolved:
This net radiation depends on the radiation budget, which is expressed as the following:
The incoming short- and long-wave radiation intercepted by the natural cover compartment ( and ) is calculated for a reference level at the ground within the urban canyon. The composite albedo (αnat) is calculated as an average of bare soil and vegetation albedos (which are themselves average albedos of snow-covered and snow-free surfaces). The same is done for the emissivity (ϵnat).
3.2 Modification of surface energy balance due to implementation of trees
The implementation of a tree canopy in TEB, like a supplementary foliage stratum, makes it possible to separate the incoming radiation received by natural covers as a part received by ground-based natural surfaces ( and ) and a part received by trees ( and ) and also to compute the net radiation for both of them ( and ). For simplicity, the bigleaf concept used in ISBA for the SEB calculation and the resolution of the surface-layer temperature evolution equation is here retained. This requires us to calculate aggregated radiation fluxes intercepted by the compartment of natural covers, which must be provided to ISBA. Considering that the foliage stratum partially overlaps the ground-based surfaces, these fluxes are aggregated according to the cumulative fraction of natural covers and by accounting for the distribution between covers at the ground and trees:
Here, δg is the ground-based surface fraction of the canyon covered by gardens (i.e., bare soil and low vegetation) and δt is the overlapping fraction of tree stratum. Note that these fractions are not dependant on one another so that their sum can be greater than 1 (Fig. 1). Both and fluxes calculated by ISBA for the composite compartment (Lemonsu et al., 2012) are then simply redistributed in two contributions from ground-based natural covers ( and ) and from trees ( and ) to ensure the energy conservation:
4.1 Principle of the surface boundary layer parameterization
The TEB-SBL (SBL refers to the surface boundary layer) parameterization has been implemented in TEB in order to improve the meteorological variable prediction within the urban canyon (Hamdi and Masson, 2008; Masson and Seity, 2009; Lemonsu et al., 2012). TEB-SBL resolves the surface boundary layer for an air volume in the canyon from a system of evolution equations for air temperature (T), specific humidity (q), wind speed (U), and turbulent kinetic energy (E). For taking into account the effects of canyon on the evolution of local atmospheric characteristics, an additional forcing term is included in each of these equations, according to the approach proposed by Yamada (1982) for the drag forces related to the vegetation canopies. The equations have the same general expression, with V the considered variable and FV the general forcing term including advection, Coriolis force, and pressure gradient:
The last term to the right is the forcing term due to the canyon. It translates a drag force for the wind, a heating/cooling effect for air temperature, a humidification/dryness effect for air humidity, and a dissipation/production effect for turbulent kinetic energy. According to Martilli et al. (2002), these additional contributions are associated with horizontal (H) and vertical (V) surfaces of the canyon:
For these terms, the equations are resolved according to a vertical discretization of the air volume from the ground to a reference atmospheric level located above the top of buildings (Fig. 1). As described by Lemonsu et al. (2012), the equation system of the TEB-SBL parameterization is expressed as the following for each k vertical layer:
where is the drag coefficient for buildings, u* the friction velocity at level k, Vair the air volume of the SBL-scheme layer where exchanges take place, ρ is the air density, and ℒv is the latent heat for vaporization. The sensible heat fluxes of vertical surfaces ( for walls) contribute to air temperature evolution at layer k relative to the fraction of the total wall surface in contact with the considered air layer (). The sensible heat fluxes of horizontal surfaces combine , , and for roofs, road, and natural covers, respectively. The roofs only contribute to air temperature for vertical levels above building tops (with surface ). The contributions of road and of natural covers are here included at the ground level so that they affect only the first layer of TEB-SBL (with respective surfaces and ). The same types of contributions are parameterized for humidity but in the form of latent heat fluxes.
The vertical transport of heat, humidity, and momentum within and above the canyon is calculated by applying the turbulence scheme by Cuxart et al. (2000). This scheme is based on an equation for the turbulent kinetic energy, and it is closed with a mixing length. This is parameterized in TEB on the basis of the work by Santiago and Martilli (2010) according to the height of buildings, the mean frontal area density, and the displacement height, i.e., parameters depending on the geometry of the canyon (see Eqs. 10–12 in Lemonsu et al., 2012).
4.2 Distribution of heat and humidity fluxes from natural covers
The implementation of trees in TEB requires us to modify the ensemble of equations in order to take into account the vertical redistribution of turbulent fluxes and the drag effect of the foliage layer. The turbulent fluxes of trees ( and ) coming from the disaggregation of ISBA fluxes calculated with the bigleaf concept (see Eqs. 6 and 7) are assumed to be produced not at ground level but at the height of the foliage layer within the canyon. These fluxes have, therefore, to be vertically distributed in the TEB-SBL equations that is here parameterized according to a function of the foliage density contained in each k layer:
with dt(k) the foliage-layer thickness in the k layer. The leaf area index (LAI in m2 m−2) is prescribed as input data. The leaf area density (LAD in m2 m−3) is the vertical profile of LAI, which depends on the total thickness of the foliage layer and the form of tree crowns. For now, tree crowns are described as rectangular in shape so that LAD is constant over the thickness of the tree-foliage layer, i.e., between htk and ht that are the height of trunks and height of trees, respectively.
These turbulent fluxes are now included in the evolution equations of temperature (Eq. 12) and humidity (Eq. 13) profiles of TEB-SBL, in addition to ground-based contributions coming from natural soils and low-level vegetation:
with δt being the overlapping fraction of trees in the canyon and Vgrid the total air volume.
4.3 Aerodynamic effect of trees
The presence of trees also modifies the airflow within the canyon. To account for this, a supplementary drag term is now included in the evolution equations of momentum (Eq. 10) and turbulent kinetic energy (Eq. 11):
Numerous studies found in the literature (Cassiani et al., 2008; Dupont and Brunet, 2008; Aumond et al., 2013; Krayenhoff et al., 2015) propose an optimized value of the drag coefficient of trees (). Until the work of Katul et al. (1998), this coefficient is usually defined as a constant .
5.1 General principle
The UTCI calculation according to the polynomial regression equation proposed by Bröde et al. (2012) (not detailed here) requires four meteorological parameters: air temperature at 2 m above the ground, the water vapor pressure at the same level, the wind speed at 10 m above the ground, and the mean radiant temperature (Tmrt). This equation has been implemented in TEB (Kwok et al., 2019, Supplement) for calculating three UTCIs that are associated with a person (1) in the street exposed to the sun, (2) in the street in the shadow, and (3) in the building.
For outdoor conditions, in the case of a person in the sun, Tmrt is calculated by accounting for the ensemble of radiation sources received by the person, i.e., the direct and diffuse incoming short-wave radiation (S↓ and S⇓), the short-wave radiation after reflection on the walls, the road, and the ground-based natural covers in the canyon (, , ), the incoming atmospheric long-wave radiation (L↓), and the infrared emissions from the surrounding canyon surfaces (, , for walls, roads, and ground-based natural covers).
The direct short-wave radiation is assumed to be unidirectional and is weighted by a factor of projected area relative to the person (fp), which depends on sun elevation (γ in ∘) according to the formulation of Fanger (1970):
The other fluxes that are considered to be isotropic in TEB radiative calculations are weighted by the form factors calculated for the person (“b” index is used for “body”) in relation to the surrounding elements that contribute to radiation, i.e., Ψbs, Ψbr, and Ψbw for the sky, the road, and the walls, respectively (ground-based natural covers have the same form factor than road). Finally, the mean radiant temperature for the person in the sun is expressed according to the expression:
In this expression, the human body is characterized by a prescribed solar absorption coefficient (ab=0.70) and a prescribed emissivity (ϵb=0.97). In the case when the person is in the shadow, the term relative to direct short-wave radiation contribution is not taken into account so that the expression becomes:
5.2 Inclusion of tree effects
The new parameterization for trees in the TEB model requires us to adapt the radiative contributions in the UTCI calculations for outdoor conditions. First, the initial contributions from diffuse short-wave radiation and infrared radiation (detailed in Eq. 21) are corrected for the sky and the walls from the radiation attenuation effect through the tree foliage. These attenuation coefficients are those already presented in Redon et al. (2017) that are dependent on the leaf area density profile; they are referred to as τsr for attenuation between sky and road and τwr for attenuation between wall and road (see Eqs. B1–B4 in Redon et al., 2017).
In addition, the tree foliage contributes itself to the total infrared flux received by the person, due to is own infrared emission (a function of its temperature and its emissivity) and to the reemission of infrared radiation that it receives from the ground and walls. One can note that Redon et al. (2017) made the hypothesis that the short-wave radiation received by the tree foliage is only reemitted upward. As a result, no contribution from diffuse short-wave radiation from trees is involved in the mean radiant temperature calculation. The final expression for a person in the sun is as follows:
The infrared emission contribution due to the tree foliage is expressed as
with ϵt and Tt the emissivity and temperature of the tree foliage, respectively, and Ψtr the form factor for tree regarding emission coming from the road and ground-based natural covers.
An evaluation exercise of the TEB performances in simulating microclimatic conditions of an urban canyon with trees is performed for a real study case, i.e., the experimental campaign presented by Shashua-Bar et al. (2009). The TEB model here applied includes the ensemble of developments relative to urban trees: (1) the radiative processes detailed by Redon et al. (2017) and already evaluated by comparison with a reference model, (2) the energy exchanges between trees and air volume within the canyon, and (3) the aerodynamic effect of trees on local airflow. This version is referred to as TEB-Tree and is compared to the reference version of the model TEB-Ref (Lemonsu et al., 2012), which already integrated natural covers within the canyon but with a ground-based compartment.
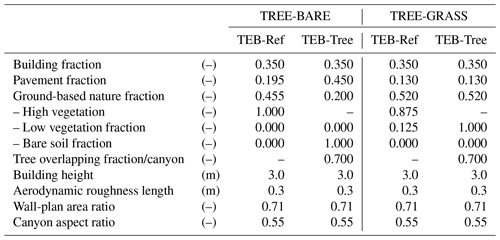
Table 1TEB input parameters according to the two configurations prescribed to represent the experimental site of Sde-Boqer according to the TEB-Ref and TEB-Tree versions (in accordance with Fig. 2).
6.1 Study area and experimental data
The experimental data have been collected on the campus of Sde-Boqer in the semidesert region of Negev of southern Israel (30.85∘ N, 34.78∘ E; 475 m of altitude) during summer 2007 (Shashua-Bar et al., 2009). Two semi-adjacent courtyards with comparable characteristics in terms of geometry and materials have been set up according to six landscape arrangements incorporating various combinations of bare soil, lawn, and trees. The cases here studied are the courtyard arranged with trees and bare ground and the one arranged with trees and grass, respectively referred to as TREE-BARE and TREE-GRASS according to Shashua-Bar et al. (2011). The trees are Prosopis juliflora and Tipuana tipu, which are common species for the region and are known to be water-consumption saving (Shashua-Bar et al., 2009). A drip irrigation was installed for each tree around the trunk. The lawn is Durban grass watered separately by sprinklers once in the morning.
The courtyards were equipped with sensors recording (1) air temperature, relative humidity, vapor pressure, and wind speed at 1.5 m above the ground; (2) radiation fluxes (incoming and outgoing radiation, and net radiation) at the roof top; (3) surface temperatures of eastern, western, and south-facing walls and tree foliage, as well as soil and pavement for TREE-BARE and grass for TREE-GRASS; and (4) transpiration from the trees using the sap flow method for both cases and evaporation from the grass with mini-lysimeters for TREE-GRASS. A meteorological station located 400 m northwest of the site in an open desert area recorded for the same period air temperature and humidity at 1.5 m above the ground, wind speed and direction at 10 m, as well as soil temperature.
6.2 Numerical configuration and experiments
The simulations are performed by running TEB on a single grid point to which are attributed the descriptive parameters of the experimented courtyards, considering that their configurations are close to the concept of urban canyon applied in TEB. The TEB model input parameters are prescribed according to the detailed description of the site proposed by Shashua-Bar et al. (2009). The semi-enclosed courtyard is oriented with an angle of 12∘ from the north (clockwise). The width is 5.5 m, and it is bordered by two rows of 3 m tall buildings with flat roofs. These buildings are made of light concrete; the pavement is also made of thin layers of light concrete laying on the ground. All impervious covers are light color with high albedo of 0.60 for walls and 0.40 for roofs and pavement. All thermal and radiative properties are listed in Table 1 in Lemonsu et al. (2012). For TREE-BARE, the ground inside of the courtyard consists of 70 % of pavement and 30 % of bare soil. The tree crowns present a overlapping rate of 70 % of ground-based surfaces. For TREE-GRASS, the tree coverage rate is unchanged, while 20 % of the ground is covered by pavement and 80 % by grass.
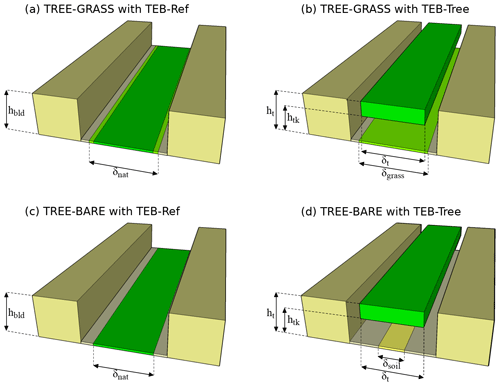
Figure 2Comparison of urban canyon characteristics prescribed by TEB-Ref (a, c) and TEB-Tree (b, d) versions for the experiments TREE-GRASS (a, b) and TREE-BARE (c, d).
The TEB input parameters derived from these real data differ depending on the version, TEB-Ref or TEB-Tree, that is used (see the description of configurations in Fig. 2 and Table 1). In the TEB-Ref standard approach, land cover fractions are calculated according to a single surface area without overlapping (as seen from the sky or by satellite). The sum of cover fractions is equal to 1. The tree cover has priority over the surfaces that are hidden, because they are located below, which is the case here since the tree-foliage layer covers 70 % of the canyon. In the TREE-BARE experiment, all bare ground and part of the pavement are therefore hidden by trees, which modifies the real fractions (Table 1). In the TREE-GRASS experiment, trees largely, but not totally, mask grass since the grass cover fraction is slightly greater than that of trees (Table 1). In comparison, the TEB-Tree version describes more realistically the arrangement of elements by dissociating the tree-foliage stratum from ground-based natural covers. As a consequence, for both experiments, the cover fractions prescribed for TEB are the real ones (Table 1), and their sum is greater than 1. As for morphological parameters, they remain the same as in the two experiments, i.e., a wall-plan area ratio of 0.71 and an aspect ratio of 0.55.
The meteorological forcing data that must be provided to TEB, i.e., air temperature, humidity, wind speed, incoming short- and long-wave radiation, and atmospheric pressure above the top of the canyon, are coming from in situ measurements collected above the roof and from data recorded by the reference meteorological station. The method is described in detail in Lemonsu et al. (2012).
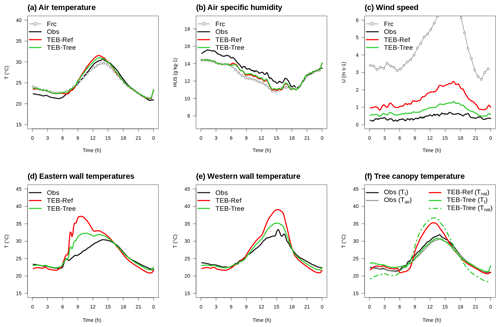
Figure 3Comparison of the TEB-Ref and TEB-Tree results (red and green lines, respectively) with meteorological variables (a–c) and surface temperatures of urban facets and trees (d–f) measured within the courtyard (black line). For air temperature, specific humidity and wind speed, the gray line with symbols indicates the forcing data above the buildings.
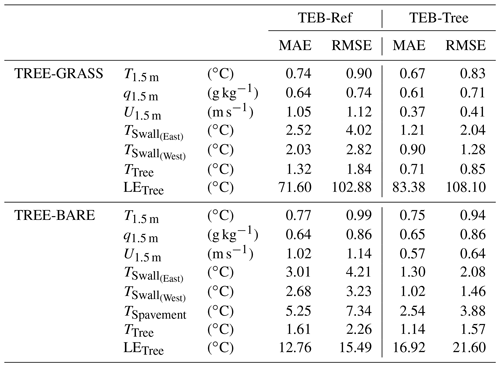
Table 2Mean absolute error (MBE; model minus observations, Obs) and root-mean-square error (RMSE) in temperature, humidity, wind speed at 1.5 m a.g.l., surface temperatures of walls and tree foliage, and in evaporation. The scores are calculated for TEB-Ref, TEB-Tree, and for the two courtyard configurations TREE-GRASS and TREE-BARE.
6.3 Results of evaluation
6.3.1 Microclimatic variables
The results obtained for the TREE-GRASS experiment are presented in detail here by comparing the modeled and measured diurnal cycles of the various parameters documented. They are complemented by the scores obtained for the TREE-BARE experiment. The comparison of microclimatic conditions and surface temperatures observed and simulated within the canyon indicates an improvement of simulation results with the new TEB-Tree version in comparison with TEB-Ref (Fig. 3). For air temperature, the improvement brought by TEB-Tree is noted for daytime hours: the simulated diurnal cycle is in better agreement with the observed one. In comparison, the TEB-Ref case indicates a too early warming in the morning. The statistical scores for the whole diurnal cycle (compiled in Table 2) are slightly better with a mean absolute error (MAE) and a root-mean-square error (RMSE) of 0.67 and 0.83 ∘C, respectively, instead 0.74 and 0.90 ∘C for TEB-Ref. For the TREE-BARE experiment, the improvement brought by TEB-Tree on air temperature modeling is confirmed by the statistical scores but remains quite low (Table 2). The simulation of the specific humidity is very slightly improved in the TREE-GRASS experiment, but both versions of the model give the same results for the TREE-BARE configuration. In the two experiments, whatever the model version, an overall underestimation of humidity is noted, whereas an increase during daytime could reasonably be expected in the new version, considering the latent heat flux from natural covers is now vertically distributed in TEB-Tree. A clear impact of the new parameterization is observed on wind. By considering the drag effect of tree foliage stratum in equations of TEB-SBL, the airflow is decelerated. The wind speed simulated in TEB-Tree is significantly lower than in TEB-Ref, i.e. conform more to measurements. MAE and RMSE are reduced from 1.05 and 1.12 m s−1, respectively, to 0.37 and 0.41 m s−1 for TREE-GRASS, and from 1.02 and 1.14 m s−1, respectively, to 0.57 and 0.64 m s−1 for TREE-BARE. Nonetheless, an overestimation of wind persists during the day.
6.3.2 Surface temperatures
The wall surface temperatures simulated in TREE-GRASS are significantly improved by taking into account the radiative effects of tree foliage (Fig. 3). The incoming radiation received by the canyon facets is reduced due to interception and attenuation by trees that are as tall as the buildings. As a result, the surface temperature maxima are lower in TEB-Tree than in TEB-Ref by 4–5 ∘C for eastern and western walls. Inversely at night, the tree foliage limits the cooling by trapping of infrared emission so that the surface temperatures are higher in TEB-Tree than TEB-Ref. Nonetheless, despite the improvement, TEB-Tree still overestimates the surface temperature, especially for the eastern wall in the morning. This suggests that the attenuation effect by tree foliage remains underestimated by the model in this case. The deviation from the measurement can also be explained by a difference between the compared quantities. The thermometer samples a specific area of the wall, while the model calculates an average temperature for the entire wall. The same improvement is noted in TREE-BARE, as well as for pavement temperature that was also measured during the experiment (Table 2).
6.3.3 Trees-related variables
TEB-Ref and TEB-Tree both calculate a composite temperature of natural covers (Tnat), which is compared here to the measured foliage temperature (Fig. 3f). The foliage presents a much lower diurnal temperature amplitude than that of Tnat, which is expected since Tnat includes a contribution of bare soil or grass depending on the experiment. The evolution of foliage temperature is much better captured by the tree temperature (Tt) diagnosed by TEB-Tree under the simple assumption that the foliage temperature is in equilibrium with the ambient temperature. The comparison between air temperature and foliage measurements confirms that this approximation is quite realistic. Finally, the measured evapotranspiration (combining tree transpiration and grass evaporation) is converted into latent heat flux (QE) and compared to model outputs (Fig. 4). Until noon, QE simulated by TEB-Ref is in good agreement with the observations. But QE decreases rapidly to zero in the afternoon, while the measured flux remains positive. TEB-Tree simulates a much higher QE during the day that persists up to 18:00 local time. Even if the day cycle is poorly reproduced in both cases, the daily water quantity evaporated is more realistic with TEB-Tree than with TEB-Ref, since the bias is less than 1 % instead of −42 % for TEB-Ref.
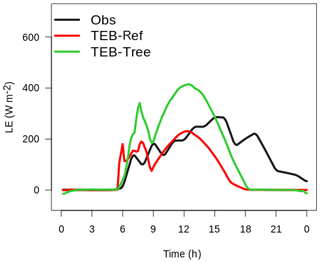
Figure 4Comparison of the TEB-Ref and TEB-Tree results (red and green lines, respectively) with the latent heat flux deduced from measurements of tree transpiration and grass evaporation (black line).
In the basis of this evaluation exercise, it can be concluded that the new developments provide improved model performance. The main improvements concern (1) the wall and ground surface temperatures that are much less overestimated than with the initial parameterization due to tree shading and (2) the wind, which is now slowed down by the presence of trees as observed. There is no very significant effect on air temperature or humidity, and it is difficult to conclude on the quality of the turbulent flux parameterization. The choice was made to keep the simple approach of the bigleaf parameterization for treating all natural covers as a composite compartment, rather than solve distinct energy budgets for soil, ground vegetation, and trees. This choice may be debatable, given that there are other models available today that can independently calculate water and energy flows between foliage and air. Nonetheless, in view of the results presented in the literature, it is difficult to objectively compare the performances of these models The main limitation remains the availability of experimental data allowing for a fine evaluation of the implemented processes, especially for turbulent flux calculation and impacts on air temperature and humidity (Lee and Park, 2008; Lee, 2011; Ryu et al., 2016). Besides, the comparisons presented by Ryu et al. (2016) do not show a very substantial change in the fluxes and Bowen ratio with the implementation of a specific tree parameterization.
6.4 Modeling of thermal comfort
An interest of this new parameterization for trees in urban canyons is to better predict outdoor thermal comfort conditions. The air temperature is not so different between the two experiments TEB-Ref and TEB-Tree. The modifications in radiation exchanges, energy fluxes, and ventilation induced by the presence of trees may have nonetheless a significant impact on heat perception by people. This is here quantified through the UTCI diagnosis, whose formulation has been adapted in TEB-Tree in order to include the radiation effects due to tree-foliage stratum as detailed in Sect. 5.2. Although we do not have any UTCI measurements for direct comparison, it is interesting to study how the two versions of TEB compare. In addition, the model results can be put into perspective with the study of Shashua-Bar et al. (2011), who investigated the influence of trees and grass on outdoor thermal comfort from the same experimental data.

Figure 5(a) Comparison of UTCI simulated in the courtyard by TEB-Ref (red line) and TEB-Tree (green line) for TREE-GRASS configuration; (b) comparison of UTCIs simulated by TEB-Tree for four different courtyard layouts.
6.4.1 Sensitivity of UTCI to the new TEB-Tree parameterization
The model calculates two separate UTCIs, i.e., in the sun and in the shadow. For the analysis of the results, they are averaged in a single UTCI according to the proportion of shade and sunlight in the courtyard. Since the model does not explicitly represent the spatial location of the elements in the canyon, but simply coverage fractions, these shade/sun fractions are calculated simply as the ratio between the direct solar radiation received by the ground surface and the direct incident solar radiation at the top of the canyon. TEB-Ref and TEB-Tree are compared in Fig. 5a for the TREE-GRASS configuration. Taking into account the foliage layer, TEB-Tree creates much more shade in the courtyard than TEB-Ref, which only represents the shade of buildings. Therefore, the UTCI simulated by TEB-Tree is lower during the day than that of TEB-Ref. This difference is 1.8 ∘C on average for the daytime hours and reaches 3 ∘C at maximum at 14:00 local time. For the present study case, it can be seen that the orders of magnitude of the differences in UTCI obtained by comparing the two versions, TEB-Ref and TEB-Tree, are very significant in terms of predicting heat stress. The TEB-Ref version simulates high heat stress conditions in the middle of the day, while TEB-Tree simulates UTCIs that do not exceed moderate heat stress conditions. Inversely, during the night, the infrared downward radiation emitted by the tree-foliage stratum in TEB-Tree (and potentially received by a person in the street) significantly limits the decrease in nocturnal UTCI. The UTCI remains on average 1.2 ∘C higher than in TEB-Ref simulations. This result highlights that street trees may degrade thermal comfort conditions at night by trapping radiation and amplifying downward infrared emissions inside the canyon while reducing ventilation.
6.4.2 Comparison of comfort conditions depending on courtyard layouts
Shashua-Bar et al. (2011, see Fig. 2) compared thermal conditions of the different courtyard layouts based on an index of thermal stress (expressed in W). This index was normalized to smooth the influence of variations in weather conditions from 1 d of measurement to the next. To get closer to these works, UTCIs simulated by TEB-Ref and TEB-Tree for the two configurations TREE-BARE and TREE-GRASS, but also for cases EXPOSED-BARE and EXPOSED-GRASS previously studied by Lemonsu et al. (2012), are compared. These two latter configurations are equivalent to TREE-BARE and TREE-GRASS in terms of ground properties but without trees. Identical weather conditions are applied for all courtyard layouts, using those of the TREE-GRASS experiment (Fig. 5b).
It can be seen that the case most exposed to heat stress during the day is the EXPOSED-BARE layout. Thanks to the evapotranspiration of lawn, the EXPOSED-GRASS layout allows for local cooling and slightly reduces the UTCI. The two configurations with trees are the most effective during the day: TREE-BARE improves comfort conditions mainly by increasing shade, while TREE-GRASS combines the benefits of shading and near-surface evapotranspiration. For the studied weather situation, only TREE-GRASS makes it possible to ensure moderate heat stress conditions within the courtyard. At night, the treeless configurations allow for a more significant lowering of UTCI than those with trees. As already mentioned previously, trees contribute to infrared radiation trapping and are themselves an additional source of radiation. On the other hand, their aerodynamic effect significantly reduces wind speed within the courtyard, which also contributes to limit the decrease in UTCI. These results are in agreement with those of Shashua-Bar et al. (2011, see Fig. 2). It is difficult to conclude on the realism of the orders of magnitude for the simulated UTCIs, since indices are not the same in the two studies and the method for comparison or normalization is also different. Nonetheless, whether for the day or night period, the same ranking between configurations in terms of impact on thermal comfort conditions is found. These results are not achievable with the TEB-Ref version, which simulates very similar comfort conditions regardless of the courtyard configuration (not shown).
The TEB model has evolved considerably in recent years, particularly with the objective of improving the representation of vegetation in urban areas. After the implementation of ground-based low vegetation inside the canyon, and of green roofs on buildings, an explicit representation of the tree-foliage layer was implemented. A detailed parameterization of associated radiative processes was developed and tested by Redon et al. (2017) with very encouraging results. The whole issue in this study was to treat the energy exchanges of vegetation by taking into account the dissociation of vegetation strata and to include the drag effect of trees on wind speed in the canyon.
The strategy is rather simple by maintaining the bigleaf approach for using the ISBA SVAT model, i.e., by calculating a single energy balance for natural covers, treated as a composite compartment. Nevertheless, the incident radiative fluxes provided to ISBA are calculated as a weighted average of those received by the natural ground surfaces and those received by the trees according to the coverage fractions. The energy fluxes calculated by ISBA are then redistributed according to the same principle between ground surfaces and trees, then injected into the SBL parameterization of TEB for the calculation of the air temperature and humidity vertical profiles in the canyon. Besides, a drag term of trees depending on the horizontal coverage fraction and the leaf density profile of trees is included in evolution equations of momentum and turbulent kinetic energy (TKE). It is in addition to the drag term already configured for buildings.
An evaluation exercise conducted in comparison to field measurements shows that, thanks to these new developments, the model better simulates surface temperatures and air temperature in the canyon. The main improvements concern (1) the wall and ground surface temperatures that are much less overestimated than with the initial parameterization due to tree shading and (2) the wind, which is now slowed down by the presence of trees as observed. There is no very significant effect on air temperature and humidity and it is difficult to conclude on the quality of the turbulent flux parameterization. In the future, it could be necessary to move towards a multi-energy budget (MEB) approach (Boone et al., 2017) to solve the energy balance separately from ground surfaces and trees. The bigleaf approach reveals limitations, and it raises conceptual questions about the choice of forcing level for energy flux calculations or the representativeness of a single temperature attributed to the composite layer of natural covers.
Finally, the UTCI diagnosis was reformulated by taking into account the presence of trees. This essentially consisted of adding infrared emissions from trees to the mean radiant temperature calculation. The other modifications presented here and in Redon et al. (2017) have also an influence on the UTCI, because they modify radiative exchanges and micrometeorological variables in the canyon, particularly wind. The results obtained by comparing different courtyard layouts with and without trees are in accordance with those of Shashua-Bar et al. (2011). The presence of trees improves thermal comfort conditions during the day because of shadow effects but degrades them during the night. Only the TEB-Tree version is able to correctly simulate these effects that was confirmed by an additional evaluation conducted for another study site in France (de Munck et al., 2018). This underlines the relevance of explicitly taking trees into account in urban climate models in order to more realistically model urban design strategies and impacts on thermal comfort.
The new developed code will be included in the next official version of SURFEX v9.0. It is currently a specific user library developed on the basis of the official version SURFEX v8.0. The whole code is available in the Supplement.
The model outputs and R programs to plot them are available in the Supplement. The experimental data that are used for the evaluation stage were provided by Evyatar Erell from Ben-Gurion University of the Negev. To access these data, it is necessary to contact Evyatar Erell directly.
The supplement related to this article is available online at: https://doi.org/10.5194/gmd-13-385-2020-supplement.
All three co-authors have contributed to the development and improvement of the TEB code in SURFEX V8.0. Besides, ER and AL performed the evaluation step by performing the simulation and comparing the model results with the experimental data.
We acknowledge Evyatar Erell from Ben-Gurion University of the Negev for giving us access to the experimental data.
This paper was edited by Leena Järvi and reviewed by two anonymous referees.
Abhijith, K., Kumar, P., Gallagher, J., McNabola, A., Baldauf, R., Pilla, F., Broderick, B., Sabatino, S. D., and Pulvirenti, B.: Air pollution abatement performances of green infrastructure in open road and built-up street canyon environments – A review, Atmos. Environ., 162, 71–86, https://doi.org/10.1016/j.atmosenv.2017.05.014, 2017. a
Alexander, P. J. and Mills, G.: Local Climate Classification and Dublin’s Urban Heat Island, Atmosphere, 5, 755–774, https://doi.org/10.3390/atmos5040755, 2014. a
Armson, D., Stringer, P., and Ennos, A.: The effect of tree shade and grass on surface and globe temperatures in an urban area, Urban For. Urban Gree., 11, 245–255, https://doi.org/10.1016/j.ufug.2012.05.002, 2012. a
Aumond, P., Masson, V., Lac, C., Gauvreau, B., Dupont, S., and Berengier, M.: Including the Drag Effects of Canopies: Real Case Large-Eddy Simulation Studies, Bound.-Lay. Meteorol., 146, 65–80, https://doi.org/10.1007/s10546-012-9758-x, 2013. a
Bernatzky, A.: The contribution of tress and green spaces to a town climate, Energ. Buildings, 5, 1–10, https://doi.org/10.1016/0378-7788(82)90022-6, 1982. a
Berry, R., Livesley, S., and Aye, L.: Tree canopy shade impacts on solar irradiance received by building walls and their surface temperature, Build. Environ., 69, 91–100, https://doi.org/10.1016/j.buildenv.2013.07.009, 2013. a
Best, M. J. and Grimmond, C. S. B.: Modeling the Partitioning of Turbulent Fluxes at Urban Sites with Varying Vegetation Cover, J. Hydrometeorol., 17, 2537–2553, https://doi.org/10.1175/JHM-D-15-0126.1, 2016. a
Boone, A., Samuelsson, P., Gollvik, S., Napoly, A., Jarlan, L., Brun, E., and Decharme, B.: The interactions between soil–biosphere–atmosphere land surface model with a multi-energy balance (ISBA-MEB) option in SURFEXv8 – Part 1: Model description, Geosci. Model Dev., 10, 843–872, https://doi.org/10.5194/gmd-10-843-2017, 2017. a
Bournez, H.: Etude du rôle de la végétation dans la création de microclimats urbains : approche combinée de mesures et de modélisations à différentes échelles, PhD thesis of Stasbourg University, France, 2018 (in French). a
Bouyer, J., Inard, C., and Musy, M.: Microclimatic coupling as a solution to improve building energy simulation in an urban context, Energ. Buildings, 43, 1549–1559, https://doi.org/10.1016/j.enbuild.2011.02.010, 2011. a
Bröde, P., Fiala, D., Błażejczyk, K., Holmér, I., Jendritzky, G., Kampmann, B., Tinz, B., and Havenith, G.: Deriving the operational procedure for the Universal Thermal Climate Index (UTCI), Int. J. Biometeorol., 56, 481–494, https://doi.org/10.1007/s00484-011-0454-1, 2012. a
Bruse, M.: ENVI-met 3.0: Updated Model Overview, Scientific documentation, available at: http://www.envi-met.net/documents/papers/overview30.pdf (last access: 20 January 2020), 2004. a
Bruse, M. and Fleer, H.: Simulating surface–plant–air interactions inside urban environments with a three dimensional numerical model, Environ. Model. Softw., 13, 373–384, https://doi.org/10.1016/S1364-8152(98)00042-5, 1998. a, b
Buccolieri, R., Salim, S., Leo, L., Di Sabatino, S., Chan, A., Ielpo, P., de Gennaro, G., and Gromke, C.: Analysis of local scale tree–atmosphere interaction on pollutant concentration in idealized street canyons and application to a real urban junction, Atmos. Environ., 45, 1702–1713, https://doi.org/10.1016/J.ATMOSENV.2010.12.058, 2011. a
Cassiani, M., Katul, G. G., and Albertson, J. D.: The Effects of Canopy Leaf Area Index on Airflow Across Forest Edges: Large-eddy Simulation and Analytical Results, Bound.-Lay. Meteorol., 126, 433–460, https://doi.org/10.1007/s10546-007-9242-1, 2008. a
Cuxart, J., Bougeault, P., and Redelsperger, J.-L.: A turbulence scheme allowing for mesoscale and large-eddy simulations, Q. J. Roy. Meteor. Soc., 126, 1–30, 2000. a
de Munck, C. S., Lemonsu, A., Bouzouidja, R., Masson, V., and Claverie, R.: The GREENROOF module (v7.3) for modelling green roof hydrological and energetic performances within TEB, Geosci. Model Dev., 6, 1941–1960, https://doi.org/10.5194/gmd-6-1941-2013, 2013. a
de Munck, C., Bernard, E., Lemonsu, A., Hidalgo, J., Touati, N., and Bouyer, J.: Impact of modelling vegetation at high resolution on urban climate variability, in: 10th International Conference on Urban Climate (ICUC10), New York City, US, 2018. a, b
Dupont, S. and Brunet, Y.: Edge Flow and Canopy Structure: A Large-Eddy Simulation Study, Bound.-Lay. Meteorol., 126, 51–71, https://doi.org/10.1007/s10546-007-9216-3, 2008. a
Fanger, P. O.: Thermal comfort : analysis and applications in environmental engineering, Copenhagen: Danish Technical Press, 1970. a
Fenner, D., Meier, F., Scherer, D., and Polze, A.: Spatial and temporal air temperature variability in Berlin, Germany, during the years 2001–2010, Urban Climate, 10, 308–331, https://doi.org/10.1016/j.uclim.2014.02.004, 2014. a
Gastellu-Etchegorry, J., Zagolski, F., and Romier, J.: A simple anisotropic reflectance model for homogeneous multilayer canopies, Remote Sens. Environ., 57, 22–38, 1996. a
Giometto, M., Christen, A., Egli, P., Schmid, M., Tooke, R., Coops, N., and Parlange, M.: Effects of trees on mean wind, turbulence and momentum exchange within and above a real urban environment, Adv. Water Resour., 106, 154–168, https://doi.org/10.1016/j.advwatres.2017.06.018, 2017. a
Grimmond, C., Souch, C., and Hubble, M.: Influence of tree cover on summertime surface energy balance fluxes, San Gabriel Valley, Los Angeles, Clim. Res., 6, 45–57, 1996. a
Hamdi, R. and Masson, V.: Inclusion of a Drag Approach in the Town Energy Balance (TEB) Scheme: Offline 1D Evaluation in a Street Canyon, J. Appl. Meteorol. Clim., 47, 2627–2644, https://doi.org/10.1175/2008JAMC1865.1, 2008. a
Heisler, G.: Urban form and climate change: Balancing adaptation and mitigation in the U.S. and Australia, ASHRAE Tran., 96, 1389–1396, 1990. a
Houet, T. and Pigeon, G.: Mapping urban climate zones and quantifying climate behaviors – An application on Toulouse urban area (France), Environ. Pollut., 159, 2180–2192, https://doi.org/10.1016/j.envpol.2010.12.027, 2011. a
Kastendeuch, P. P., Najjar, G., and Colin, J.: Thermo-radiative simulation of an urban district with LASER/F, Urban Climate, 21, 43–65, https://doi.org/10.1016/j.uclim.2017.05.003, 2017. a
Katul, G., Geron, C., Hsieh, C.-I., Vidakovic, B., and Guenther, A.: Active Turbulence and Scalar Transport near the Forest–Atmosphere Interface, J. Appl. Meteorol., 37, 1553–1546, 1998. a
Konarska, J., Uddling, J., Holmer, B., Lutz, M., Lindberg, F., Pleijel, H., and Thorsson, S.: Transpiration of urban trees and its cooling effect in a high latitude city, Int. J. Biometeorol., 60, 159–172, 2016. a
Krayenhoff, E., Christen, A., Martilli, A., and Oke, T.: A Multi-layer Radiation Model for Urban Neighbourhoods with Trees, Bound.-Lay. Meteorol., 151, 139–178, https://doi.org/10.1007/s10546-013-9883-1, 2014. a, b
Krayenhoff, E., Santiago, J.-L., Martilli, A., Christen, A., and Oke, T.: Parametrization of Drag and Turbulence for Urban Neighbourhoods with Trees, Bound.-Lay. Meteorol., 156, 157–189, https://doi.org/10.1007/s10546-015-0028-6, 2015. a, b
Kwok, Y., Schoetter, Lau, K.-L. L., Hidalgo, J., Ren, C., Pigeon, G., and Masson, V.: How does the local climate zone scheme discern the urban thermal environment? Evaluation for a European city (Toulouse) using numerical simulation data, Int. J. Climatol., 39, 5292–5315, 2019. a
Lee, S.: Further Development of the Vegetated Urban Canopy Model Including a Grass-Covered Surface Parametrization and Photosynthesis Effects, Bound.-Lay. Meteorol., 140, 315–342, 2011. a, b
Lee, S.-H. and Park, S.-U.: A Vegetated Urban Canopy Model for Meteorological and Environmental Modelling, Bound.-Lay. Meteorol., 126, 73–102, https://doi.org/10.1007/s10546-007-9221-6, 2008. a, b, c
Lemonsu, A., Masson, V., Shashua-Bar, L., Erell, E., and Pearlmutter, D.: Inclusion of vegetation in the Town Energy Balance model for modelling urban green areas, Geosci. Model Dev., 5, 1377–1393, https://doi.org/10.5194/gmd-5-1377-2012, 2012 a, b, c, d, e, f, g, h, i, j, k, l
Lindberg, F. and Grimmond, C. S. B.: The influence of vegetation and building morphology on shadow patterns and mean radiant temperatures in urban areas: model development and evaluation, Theor. Appl. Climatol., 105, 311–323, https://doi.org/10.1007/s00704-010-0382-8, 2011. a
Litvak, E. and Pataki, D.: Evapotranspiration of urban lawns in a semi-arid environment: An in situ evaluation of microclimatic conditions and watering recommendations, J. Arid Environ., 134, 87–96, https://doi.org/10.1016/j.jaridenv.2016.06.016, 2016. a
Malys, L., Musy, M., and Inard, C.: A hydrothermal model to assess the impact of green walls on urban microclimate and building energy consumption, Build. Environ., 73, 187–197, https://doi.org/10.1016/j.buildenv.2013.12.012, 2014. a
Martilli, A., Clappier, A., and Rotach, M.: An Urban Surface Exchange Parameterisation for Mesoscale Models, Bound.-Lay. Meteorol., 104, 261–304, https://doi.org/10.1023/A:1016099921195, 2002. a
Martini, A., Biondi, D., and Batista, A. C.: The microclimate of different landscape arrangements in street trees of Curitiba-pr State, Ciênc. Florest., 27, 1257–1268, 2017. a
Masson, V.: A Physically-Based Scheme For The Urban Energy Budget In Atmospheric Models, Bound.-Lay. Meteorol., 94, 357–397, https://doi.org/10.1023/A:1002463829265, 2000. a
Masson, V. and Seity, Y.: Including Atmospheric Layers in Vegetation and Urban Offline Surface Schemes, J. Appl. Meteorol. Climatol., 48, 1377–1397, https://doi.org/10.1175/2009JAMC1866.1, 2009. a
Miguet, F. and Groleau, D.: Urban bioclimatic indicators for urban planners with the software tool SOLENE, Portugal SB07 Sustainable Construction, materials and practices: challenges of the industry for the new millennium, Lisbon, Portugal, 348–355, 2007. a
Ndetto, E. and Matzarakis, A.: Urban atmospheric environment and human biometeorological studies in Dar es Salaam, Tanzania, Air Qual. Atmos. Hlth., 8, 175–191, https://doi.org/10.1007/s11869-014-0261-z, 2014. a
Noilhan, J. and Planton, S.: A Simple Parameterization of Land Surface Processes for Meteorological Models, Mon. Weather Rev., 117, 536–549, https://doi.org/10.1175/1520-0493(1989)117<0536:ASPOLS>2.0.CO;2, 1989. a
Offerle, B., Grimmond, C., Fortuniak, K., and Pawlak, W.: Intraurban Differences of Surface Energy Fluxes in a Central European City, J. Appl. Meteorol. Climatol., 45, 125–136, https://doi.org/10.1175/JAM2319.1, 2006. a
Oke, T.: The micrometeorology of the urban forest, Philos. T. R. Soc. B, 324, 335–349, https://doi.org/10.1098/rstb.1989.0051, 1989. a
Oke, T. R., Mills, G., Christen, A., and Voogt, J. A.: Urban Climates, Cambridge University Press, https://doi.org/10.1017/9781139016476, 2017. a
Peters, E., Hiller, R., and McFadden, J.: Seasonal contributions of vegetation types to suburban evapotranspiration, J. Geophys. Res.-Biogeosci., 116, G01003, https://doi.org/10.1029/2010JG001463, 2011. a
Potchter, O., Cohen, P., and Bitan, A.: Climatic behavior of various urban parks during hot and humid summer in the mediterranean city of Tel Aviv, Israel, Int. J. Climatol., 26, 1695–1711, https://doi.org/10.1002/joc.1330, 2006. a
Qiu, G.-Y., Li, H.-Y., Zhang, Q.-T., Chen, W., Liang, X.-J., and Li, X.-Z.: Effects of Evapotranspiration on Mitigation of Urban Temperature by Vegetation and Urban Agriculture, J. Integr. Agr., 12, 1307–1315, https://doi.org/10.1016/S2095-3119(13)60543-2, 2013. a
Redon, E. C., Lemonsu, A., Masson, V., Morille, B., and Musy, M.: Implementation of street trees within the solar radiative exchange parameterization of TEB in SURFEX v8.0, Geosci. Model Dev., 10, 385–411, https://doi.org/10.5194/gmd-10-385-2017, 2017. a, b, c, d, e, f, g, h, i, j
Ryu, Y., Bou-Zeid, E., Wang, Z., and Smith, J.: Realistic Representation of Trees in an Urban Canopy Model, Bound.-Lay. Meteorol., 159, 193–220, https://doi.org/10.1007/s10546-015-0120-y, 2016. a, b, c, d
Salim, M., Schlünzen, K., and Grawe, D.: Including trees in the numerical simulations of the wind flow in urban areas: Should we care?, J. Wind Eng. Ind. Aerod, 144, 84–95, https://doi.org/10.1016/j.jweia.2015.05.004, 2015. a
Santiago, J. and Martilli, A.: A Dynamic Urban Canopy Parameterization for Mesoscale Models Based on Computational Fluid Dynamics Reynolds-Averaged Navier–Stokes Microscale Simulations, Bound.-Lay. Meteorol., 137, 417–439, https://doi.org/10.1007/s10546-010-9538-4, 2010. a
Shashua-Bar, L. and Hoffman, M.: Vegetation as a climatic component in the design of an urban street: An empirical model for predicting the cooling effect of urban green areas with trees, Energ. Build., 31, 221–235, https://doi.org/10.1016/S0378-7788(99)00018-3, 2000. a
Shashua-Bar, L., Pearlmutter, D., and Erell, E.: The cooling efficiency of urban landscape strategies in a hot dry climate, Landscape Urban Plan., 92, 179–186, https://doi.org/10.1016/j.landurbplan.2009.04.005, 2009. a, b, c, d
Shashua-Bar, L., Pearlmutter, D., and Erell, E.: The influence of trees and grass on outdoor thermal comfort in a hot-arid environment, Int. J. Climatol., 31, 1498–1506, https://doi.org/10.1002/joc.2177, 2011. a, b, c, d, e, f
Souch, C.: The effect of trees on summertime below canopy urban climates: a case study, Bloomington, Indiana, J. Arboric., 19, 303–312, 1993. a
Wang, Z.-H., Bou-Zeid, E., and Smith, J. A.: A coupled energy transport and hydrological model for urban canopies evaluated using a wireless sensor network, Q. J. Roy. Meteor. Soc., 139, 1643–1657, https://doi.org/10.1002/qj.2032, 2013. a
Yamada, T.: A Numerical Model Study of Turbulent Airflow in and Above a Forest Canopy, J. Meteorol. Soc. Jpn., 60, 439–454, https://doi.org/10.2151/jmsj1965.60.1_439, 1982. a
- Abstract
- Introduction
- Representation of natural covers in TEB
- Surface energy balance of the canyon components in TEB
- Inclusion of trees in the surface boundary layer parameterization of TEB
- Parameterization of universal thermal climate index
- Evaluation of vegetated-canyon microclimate modeling under semiarid conditions
- Conclusions
- Code availability
- Data availability
- Author contributions
- Acknowledgements
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Representation of natural covers in TEB
- Surface energy balance of the canyon components in TEB
- Inclusion of trees in the surface boundary layer parameterization of TEB
- Parameterization of universal thermal climate index
- Evaluation of vegetated-canyon microclimate modeling under semiarid conditions
- Conclusions
- Code availability
- Data availability
- Author contributions
- Acknowledgements
- Review statement
- References
- Supplement





