the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An effective parameter optimization with radiation balance constraint in CAM5 (version 5.3)
Li Wu
Tao Zhang
Wei Xue
Uncertain parameters in physical parameterizations of general circulation models (GCMs) greatly impact model performance. In recent years, automatic parameter optimization has been introduced for tuning model performance of GCMs, but most of the optimization methods are unconstrained optimization methods under a given performance indicator. Therefore, the calibrated model may break through essential constraints that models have to keep, such as the radiation balance at the top of the model. The radiation balance is known for its importance in the conservation of model energy. In this study, an automated and efficient parameter optimization with the radiation balance constraint is presented and applied in the Community Atmospheric Model (CAM5) in terms of a synthesized performance metric using normalized mean square error of radiation, precipitation, relative humidity, and temperature. The tuned parameters are from the parameterization schemes of convection and cloud. The radiation constraint is defined as the absolute difference of the net longwave flux at the top of the model (FLNT) and the net solar flux at the top of the model (FSNT) of less than 1 W m−2. Results show that the synthesized performance under the optimal parameters is 6.3 % better than the control run (CNTL) and the radiation imbalance is as low as 0.1 W m−2. The proposed method provides an insight for physics-guided optimization, and it can be easily applied to optimization problems with other prerequisite constraints in GCMs.
The subgrid-scale physical processes in general circulation models (GCMs) are represented by parameterization schemes, which may exist with several uncertain parameters. Inappropriate parameters can seriously affect the overall performance of the model. The Intergovernmental Panel on Climate Change Fifth Assessment Report (IPCC AR5) pointed out that studies on parameter uncertainty are critical to improve climate simulation capabilities (Mastrandrea et al., 2011). Bauer et al. (2015) also indicated that small errors in the physical parameterization schemes could lead to large-scale systematic errors. Traditionally, to achieve better performance, the uncertain parameters are tuned based on the experience of model experts and statistical analysis. This is a labor-intensive job, and the tuning results make it difficult to achieve local or global optimality in complex climate models.
To efficiently reduce parameter-introduced uncertainty, quite a few automated parameter calibration methods have been proposed. These calibration methods can be categorized into two types. One attempts to obtain the probability distributions of the parameters by likelihood and Bayesian estimation methods. Cameron et al. (1999) exploited the generalized likelihood uncertain estimation to obtain parameter ranges with a specific confidence level. An adaptive Markov Chain Monte Carlo (MCMC) was used to calibrate the uncertain parameters in the fifth-generation atmospheric general circulation model (ECHAM5) (Järvinen et al., 2010). Edwards et al. (2011) proposed a simplified procedure of Bayesian calibration to make a quantification of uncertainty in climate forecasting. This type of method has also been successfully applied to the CAM3.1 model and the third Hadley Centre Climate Model (HadCM3) (Jackson et al., 2008; Williamson et al., 2013).
The other method is to adjust parameters using optimization methods to minimize the errors between model simulations and observations, which are formulated with a given performance indicator. Many intelligent evolutionary optimization algorithms were applied to model tuning. For example, both simulated stochastic approximation annealing (SSAA) (Yang et al., 2013) and multiple very fast simulated annealing (MVFSA) (Zou et al., 2014) were used for uncertainty quantification and parameter calibration.
Both methods can consider the interaction of parameters, achieve automatic optimization, and avoid the subjectivity and experientiality of manual calibration. However, they also share high computation cost challenges due to the hundreds and thousands of required simulations. This is usually unacceptable, especially for high-resolution climate models. To overcome the computational issues, the surrogate model, which is a way to replace the real climate model with a cheaper statistical model for faster optimization, has been recently introduced. Applications of these methods in climate models include the work presented by Neelin et al. (2010) and Wang et al. (2014). However, training a precise surrogate model for a complicated climate model such as the Community Earth System Model (CESM) is very challenging. Moreover, capturing the climatic characteristics of extreme events is difficult for the cheap statistical model. To make it possible to optimize parameters efficiently and quickly in the complex and highly nonlinear earth system models, an improved simplex algorithm was presented by Zhang et al. (2015). This method can overcome the shortcomings of the traditional simplex downhill method, and the computing efficiency of the algorithm is improved compared with evolutionary optimization algorithms.
The application of various automatic parameter optimization methods in climate models has gradually received more attention; however, the optimization algorithms mentioned above are mostly unconstrained, and they lack emphasis on the physical mechanisms of the model itself. This paper takes radiation balance as an example. According to the Earth's energy conservation theory, the absorbed solar radiation is approximately equal to outgoing longwave radiation at the top of the model. Forster et al. (2007) proposed that radiative balance is critical to the Earth's system, and the bias of radiation has a big impact on the change in surface temperature. Hourdin et al. (2017) pointed out that a 1 W m−2 change in global energy balance may result in a global mean surface temperature change of 0.5 to 1.5 K in coupled simulations. Additionally, Wild (2008) indicated that radiation biases in the GCMs may influence climate sensitivity, thus possibly distorting the prediction of future climate conditions. Lin et al. (2010) showed the importance of climate energy imbalance and stressed that long-term high-precision measurements of top of the atmosphere (TOA) radiation are necessary.
Radiation balance is critical for GCMs, but its deviation can still exceed 1 W m−2 in some CMIP5 models (Smith et al., 2015). To better understand this problem, many studies have tried to determine the cause of radiation deviation by analyzing the influence of uncertain parameters and making corresponding adjustments. Zhao et al. (2013) concluded that cloud microphysics and emission-related parameters have statistically important impacts on the global mean net radiation flux. Qian et al. (2015) indicated that net radiation flux is very sensitive to some parameters in cloud microphysics and convection. The improvement of the simulation performance of the climatology and variability based on the radiation balance is very meaningful. However, the constrained optimization methods used to calibrate parameters with physical constraints in climate models remain to be further studied. Cheng et al. (2018) showed that penalty functions and the separation of objective and constraint methods are popular for solving constrained problems. Penalty methods encourage the search toward feasible regions by increasing the objective function value with a penalty value for the points that violate the constraints. The exterior penalty method is relatively easy to implement, and it can be widely used in various algorithms. The separation of objective and constraint is commonly used by transforming constraints into objectives, but it is limited by the convergence of the multi-objective algorithms when the optimization problem has a high computational cost.
The purpose of this paper is to propose an effective constrained optimization method and demonstrate its feasibility in the calibration of uncertain parameters under the premise of ensuring the balance of radiation. This paper is organized as follows. Section 2 describes the details of the model and experimental design. Section 3 introduces the new constrained parameter calibration method. Evaluations and analysis of the optimization results are presented in Sect. 4. The last section contains the conclusion and discussion.
2.1 Model description
The model used in this study is CAM5 (release v5.3), which is the atmospheric component of the CESM 1.2.1. The dynamical core uses the finite-volume method developed by Lin and Rood (1996) and Lin (2004).
More details on CAM5 can be found in the work of Neale et al. (2010). Deep convection is handled by a parameterization scheme developed by Zhang and McFarlane (1995) with the further modifications of Richter and Rasch (2008), as well as Neale et al. (2008). The original parameterization of stratiform cloud microphysics is handled by Morrison and Gettelman (2008). Modifications of ice nucleation and ice supersaturation can be found in Gettelman et al. (2010). The parameterization of fractional stratiform condensation is described by Zhang et al. (2003) as well as Park et al. (2014). Radiation scheme uses the rapid radiative transfer method for GCMs (RRTMG) (Mlawer et al., 1997; Iacono et al., 2008).
2.2 Experiment design
Table 1 shows the parameters to be adjusted, the ranges, and the default values. These parameters were identified as sensitive to cloud and convection processes in previous studies. Qian et al. (2018) showed that deep-convection precipitation efficiency zmconv_c0_lnd and zmconv_ c0_ocn have significant impact on the variance of shortwave cloud forcing (SWCF) over the land and ocean, respectively. Thresholds of relative humidity for high and low stable clouds (cldfrc_rhminh and cldfrc_rhminl) are regarded as the important parameters for cloud and radiation (Zhang et al., 2018). In addition, the relative humidity threshold for low clouds is also one of the strongest parameters impacting the global mean precipitation, and it makes a huge contribution to the TOA net radiative fluxes in CAM5 (Qian et al., 2015). The timescale for the consumption rate of deep convective available potential energy (CAPE) (zmconv_tau) is identified as the most sensitive parameter to the convective precipitation in the Zhang–McFarlance scheme by Yang et al. (2013). The cloud ice sedimentation velocity (cldsed_ai) has a significant effect on cloud radiative forcing (Mitchell et al., 2008), and it has been identified as a high-impact parameter in sensitivity experiments related to temperature, radiation, and precipitation, etc. (Sanderson et al., 2008). The ranges of these parameters are based on previous studies (Qian et al., 2015; Zhang et al., 2018).
Table 2The output variables used to evaluate performance metric index and the source of the corresponding observations.

The output variables used to synthesize a performance indicator are longwave cloud forcing (LWCF), SWCF, precipitation (PRECT), humidity at 850 hPa (Q850), and temperature at 850 hPa (T850), shown in Table 2. The observations of LWCF and SWCF are from CERES-EBAF (Clouds and the Earth's Radiant Energy System-Energy Balanced and Filled; Loeb et al., 2014). PRECT is from GPCP (Global Precipitation Climatology Project; Adler et al., 2003), and Q850 and T850 are from ERA-Interim, which was produced by the ECMWF (Dee et al., 2011).
In this study, we use 1.9∘ latitude × 2.5∘ longitude resolution CAM5 with 30 vertical layers. Each simulation is a 5-year atmospheric model intercomparison project (AMIP) from 2000 to 2004 with the observed climatological sea surface temperature (SST) and sea ice (Rayner et al., 2003). The simulations in the last 3 years are used to evaluate the synthesized performance metric and constraint.
A constrained automatic optimization method is proposed based on Zhang et al. (2015). The synthesized metrics used to evaluate the performance of overall simulation skills are shown in Eq. (3):
represents a criterion for the simulation skill of the models with modified parameters; is an evaluation of the default experiment simulation skill. If the indicator χ2 is less than 1, this means that the simulation with tuned parameters is better than the control run (CNTL). The smaller the index, the better performance of model. The model outputs are represented by , and denotes the corresponding reanalysis or observation data. The expression represents model outputs from the CNTL. The weight of the different grids on the sphere is represented by ω. I denotes the total number of grids in the model. The number of the output variables in the performance index is represented by NF.
The radiation balance is defined as the absolute value of the difference between net solar flux (FSNT) and net longwave flux (FLNT) in climatology at the top of the model of less than 1 W m−2, which is the maximum deviation of radiation observations in the decade before 2014 (Trenberth et al., 2014).
Coupled with the radiation balance constraint, the optimization problem of this study can be expressed as Eqs. (4) and (5):
Converting the unconstrained problem into a constrained problem using the penalty function method, it can be transformed into the augmentation function as Eq. (6):
The penalty factor β for the constraint in Eq. (6) is chosen to be 10 000 if the constraint in Eq. (5) is not satisfied; otherwise it is equal to 0. The purpose of this choice is to optimize the search space to avoid the possibility of radiation imbalance. This penalty function method is easy and effective when dealing with this tightly constrained optimization.
We use the improved simplex downhill method, proposed by Zhang et al. (2015), to optimize the augment function. Firstly, the single-parameter perturbation sample method (SPP) is used to obtain several better initial values, while ensuring that the initial geometry of simplex downhill is well-conditioned. The initial value preprocessing mechanism ensures that the algorithm starts from a good basis. This is important for the simplex algorithm, which may easily fall into local optimum. Next, the simplex downhill algorithm is applied to search for better performance.
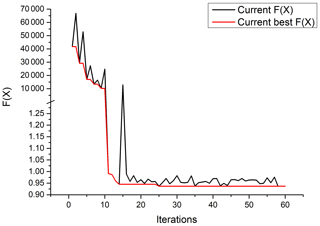
Figure 1The change in augmentation function F(x) across the optimization iterations. The x axis is the number of iterations. The y axis is the value of F(x) in Eq. (6). The black line shows the value of F(x) in a given iteration step, while the red line shows the best F(x) value up to the current iteration step.
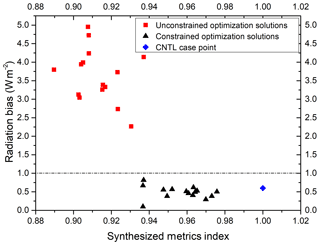
Figure 2Comparison of results between the constrained optimization algorithm and the unconstrained optimization algorithm. The 15 red squares and 15 black triangles are optimized solutions found by the unconstrained optimization algorithm and constrained algorithms, respectively. The blue diamond is the result of the CNTL experiment. The x axis is the synthesized metric index in Eq. (3). The y axis is the radiation bias at the top of the model.
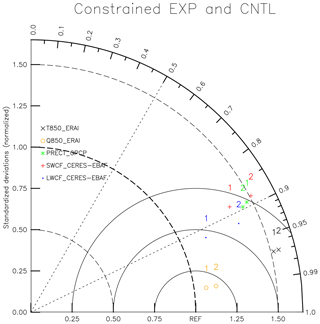
Figure 3Taylor diagram of the climate mean state of each output variable from 2002 to 2004 between the model run with optimal parameters and the CNTL run. The number (1) in the diagram stands for EXP, and (2) stands for CNTL.
F(x) gradually converges as shown in Fig. 1. There are some cases in which the radiation balance is not satisfied at the beginning of optimization. However, as the iteration step increases, the search space of the algorithm is constrained within the feasible range. The goal is then to make the synthesized performance metric smaller. In addition, a comparative experiment with unconstrained algorithms is done to verify our doubts about unconstrained methods. Figure 2 shows the performance indices and radiation deviations corresponding to the first 15 solutions after the two algorithms converge. The constrained optimization algorithm can find solutions that are more radiation-balanced; however, the final solution metrics are not as good as the unconstrained optimization algorithm. Compared to the CNTL experiment, we can find quite a few solutions with better metrics and smaller radiation biases.
4.1 The optimal model
The best uncertainty parameters obtained by the unconstrained optimization method optimize the overall performance of the simulation by 10.1 %, but they have a radiation deviation of up to 3.8 W m−2. When considering the converged constrained optimization algorithm, the optimal parameters can improve the model performance by 6.3 %, and the radiation imbalance is as low as 0.1 W m−2. The corresponding results of the optimal solutions with the two methods are shown in Table 3. Both unconstrained optimization and constrained optimization can further improve the simulation performance, but unconstrained optimization may encounter an optimal solution that does not satisfy the radiation balance, thus leading to meaningless optimization. The optimization results discussed below are based on the proposed constrained optimization method.
Table 3Synthesized performance metric index and radiation bias in the CNTL run and the optimal model run with unconstrained and constrained methods.

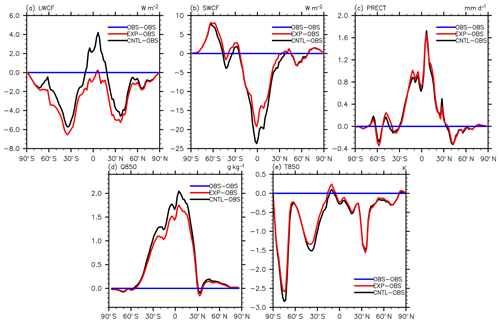
Figure 4Meridional distribution of the difference between EXP/CNTL and observed data of (a) LWCF, (b) SWCF, (c) PRECT, (d) Q850, and (e) T850. The position of the dark blue line is 0; the red and black solid lines represent the difference between EXP ∕ CNTL and the observations.
Table 4Performance metric index of each variable in the optimal model run with unconstrained and constrained methods.
The optimization of each output variable is shown in Table 4. In addition, a Taylor diagram is used to estimate the model performance through the standard deviation and correlation (Fig. 3). By combining the results of Table 4 and Fig. 3, it can be concluded that SWCF and Q850 receive most optimization, as they achieve a better performance index. Also, compared to the default experiment, their standard deviations have improved. Table 5 shows the standard deviations of the variables, which are important for the model but not used as evaluation criteria. It is noteworthy that they are also close to the default experiment.
Table 5The percentage of standard deviation of the eight fields between the CNTL run and the optimal model run with constrained optimization according to the corresponding observations.
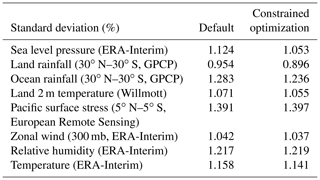
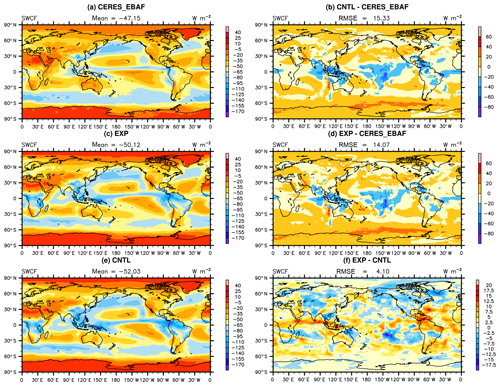
Figure 5The spatial distribution of TOA SW cloud forcing of (a) observation, (b) CNTL–observation, (c) EXP, (d) EXP–observation, (e) CNTL, and (f) EXP–CNTL.
For a more comprehensive analysis of the spatial variation of the output variables, the zonal distribution of the difference between the control (labeled as CNTL)/the optimized (labeled as EXP) simulations and observations of all metric variables are shown in Fig. 4. SWCF and Q850 have been obviously improved over low and middle latitudes, but the changes in PRECT and T850 are not particularly notable. Further, LWCF only showed significant improvement near the Equator, and it slightly deteriorated over the middle and high latitudes.
4.2 Interpretation of the results
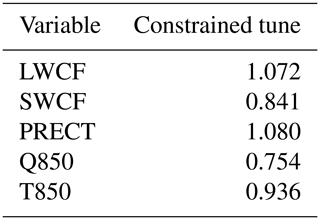
The optimized parameters values are provided in the “Constrained tune” column of Table 1. The deep-convection precipitation efficiency over land and ocean is reduced relative to the default values. The timescale for the consumption rate of CAPE for deep convection is smaller than the default value, and both relative humidity thresholds for high and low clouds are increased. Additionally, the sedimentation velocity of cloud ice is larger. Next, we will explain how the changes in these parameters are related to the results of the simulations.
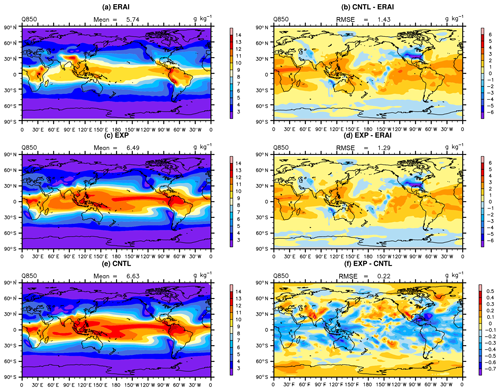
Figure 6The spatial distribution of specific humidity at 850 hPa of (a) observation, (b) CNTL–observation, (c) EXP, (d) EXP–observation, (e) CNTL, and (f) EXP–CNTL.
The relative humidity threshold for low clouds is larger in optimization experiments than the default value, which will obviously lead to the decrease in low-cloud fraction. The decreased low-cloud fraction is consistent with the increase in SWCF. The CNTL experiment has excelled at simulating the spatial distribution of SWCF (Fig. 5c), but it has a negative bias over the ocean in the low latitudes, where the improvement is significant in the optimal experiment.
The zonal mean specific humidity at 850 hPa is significantly improved, and its spatial distribution is presented in Fig. 6. In the optimal experiment, the atmosphere is drier in the tropics and middle latitudes, which is closer to the observation than the CNTL experiment. Meanwhile, the middle to low troposphere is also slightly drier in these areas (Fig. 7), which may be related to the increased convective precipitation. A quasi-equilibrium closure is used in the deep-convection scheme in CAM5, which is based on CAPE. The adjustment timescale represents the denominator of the cloud bottom convective mass flux. When the timescale is shorter with less changed CAPE, the increased cloud-base mass flux would help to enhance the convective precipitation. Additionally, compared to the CNTL experiment, the lower troposphere gets warmer and the middle troposphere is colder, which exacerbates the instability of the temperature structure (Fig. 8) and leads to more convective precipitation. The spatial distribution of convective precipitation over the tropics where convection occurs most frequently can be seen in Fig. 9. The increase in convective precipitation may be related to the decrease in specific humidity at 850 hPa. However, the increase in total precipitation is not particularly significant and is dominated by the changes in convective precipitation. The main reason is likely associated with the decreased precipitation efficiency parameters, which could reduce the convective precipitation as compensation. Therefore, the decreases in precipitation efficiency partially offset the precipitation change caused by tau and temperature structure.
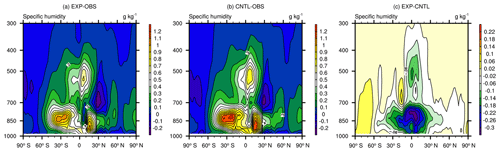
Figure 7Pressure–latitude distributions of specific humidity of (a) EXP–OBS, (b) CNTL–OBS, and (c) EXP–CNTL.
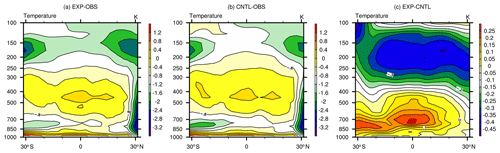
Figure 8Pressure–latitude distributions of temperature of (a) EXP–OBS, (b) CNTL–OBS, and (c) EXP–CNTL.
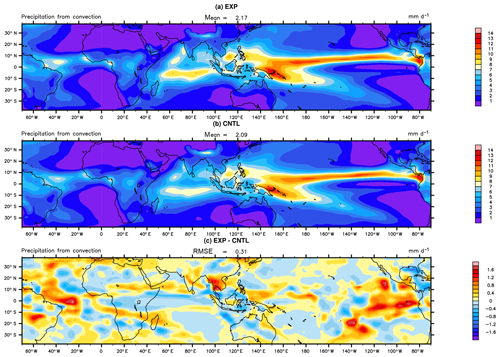
Figure 9The spatial distribution of convective precipitation over the tropics of EXP (a), CNTL (b), and EXP–CNTL (c).
It is difficult for all variables to be optimized, due to the strong interaction among parameters and the complex relationship among output variables. The simulations of T850 between optimal and CNTL experiments are very similar. It is likely the result of the combined effects of all relevant parameterizations. In the optimal experiment, LWCF is closer to the observation in the tropics, but it becomes slightly smaller at middle to high latitudes compared to the CNTL experiment, which implies the larger bias. The relative humidity threshold for high clouds and the sedimentation velocity of ice crystals are correspondingly increased, and both of them would lead to the reduction in high clouds. High-cloud fraction changes compared to the CNTL experiment can be seen in Fig. 10c. The reduced high cloud is consistent with the reduction in LWCF. Cloud changes also inevitably affect SWCF. It can be seen that the middle cloud has increased relative to the default experiment (Fig. 10c), and the increase in the middle cloud may be related to the decrease in precipitation efficiency over the ocean.
Note that three of six parameters hit their lowest allowable limit with the TOA balance constraint. We found that the incoming shortwave radiation flux is more sensitive to tuning parameters than the outgoing longwave radiation flux. Thus, to reduce the TOA imbalance and keep the reasonable model performance, the shortwave radiation flux should be reduced largely via increasing low-cloud fraction and liquid water content. These three variables can help achieve this by setting to the lowest bounds. This suggests that getting both the TOA balance and reasonable model performance is a relatively complex and difficult problem due to model structure problems, as pointed out by Qian et al. (2018) and Yang et al. (2019). Meanwhile, finding out how to pick parameters with a similar sensitivity to both longwave and shortwave radiation flux might be a potential approach to overcome the bound limit and it warrants further studies.
In conclusion, the increase in SWCF is consistent with the decrease in cloud fraction for the sake of a larger relative humidity threshold of low clouds. Changes in the Q850 are related to increased convective precipitation. Precipitation only slightly increases in the tropics, and the global total precipitation has changed very little, which is related to the comprehensive effect of the changes in the convection adjustment timescale, the precipitation efficiency parameter, and the vertical temperature structure. T850 simulated by the optimization experiment is similar to the default experiment. The reduced LWCF is related to the decreased high clouds caused by the increased relative humidity threshold for high clouds and the increased sedimentation velocity of ice crystals.
Radiation balance is a crucial factor for the long-term energy balance of GCMs, but it has not received enough attention in automatic parameter optimization. First of all, this paper points out that the previous parameter optimization algorithms do not consider radiation balance a necessary condition, and the obtained optimization parameters are likely to break this important physical constraint, which may lead to unacceptable calibrated parameters. Thus we propose an efficient constrained automatic optimization algorithm to calibrate the uncertainty parameters in CAM5 with the constraint of the absolute value of the difference of net solar flux and net longwave flux at the top of the model (less than 1 W m−2). In the parameter calibration, we use the comprehensive performance with the five fields of LWCF, SWCF, PRECT, Q850, and T850 as the performance indicators. We choose the uncertain parameters in cloud and convection parameterizations, including the deep-convection precipitation efficiency over land and ocean, thresholds of relative humidity for stable high and low clouds, the timescale for consumption rate deep CAPE, and the ice falling speed. Each simulation in our optimization experiments is a 5-year AMIP experiment forced with prescribed seasonal climatology of SST and sea ice.
The optimal parameters found by our method can increase the overall performance of the model by 6.3 %, and the radiation imbalance is as low as 0.1 W m−2. The most optimized variables are SWCF and Q850. The increase in SWCF is consistent with the decrease in cloud water due to a larger relative humidity threshold value for low clouds. The reduction in the Q850 in the troposphere may be related to the increase in convective precipitation. The change in global total precipitation is not particularly obvious, which is likely the comprehensive effect of the changes in the convection adjustment timescale, the precipitation efficiency parameter, and the structure of temperature over the troposphere. The change in T850 is very small, and the result is slightly better than that of the default experiment. Meanwhile, under the constraint of energy balance, LWCF has deteriorated in the middle and high latitudes. This also reflects some issues that may exist in the structure of the model.
The unconstrained optimization methods calibrate the uncertain parameters in climate models without a consideration of the principles that model have to hold, this creates challenges in maintaining the physics constraints and improving the structure of models. Perhaps a more physics-guided optimization is a better way to understand the principles of climate systems and to best use these principles in tuning processes. In the future, we will apply this method to coupled models, where the radiation imbalance has a more significant impact on long-term simulation stability. In addition, we will also try to introduce more constraints, such as the surface energy balance, into automatic parameter calibration.
The code of our algorithm, the observations, and the related scripts can be found at https://doi.org/10.5281/zenodo.3405619 (Wu, 2019). The source code of CAM5.3 is available from http://www.cesm.ucar.edu/models/cesm1.2/ (last access: 14 December 2019, NCAR, 2018). If you have any problems, please feel free to contact us (wulitianyi@gmail.com).
LW and TZ proposed the tuning method. LW, YQ, and WX designed the metrics and the constraint. YQ and LW evaluated the optimal results. LW, TZ, WX, and YQ wrote the paper.
The authors declare that they have no conflict of interest.
This work is partially supported by the National Key R&D Program of China (grant nos. 2017YFA0604500 and 2016YFA0602100) and the Center for High Performance Computing and System Simulation of Pilot National Laboratory for Marine Science and Technology (Qingdao).
This work is partially supported by the National Key R&D Program of China (grant nos. 2017YFA0604500 and 2016YFA0602100) and the Center for High Performance Computing and System Simulation of Pilot National Laboratory for Marine Science and Technology (Qingdao).
This paper was edited by Andrea Stenke and reviewed by two anonymous referees.
Adler, R. F., Huffman, G. J., Chang, A., Ferraro, R., Xie, P. P., Janowiak, J., and Gruber, A.: The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present), J. Hydrol., 4, 1147–1167, 2003.
Bauer, P., Thorpe, A., and Brunet, G.: The quiet revolution of numerical weather prediction, Nature, 525, 47–55, 2015.
Cameron, D., Beven, K. J., Tawn, J., Blazkova, S., and Naden, P.: Flood frequency estimation by continuous simulation for a gauged upland catchment (with uncertainty), J. Hydrol., 219, 169–187, 1999.
Cheng, G. H., Gjernes, T., and Wang, G. G.: An Adaptive Aggregation-Based Approach for Expensively Constrained Black-Box Optimization Problems, J. Mech. Design., 140, 091402, https://doi.org/10.1115/1.4040485, 2018.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., and Bechtold, P.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, 2011.
Edwards, N. R., Cameron, D., and Rougier, J.: Precalibrating an intermediate complexity climate model, Clim. Dynam., 37, 1469–1482, 2011.
Forster, P., Ramaswamy, V., Artaxo, P., Berntsen, T., Betts, R., Fa- hey, D. W., Haywood, J., Lean, J., Lowe, D. C., Myhre, G., Nganga, J., Prinn, R., Raga, G., Schulz, M., and Van Dorland, R.: Radiative Forcing of Climate Change, in Climate Change 2007 – The Physical Science Basis: Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, UK, 129–234, 2007.
Gettelman, A., Liu, X., Ghan, S. J., Morrison, H., Park, S., Conley, A., Klein,S. A., Boyle, J., Mitchell, D., and Li, J.-L.: Global simulations of ice nucle-ation and ice supersaturation with an improved cloud scheme in the Com-munity Atmosphere Model, J. Geophys. Res.-Atmos., 115, D18216, https://doi.org/10.1029/2009JD013797, 2010.
Hourdin, F., Mauritsen, T., Gettelman, A., Golaz, J. C., Balaji, V., Duan, Q., Folini, D., Ji, D., Klocke, D., Qian, Y., Rauser, F., Rio, C., Tomassini, L., Watanabe, M., and Williamson, D.: The art and science of climate model tuning, B. Am. Meteorol. Soc., 98, 589–602, 2017.
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res.-Atmos., 113, D13103, https://doi.org/10.1029/2008JD009944, 2008.
Jackson, C. S., Sen, M. K., Huerta, G., Deng, Y., and Bowman, K. P.: Error reduction and convergence in climate prediction, J. Climate, 21, 6698–6709, 2008.
Järvinen, H., Räisänen, P., Laine, M., Tamminen, J., Ilin, A., Oja, E., Solonen, A., and Haario, H.: Estimation of ECHAM5 climate model closure parameters with adaptive MCMC, Atmos. Chem. Phys., 10, 9993–10002, https://doi.org/10.5194/acp-10-9993-2010, 2010.
Lin, B., Chambers, L., P. Stackhouse Jr., Wielicki, B., Hu, Y., Minnis, P., Loeb, N., Sun, W., Potter, G., Min, Q., Schuster, G., and Fan, T.-F.: Estimations of climate sensitivity based on top-of-atmosphere radiation imbalance, Atmos. Chem. Phys., 10, 1923–1930, https://doi.org/10.5194/acp-10-1923-2010, 2010.
Lin, S.-J.: A “vertically Lagrangian” finite-volume dynamical core for global models, Mon. Weather Rev., 132, 2293–2307, 2004.
Lin, S.-J. and Rood, R. B.: Multidimensional flux-form semi-Lagrangian transport schemes, Mon. Weather Rev., 124, 2046–2070, 1996.
Loeb, N. and National Center for Atmospheric Research Staff (Eds.): The Climate Data Guide: CERES EBAF: Clouds and Earth’s Radiant Energy Systems (CERES) Energy Balanced and Filled (EBAF), available at: https://climatedataguide.ucar.edu/climate-data/ceres-ebafcloudsand-earths-radiant-energy-systems-ceres-energybalanced-andfilled, last access: 14 December 2019.
Mastrandrea, M. D., Mach, K. J., Plattner, G. K., Edenhofer, O., Stocker, T. F., Field, C. B., Ebi, K. L., and Matschoss, P. R.: The IPCC AR5 guidance note on consistent treatment of uncertainties: a common approach across the working groups, Clim. Change, 108, 675, 2011.
Mitchell, D. L., Rasch, P., Ivanova, D., McFarquhar, G., and Nousiainen, T.: Impact of small ice crystal assumptions on ice sedi- mentation rates in cirrus clouds and GCM simulations, Geophys. Res. Lett., 35, L09806, https://doi.org/10.1029/2008GL033552, 2008.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res.-Atmos., 102, 16663–16682, 1997.
Morrison, H. and Gettelman, A.: A new two-moment bulk stratiform cloud microphysics scheme in the community atmosphere model, version 3 (CAM3). Part I: Description and numerical tests, J. Climate, 21, 3642–3659, https://doi.org/10.1175/2008jcli2105.1, 2008.
NCAR: CESM1.2 SERIES PUBLIC RELEASE, available at: http://www.cesm.ucar.edu/models/cesm1.2/, last access: 14 December 2018.
Neale, R. B., Richter, J. H., Conley, A. J., Park, S., Lauritzen, P. H., Gettelman, A., Williamson, D. L., Rasch, P. J., Vavrus, S. J., Taylor, M. A., Collins, W. D., Zhang, M., and Lin, S. J.: Description of the NCAR Community Atmosphere Model (CAM5.0), Technical Report NCAR/TN-486+STR, National Center for Atmospheric Research, Boulder, CO, USA, 2010.
Neelin, J. D., Bracco, A., Luo, H., McWilliams, J. C., and Meyerson, J. E.: Considerations for parameter optimization and sensitivity in climate models, P. Natl. Acad. Sci. USA, 107, 21349–21354, 2010.
Park, S., Bretherton, C. S., and Rasch, P. J.: Integrating cloud processes in the Community Atmosphere Model, version 5, J. Climate, 27, 6821–6856, 2014.
Qian, Y., Wan, H., Yang, B., Golaz, J. C., Harrop, B., Hou, Z., Larson, V. E., Leung, L, R., Lin, G., Lin, W., Ma, P. L., Ma, H. Y., Rasch, P., Singh, B., Wang, H., Xie, S., Zhang, K.: Parametric Sensitivity and Uncertainty Quantification in the Version 1 of E3SM Atmosphere Model Based on Short Perturbed Parameter Ensemble Simulations, J. Geophys. Res.-Atmos., 123, 13046–13073, 2018.
Qian, Y., Yan, H., Hou, Z., Johannesson, G., Klein, S., Lucas, D., Neale, R., Rasch, P., Swiler, L., Tannahill, J., and Wang, H.: Parametric sensitivity analysis of precipitation at global and local scales in the Community Atmosphere Model CAM5, J. Adv. Model. Earth Sy., 7, 382–411, 2015.
Rayner, N., Parker, D. E., Horton, E., Folland, C., Alexander, L., Rowell, D., Kent, E., and Kaplan, A.: Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century, J. Geophys. Res.-Atmos., 108, 1871–2000, 2003.
Richter, J. H. and Rasch, P. J.: Effects of convective momentum transport on the atmospheric circulation in the community atmosphere model, version 3, J. Climate, 21, 1487–1499, https://doi.org/10.1175/2007jcli1789.1, 2008.
Sanderson, B. M., Piani, C., Ingram, W. J., Stone, D. A., and Allen, M. R.: Towards constraining climate sensitivity by linear analysis of feedback patterns in thousands of perturbed-physics GCM simulations, Clim. Dynam., 30, 175–190, 2008.
Smith, D. M., Allan, R. P., Coward, A. C., Eade, R., Hyder, P., Liu, C., Loeb, N. G., Palmer, M. D., Roberts, C.D., and Scaife, A. A.: Earth's energy imbalance since 1960 in observations and CMIP5 models, Geophys. Res. Lett., 42, 1205–1213, 2015.
Trenberth, K. E., Fasullo, J. T. and Balmaseda, M. A.: Earth's energy imbalance, J. Climate, 27, 3129–3144, 2014.
Wang, C., Duan, Q., Gong, W., Ye, A., Di, Z., and Miao, C.: An evaluation of adaptive surrogate modeling based optimization with two benchmark problems, Environ. Model. Softw., 60, 167–179, 2014.
Wild, M.: Short-wave and long-wave surface radiation budgets in GCMs: a review based on the IPCC-AR4/CMIP3 models, Tellus A., 60, 932–945, 2008.
Williamson, D., Goldstein, M., Allison, L., Blaker, A., Challenor, P., Jackson, L., and Yamazaki, K.: History matching for exploring and reducing climate model parameter space using observations and a large perturbed physics ensemble, Clim. Dynam., 41, 1703–1729, https://doi.org/10.1007/s00382-013-1896-4, 2013.
Wu, L.: Constrained-tuning-in-CAM5 v1.0.0 (Version v1.0.0), Zenod, https://doi.org/10.5281/zenodo.3405619, 2019.
Yang, B., Qian, Y., Lin, G., Leung, L. R., Rasch, P. J., Zhang, G. J., McFarlane, S. A., Zhao, C., Zhang, Y., Wang, H., Wang, M., and Liu, X.: Uncertainty quantification and parameter tuning in the CAM5 Zhang-McFarlane convection scheme and impact of improved convection on the global circulation and climate, J. Geophys. Res.–Atmos., 118, 395–415, 2013.
Yang, B., Berg, L. K., Qian, Y., Wang, C., Hou, Z., Liu, Y., and Pekour, M. S.: Parametric and Structural Sensitivities of Turbine Height Wind Speeds in the Boundary Layer Parameterizations in the Weather Research and Forecasting Model, J. Geophys. Res.-Atmos., 124, 5951–5969, 2019.
Zhang, G. J. and McFarlane, N. A.: Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian Climate Centre general circulation model, Atmos. Ocean, 33, 407–446, 1995.
Zhang, M., Lin, W., Bretherton, C. S., Hack, J. J., and Rasch, P. J.: A modified formulation of fractional stratiform condensation rate in the NCAR Community Atmospheric Model (CAM2), J. Geophys. Res.-Atmos., 108, 4035, https://doi.org/10.1029/2002JD002523, 2003.
Zhang, T., Li, L., Lin, Y., Xue, W., Xie, F., Xu, H., and Huang, X.: An automatic and effective parameter optimization method for model tuning, Geosci. Model Dev., 8, 3579–3591, https://doi.org/10.5194/gmd-8-3579-2015, 2015.
Zhang, T., Zhang, M., Lin, W., Lin, Y., Xue, W., Yu, H., He, J., Xin, X., Ma, H.-Y., Xie, S., and Zheng, W.: Automatic tuning of the Community Atmospheric Model (CAM5) by using short-term hindcasts with an improved downhill simplex optimization method, Geosci. Model Dev., 11, 5189–5201, https://doi.org/10.5194/gmd-11-5189-2018, 2018.
Zhao, C., Liu, X., Qian, Y., Yoon, J., Hou, Z., Lin, G., McFarlane, S., Wang, H., Yang, B., Ma, P.-L., Yan, H., and Bao, J.: A sensitivity study of radiative fluxes at the top of atmosphere to cloud-microphysics and aerosol parameters in the community atmosphere model CAM5, Atmos. Chem. Phys., 13, 10969–10987, https://doi.org/10.5194/acp-13-10969-2013, 2013.
Zou, L., Qian, Y., Zhou, T., and Yang, B.: Parameter tuning and calibration of RegCM3 with MIT–Emanuel cumulus parameterization scheme over CORDEX East Asia domain, J. Climate, 27, 7687–7701, 2014.